Вибіркове середнє квадратичне відхилення:
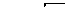 . (8.6.7)
. (8.6.7)
Приклад 8.6.1 У результаті тестування група з 25 чоловік набрала бали: 3, 2, 4, 3, 2, 2, 5, 3, 3, 2, 4, 2, 3, 5, 4, 2, 2, 3, 3, 3, 4, 2, 2, 3, 4.
а) Скласти таблицю розподілу частот і відносних частот.
б) Побудувати полігон частот.
в) Знайти емпіричну функцію й побудувати її графік.
г) Обчислити числові характеристики  .
.
Розв’язання. Проранжуємо вихідний ряд:
2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5.
а) Об'єм вибірки n = 25. Підрахуємо частоти 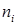 , частості
, частості  варіант
варіант 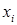 . Складемо таблицю розподілу:
. Складемо таблицю розподілу:
| xi | 2 | 3 | 4 | 5 |
| ni | 9 | 9 | 5 | 2 |
| wi | 0,36 | 0,36 | 0,2 | 0,08 |
Перевірка (згідно (8.6.1)): 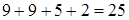 ,
,  .
.
б) Побудуємо полігон частот:
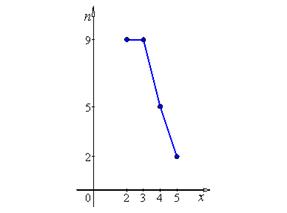
Рис. 8.6.1 – Полігон частот
в) Емпірична функція варіаційного ряду будується аналогічно інтегральній функції розподілу дискретної випадкової величини (приклад 8.2.1 в); замість ймовірностей  беремо відносні частоти
беремо відносні частоти  ). Одержимо:
). Одержимо:
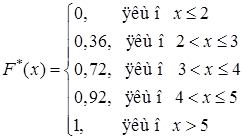
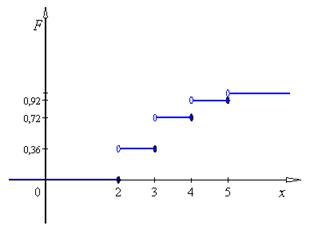
Рис. 8.6.2 – Графік емпіричної функції
г) Обчислимо числові характеристики  . Вибіркове середнє за формулою (8.6.3):
. Вибіркове середнє за формулою (8.6.3): 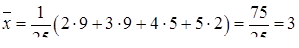 , дисперсія
, дисперсія 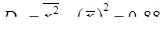 , де
, де 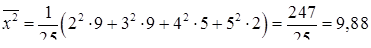 (за формулами (8.6.6)). Об'єм вибірки
(за формулами (8.6.6)). Об'єм вибірки 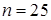 є непарним числом, тому медіана згідно (8.6.4)
є непарним числом, тому медіана згідно (8.6.4)  (13-те значення в ранжованому ряду). Найбільша частота
(13-те значення в ранжованому ряду). Найбільша частота 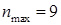 відповідає двом варіантам, значить, варіаційний ряд є двомодальным й мода
відповідає двом варіантам, значить, варіаційний ряд є двомодальным й мода 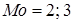 . Розмах за формулою (8.6.5)
. Розмах за формулою (8.6.5)  .
.
Література: [4, с. 606 – 616], [18], [21].
КОНТРОЛЬНА РОБОТА № 1
Модуль 1. Системи рівнянь, вектори та аналітична геометрія
|
|
|
1.1. Розв’язати систему лінійних рівнянь методами:
· оберненої матриці,
· Крамера,
· Гаусса.
1.1.1. 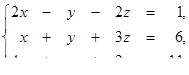
| 1.1.2. 
| 1.1.3. 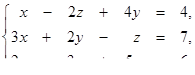
|
1.1.4. 
| 1.1.5. 
| 1.1.6. 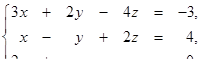
|
1.1.7. 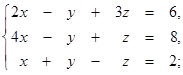
| 1.1.8. 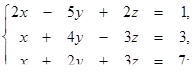
| 1.1.9. 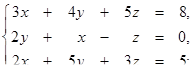
|
1.1.10. 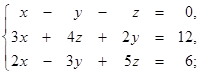
| 1.1.11. 
| 1.1.12. 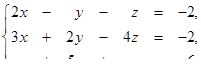
|
1.1.13. 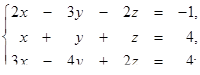
| 1.1.14. 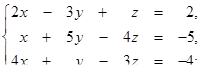
| 1.1.15. 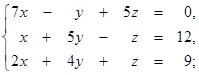
|
1.1.16. 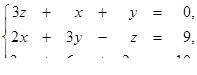
| 1.1.17. 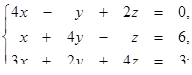
| 1.1.18. 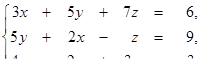
|
1.1.19. 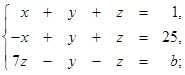
| 1.1.20. 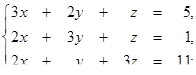
| 1.1.21. 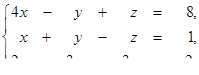
|
1.1.22. 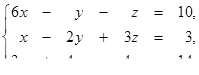
| 1.1.23. 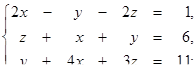
| 1.1.24. 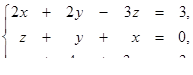
|
1.1.25. 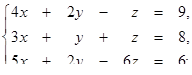
| 1.1.26. 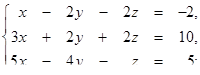
| 1.1.27. 
|
1.1.28. 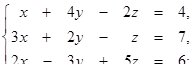
| 1.1.29. 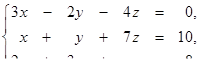
| 1.1.30. 
|
1.2. За координатами вершин піраміди  засобами векторної алгебри знайти:
засобами векторної алгебри знайти:
· довжину сторони  ,
,
· косинус кута між ребрами  і
і 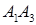 ,
,
· об’єм піраміди  ,
,
· роботу сили, що є рівнодіючою сил 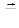 і
і  , під дією якої тіло переміщується прямолінійно з точки
, під дією якої тіло переміщується прямолінійно з точки  в точку
в точку  .
.
| 1.2.1. |  , ,  , , 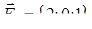
|
| 1.2.2. | 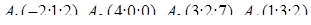 , , 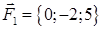 , , 
|
| 1.2.3. | 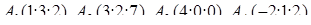 , , 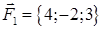 , , 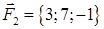
|
| 1.2.4. | 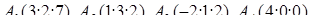 , , 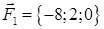 , , 
|
| 1.2.5. |  , , 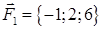 , , 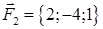
|
| 1.2.6. | 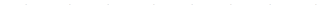 , , 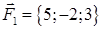 , , 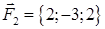
|
| 1.2.7. | 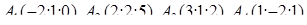 , , 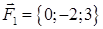 , , 
|
| 1.2.8. | 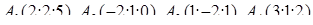 , ,  , , 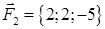
|
| 1.2.9. |  , , 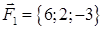 , , 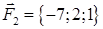
|
| 1.2.10. | 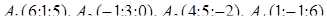 , , 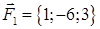 , , 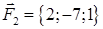
|
| 1.2.11. | 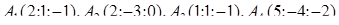 , , 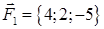 , , 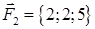
|
| 1.2.12. | 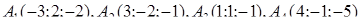 , , 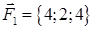 , , 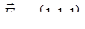
|
| 1.2.13. | 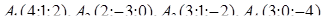 , , 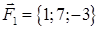 , , 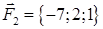
|
| 1.2.14. |  , ,  , , 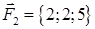
|
| 1.2.15. | 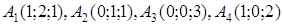 , ,  , , 
|
| 1.2.16. | 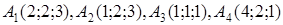 , ,  , , 
|
| 1.2.17. | 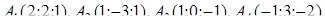 , , 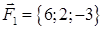 , , 
|
| 1.2.18 | 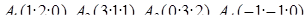 , , 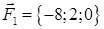 , , 
|
| 1.2.19. | 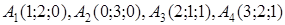 , ,  , , 
|
| 1.2.20. | 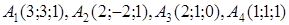 , ,  , , 
|
| 1.2.21. |  , ,  , , 
|
| 1.2.22 | 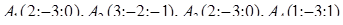 , , 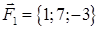 , , 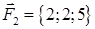
|
| 1.2.23 | 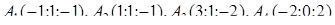 , , 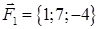 , , 
|
| 1.2.24 | 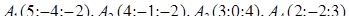 , , 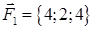 , , 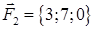
|
| 1.2.25 | 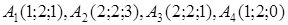 , , 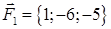 , , 
|
| 1.2.26 | 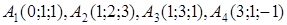 , ,  , , 
|
| 1.2.27 | 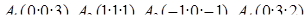 , , 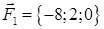 , , 
|
| 1.2.28 |  , , 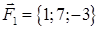 , , 
|
| 1.2.29 | 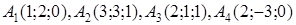 , , 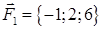 , , 
|
| 1.2.30 | 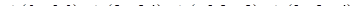 , , 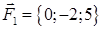 , , 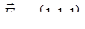
|
1.3. За координатами вершин трикутника 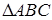 знайти:
знайти:
· рівняння лінії  ,
,
· рівняння висоти 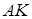 ,
,
· довжину висоти 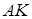 .
.
| 1.3.1. А(-5;2), В(2;-1), С(1;-2) | 1.3.2. А(1;1), В(-5;4), С(-2;5) |
| 1.3.3. А(0;3), В(2;4), С(-8;-1) | 1.3.4. А(-1;1), В(-7;4), С(-4;5) |
| 1.3.5. А(1;-3), В(3;-5), С(-5;7) | 1.3.6. А(1;-1), В(-5;2), С(-2;3) |
| 1.3.7. А(2;-1), В(4;2), С(5;1) | 1.3.8. А(-1;-1), В(-7;2), С(-4;3) |
| 1.3.9. А(9;6), В(-7;-6), С(0;18) | 1.3.10. А(1;0), В(7;3), С(4;4) |
| 1.3.11. А(1;1), В(7;4), С(4;5) | 1.3.12. А(7;1), В(-5;-4), С(-9;-1) |
| 1.3.13. А(-1;1), В(5;4), С(2;5) | 1.3.14. А(-2;1), В(-18;-11), С(-11;13) |
| 1.3.15. А(1;-1), В(7;2), С(4;5) | 1.3.16. А(10;-1), В(-2;-6), С(-6;-3) |
| 1.3.17. А(-1;-1), В(5;2), С(2;3) | 1.3.18. А(-12;6), В(12;-1), С(-6;23) |
| 1.3.19. А(0;1), В(6;4), С(3;5) | 1.3.20. А(8;0), В(-4;-5), С(-8;-2) |
| 1.3.21. А(6;2), В(30;-5), С(12;19) | 1.3.22. А(3;-5), В(4;1), С(5;-2) |
| 1.3.23. А(4;3), В(-12;-9), С(-5;15) | 1.3.24. А(-2;7), В(3;-3), С(2;5) |
| 1.3.25. А(-1;7), В(11;2), С(17;10) | 1.3.26. А(11;4), В(-1;-1), С(5;7) |
| 1.3.27. А(1;1), В(-15;11), С(-8;13) | 1.3.28. А(21;5), В(-3;-2), С(-7;11) |
| 1.3.29. А(-14;10), В(10;3), С(-8;27) | 1.3.30. А(20;5), В(-4;12), С(-8;9) |
1.4. Привести рівняння кола до канонічного виду, знайти центр кола та його радіус:
|
|
|
1.4.1. 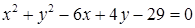
| 1.4.2. 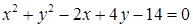
|
1.4.3. 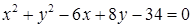
| 1.4.4. 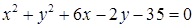
|
1.4.5. 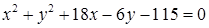
| 1.4.6. 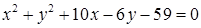
|
1.4.7. 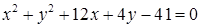
| 1.4.8. 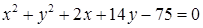
|
1.4.9. 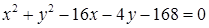
| 1.4.10. 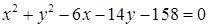
|
1.4.11. 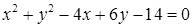
| 1.4.12. 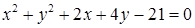
|
1.4.13. 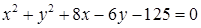
| 1.4.14. 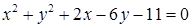
|
1.4.15. 
| 1.4.16. 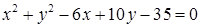
|
1.4.17. 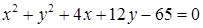
| 1.4.18. 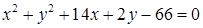
|
1.4.19. 
| 1.4.20. 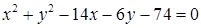
|
1.4.21. 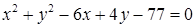
| 1.4.22. 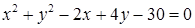
|
1.4.23. 
| 1.4.24. 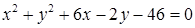
|
1.4.25. 
| 1.4.26. 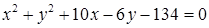
|
1.4.27. 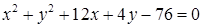
| 1.4.28. 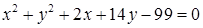
|
1.4.29. 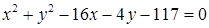
| 1.4.30. 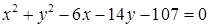
|
1.5. За координатами точок 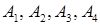 із завдання 1.2.х. знайти:
із завдання 1.2.х. знайти:
· рівняння площини  ,
,
· рівняння площини, що проходить через  паралельно
паралельно  ,
,
· довжину висоти  .
.
Модуль 2 . Вступ в математичний аналіз
|
|
|
2.1. Знайти границі:
| 2.1.1. | 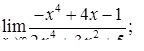
|  , ,
| 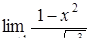 , ,
|
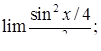
| 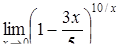 , ,
|  . .
| |
| 2.1.2. | 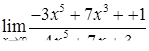 , ,
| 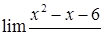 , ,
| 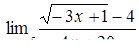 , ,
|
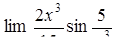 , ,
| 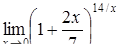 , ,
| 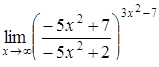 . .
| |
| 2.1.3. | 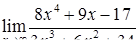 , ,
|  , ,
| 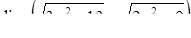 , ,
|
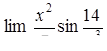 , ,
| 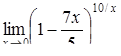 , ,
| 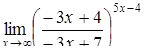 . .
| |
| 2.1.4. | 
|  , ,
| 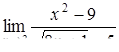 , ,
|
 , ,
| 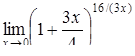
| 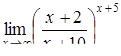 . .
| |
| 2.1.5. | 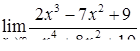 , ,
| 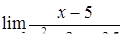 , ,
| 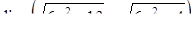 , ,
|
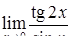 , ,
| 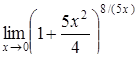 , ,
| 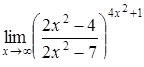 . .
| |
| 2.1.6. | 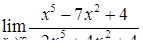 , ,
| 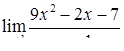 , ,
| 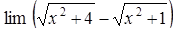 , ,
|
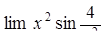 , ,
| 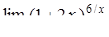 , ,
| 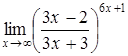 . .
| |
| 2.1.7. | 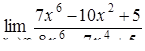 , ,
| 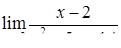 , ,
| 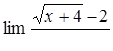 , ,
|
 , ,
|  , ,
| 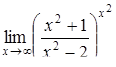 . .
| |
| 2.1.8. |  , ,
|  , ,
| 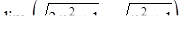 , ,
|
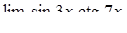 , ,
| 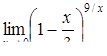 , ,
| 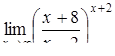 . .
| |
| 2.1.9. | 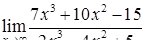 , ,
| 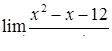 , ,
|  , ,
|
 , ,
| 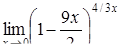 , ,
| 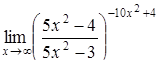 . .
|
| 2.1.10. | 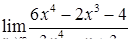 , ,
| 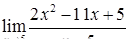 , ,
| 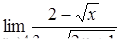 , ,
|
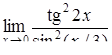 , ,
| 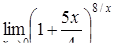 , ,
| 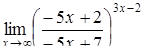 . .
| |
| 2.1.11. | 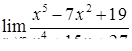 , ,
| 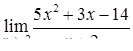 , ,
| 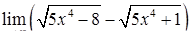 , ,
|
 , ,
| 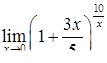 , ,
| 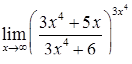 . .
| |
| 2.1.12. | 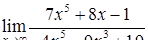 , ,
| 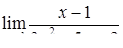 , ,
| 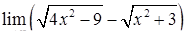 , ,
|
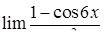 , ,
| 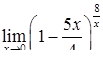 , ,
|  . .
| |
| 2.1.13. | 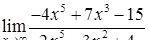 , ,
|  , ,
|  , ,
|
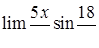 , ,
| 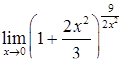 , ,
| 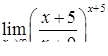 . .
| |
| 2.1.14. | 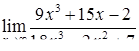 , ,
|  , ,
| 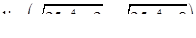 , ,
|
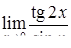 , ,
| 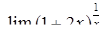 , ,
| 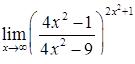 . .
| |
| 2.1.15. | 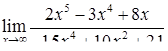 , ,
| 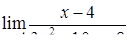 , ,
| 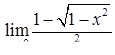 , ,
|
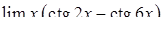 , ,
| 
| 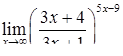 . .
| |
| 2.1.16. | 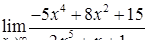 , ,
| 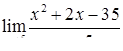 , ,
| 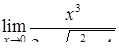 , ,
|
 , ,
| 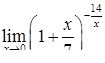 , ,
| 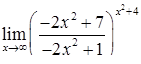 . .
| |
| 2.1.17. | 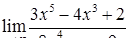 , ,
|  , ,
| 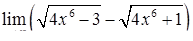 , ,
|
 , ,
| 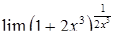 , ,
|  . .
| |
| 2.1.18. | 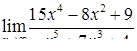 , ,
| 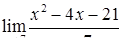 , ,
| 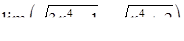 , ,
|
 , ,
| 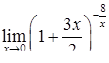 , ,
|  . .
| |
| 2.1.19. | 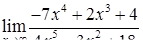 , ,
| 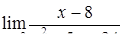 , ,
| 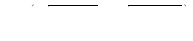 , ,
|
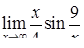 , ,
| 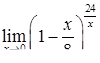 , ,
| 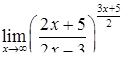 . .
| |
| 2.1.20. | 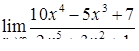 , ,
| 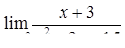 , ,
| 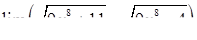 , ,
|
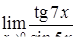 , ,
| 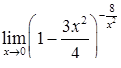 , ,
| 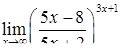 . .
| |
| 2.1.21. | 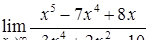 , ,
| 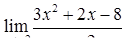 , ,
|  , ,
|
 , ,
| 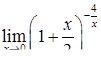 , ,
| 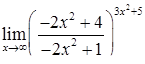 . .
| |
| 2.1.22. | 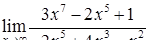 , ,
| 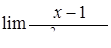 , ,
| 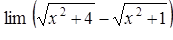 , ,
|
 , ,
|  , ,
| 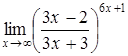 . .
| |
| 2.1.23. | 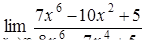 , ,
| 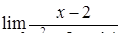 , ,
| 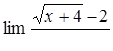 , ,
|
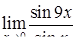 , ,
| 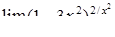 , ,
| 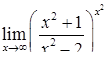 . .
| |
| 2.1.24. |  , ,
| 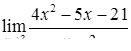 , ,
| 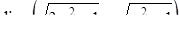 , ,
|
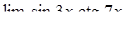 , ,
|  , ,
| 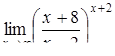 . .
| |
| 2.1.25. | 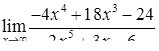 , ,
| 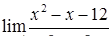 , ,
| 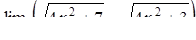 , ,
|
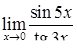 , ,
| 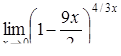 , ,
| 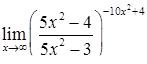 . .
| |
| 2.1.26. | 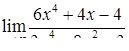 , ,
| 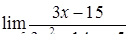 , ,
|  , ,
|
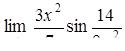 , ,
| 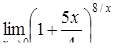 , ,
| 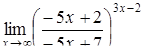 . .
| |
| 2.1.27. | 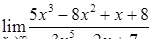
| 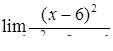 , ,
| 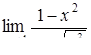 , ,
|
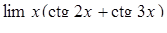 , ,
| 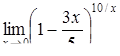 , ,
| 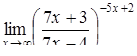 . .
| |
| 2.1.28. | 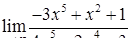 , ,
| 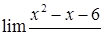 , ,
| 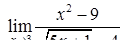 , ,
|
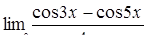 , ,
| 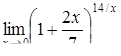 , ,
| 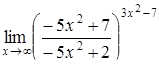 . .
| |
| 2.1.29. | 
| 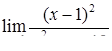 , ,
| 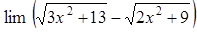 , ,
|
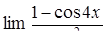 , ,
| 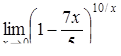 , ,
| 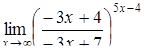 . .
| |
| 2.1.30. |  , ,
| 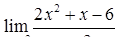 , ,
|  , ,
|
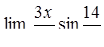 , ,
| 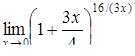 , ,
| 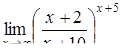 . .
|
2.2. Знайти похідну 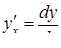 функцій:
функцій:
|
|
|
| 2.2.1. |  , ,
| 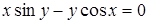 , ,
| 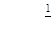 . .
|
| 2.2.2. |  , ,
| 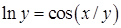 , ,
|  . .
|
| 2.2.3. |  , ,
| 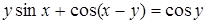 , ,
| 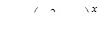 . .
|
| 2.2.4. |  , ,
| 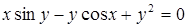 , ,
| 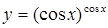 . .
|
| 2.2.5. | 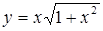 , ,
| 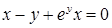 , ,
|  . .
|
| 2.2.6. |  , ,
|  , ,
| 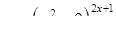 . .
|
| 2.2.7. | 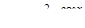 , ,
| 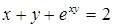 , ,
| 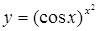 . .
|
| 2.2.8. |  , ,
|  , ,
|  . .
|
| 2.2.9. |  , ,
|  , ,
|  . .
|
| 2.2.10. | 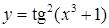 , ,
| 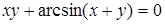 , ,
|  . .
|
| 2.2.11. | 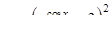 , ,
| 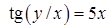 , ,
| 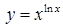 . .
|
| 2.2.12. |  , ,
| 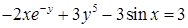 , ,
| 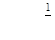 . .
|
| 2.2.13. |  , ,
|  , ,
| 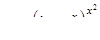 . .
|
| 2.2.14. |  , ,
| 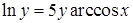 , ,
| 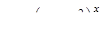 . .
|
| 2.2.15. | 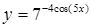 , ,
| 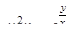
| 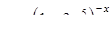 . .
|
| 2.2.16. | 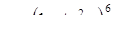 , ,
|  , ,
|  , ,
|
| 2.2.17. | 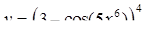 , ,
|  , ,
|  . .
|
| 2.2.18. | 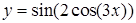 , ,
| 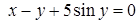 , ,
| 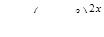 . .
|
| 2.2.19. |  , ,
| 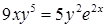 , ,
| 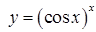 . .
|
| 2.2.20. | 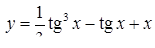 , ,
|  , ,
|  . .
|
| 2.2.21. |  , ,
| 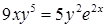 , ,
| 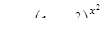 . .
|
| 2.2.22. |  , ,
| 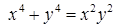 , ,
| 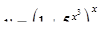 . .
|
| 2.2.23. | 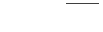 , ,
|  , ,
| 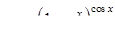 . .
|
| 2.2.24. | 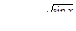 , ,
| 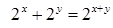 , ,
|  . .
|
| 2.2.25. | 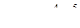 , ,
|  , ,
|  . .
|
| 2.2.26. | 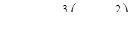 , ,
|  , ,
|  . .
|
| 2.2.27. | 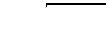 , ,
|  , ,
| 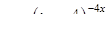 . .
|
| 2.2.28. | 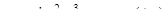 , ,
| 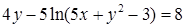 , ,
|  . .
|
| 2.2.29. | 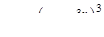 , ,
| 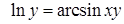 , ,
|  . .
|
| 2.2.30. | 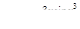 , ,
| 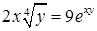 , ,
| 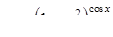 . .
|
2.3. Засобами диференціального числення дослідити функцію 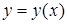 та побудувати її графік.
та побудувати її графік.
2.3.1. 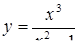
| 2.3.2. 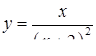
| 2.3.3. 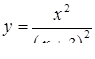
|
2.3.4. 
| 2.3.5. 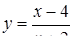
| 2.3.6. 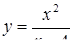
|
2.3.7. 
| 2.3.8. 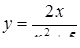
| 2.3.9. 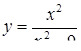
|
2.3.10. 
| 2.3.11. 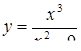
| 2.3.12. 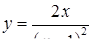
|
2.3.13. 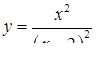
| 2.3.14. 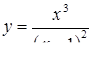
| 2.3.15. 
|
2.3.16. 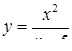
| 2.3.17. 
| 2.3.18. 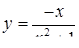
|
2.3.19. 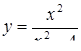
| 2.3.20. 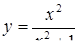
| 2.3.21. 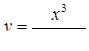
|
2.3.22. 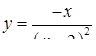
| 2.3.23. 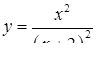
| 2.3.24. 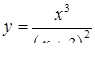
|
2.3.25. 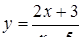
| 2.3.26. 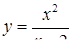
| 2.3.27. 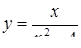
|
2.3.28. 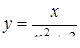
| 2.3.29. 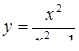
| 2.3.30. 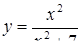
|
2.4. Тіло рухається прямолінійно за законом 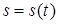 , де
, де 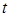 ‑ час (у секундах),
‑ час (у секундах), 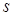 ‑ шлях (у метрах). Знайти в момент часу
‑ шлях (у метрах). Знайти в момент часу 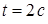 :
:
· миттєву швидкість,
· прискорення.
2.3.1. 
| 2.3.2. 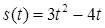
| 2.3.3. 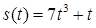
|
2.3.4. 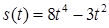
| 2.3.5. 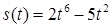
| 2.3.6. 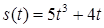
|
2.3.7. 
| 2.3.8. 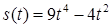
| 2.3.9. 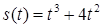
|
2.3.10. 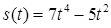
| 2.3.11. 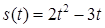
| 2.3.12. 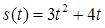
|
2.3.13. 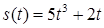
| 2.3.14. 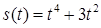
| 2.3.15. 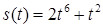
|
2.3.16. 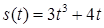
| 2.3.17. 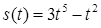
| 2.3.18. 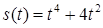
|
2.3.19. 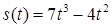
| 2.3.20. 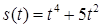
| 2.3.21. 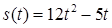
|
2.3.22. 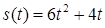
| 2.3.23. 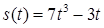
| 2.3.24. 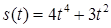
|
2.3.25. 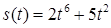
| 2.3.26. 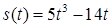
| 2.3.27. 
|
2.3.28. 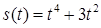
| 2.3.29. 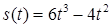
| 2.3.30. 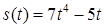
|
2.5. Для функції 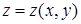 знайти:
знайти:
· похідну функції за напрямом вектора  в точці
в точці 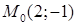 ,
,
· напрям найшвидшого зростання функції в точці 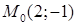 ,
,
· найбільше та найменше значення похідних за напрямом в точці 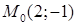 ,
,
· локальні екстремуми.
2.5.1. 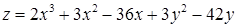
| 2.5.2. 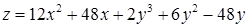
|
2.5.3. 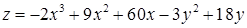
| 2.5.4. 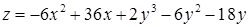
|
2.5.5. 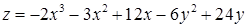
| 2.5.6. 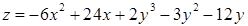
|
2.5.7. 
| 2.5.8. 
|
2.5.9. 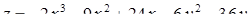
| 2.5.10. 
|
2.5.11. 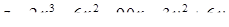
| 2.5.12. 
|
2.5.13. 
| 2.5.14. 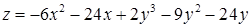
|
2.5.15. 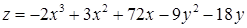
| 2.5.16. 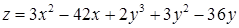
|
2.5.17. 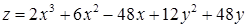
| 2.5.18. 
|
2.5.19. 
| 2.5.20. 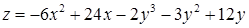
|
2.5.21. 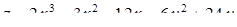
| 2.5.22. 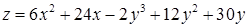
|
2.5.23. 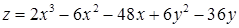
| 2.5.24. 
|
2.5.25. 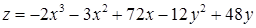
| 2.5.26. 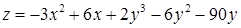
|
2.5.27. 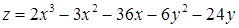
| 2.5.28. 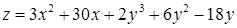
|
2.5.29. 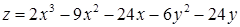
| 2.5.30. 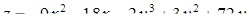
|
Модуль 3 . Невизначений і визначений інтеграли
3.1. Знайти невизначені та визначені інтеграли:
а) методом безпосереднього інтегрування,
б) методом заміни змінної (підстановки),
в) інтегруванням частинами,
г) від раціональної або ірраціональної функції шляхом виділення
повного квадрату у знаменнику,
д) способом перетворення добутків тригонометричних функцій у
суми.
| 3.1.1. | а) 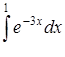 ,
б) ,
б)  ,
в) ,
в) 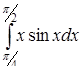 ,
г) ,
г) 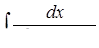 ,
д) ,
д)  . .
| 3.1.2. | а) 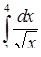 ,
б) ,
б) 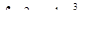 ,
в) ,
в) 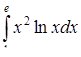 ,
г) ,
г) 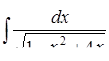 ,
д) ,
д) 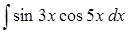 . .
|
| 3.1.3. | а) 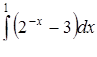 ,
б) ,
б) 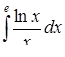 ,
в) ,
в)  ,
г) ,
г) 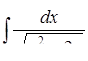 ,
д) ,
д) 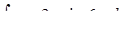 . .
| 3.1.4. | а) 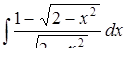 ,
б) ,
б) 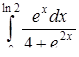 ,
в) ,
в) 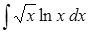 ,
г) ,
г) 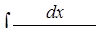 ,
д) ,
д)  . .
|
| 3.1.5. | а) 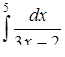 ,
б) ,
б) 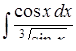 ,
в) ,
в)  ,
г) ,
г) 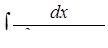 ,
д) ,
д)  . .
| 3.1.6. | а)  ,
б) ,
б) 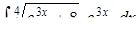 ,
в) ,
в) 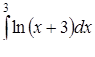 ,
г) ,
г) 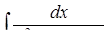 ,
д) ,
д) 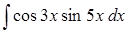 . .
|
| 3.1.7. | а) 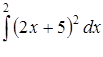 ,
б) ,
б) 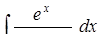 ,
в) ,
в) 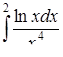 ,
г) ,
г) 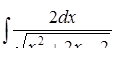 ,
д) ,
д) 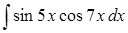 . .
| 3.1.8. | а)  ,
б) ,
б) 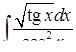 ,
в) ,
в) 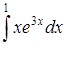 ,
г) ,
г) 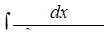 ,
д) ,
д)  . .
|
| 3.1.9. | а) 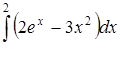 ,
б) ,
б) 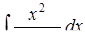 ,
в) ,
в) 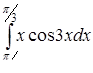 ,
г) ,
г) 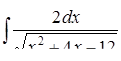 ,
д) ,
д)  . .
| 3.1.10. | а)  ,
б) ,
б) 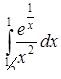 ,
в) ,
в) 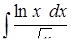 ,
г) ,
г) 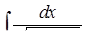 ,
д) ,
д)  . .
|
| 3.1.11. | а)  ,
б) ,
б) 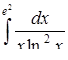 ,
в) ,
в) 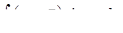 ,
г) ,
г) 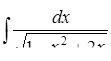 ,
д) ,
д) 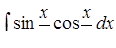 . .
| 3.1.12. | а) 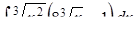 ,
б) ,
б) 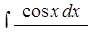 ,
в) ,
в) 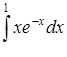 ,
г) ,
г) 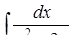 ,
д) ,
д)  . .
|
| 3.1.13. | а) 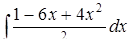 ,
б) ,
б) 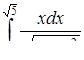 ,
в) ,
в) 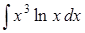 ,
г) ,
г)  ,
д) ,
д) 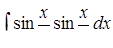 . .
| 3.1.14. | а) 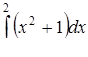 ,
б) ,
б) 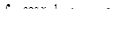 ,
в) ,
в) 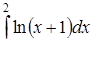 ,
г) ,
г) 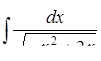 ,
д) ,
д) 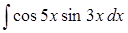 . .
|
| 3.1.15. | а)  ,
б) ,
б) 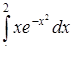 ,
в) ,
в)  ,
г) ,
г) 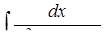 ,
д) ,
д) 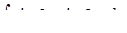 . .
| 3.1.16. | а) 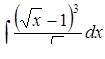 ,
б) ,
б)  ,
в) ,
в) 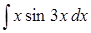 ,
г) ,
г) 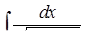 ,
д) ,
д)  . .
|
| 3.1.17. | а) 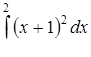 ,
б) ,
б) 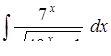 ,
в) ,
в) 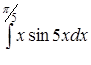 ,
г) ,
г) 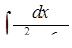 ,
д) ,
д) 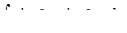 . .
| 3.1.18. | а) 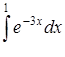 ,
б) ,
б) 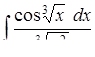 ,
в) ,
в) 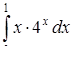 ,
г) ,
г) 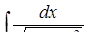 ,
д) ,
д)  . .
|
| 3.1.19. | а) 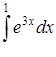 ,
б) ,
б)  ,
в) ,
в) 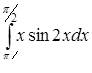 ,
г) ,
г) 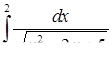 ,
д) ,
д)  . .
| 3.1.20. | а) 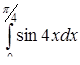 ,
б) ,
б) 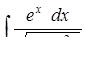 ,
в) ,
в) 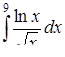 ,
г) ,
г) 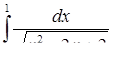 ,
д) ,
д) 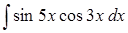 . .
|
| 3.1.21. | а) 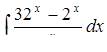 ,
б) ,
б) 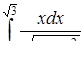 ,
в) ,
в) 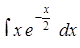 ,
г) ,
г) 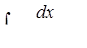 ,
д) ,
д)  . .
| 3.1.22. | а) 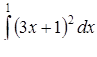 ,
б) ,
б) 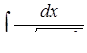 ,
в) ,
в) 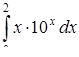 ,
г) ,
г) 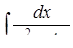 ,
д) ,
д) 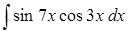 . .
|
| 3.1.23. | а)  ,
б) ,
б)  ,
в) ,
в) 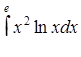 ,
г) ,
г) 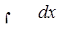 ,
д) ,
д)  . .
| 3.1.24. | а) 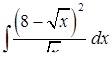 ,
б) ,
б) 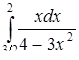 ,
в) ,
в) 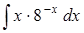 ,
г) ,
г) 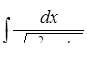 ,
д) ,
д) 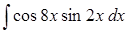 . .
|
| 3.1.25. | а) 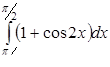 ,
б) ,
б) 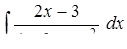 ,
в) ,
в) 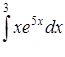 ,
г) ,
г) 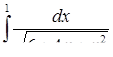 ,
д) ,
д) 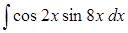 . .
| 3.1.26. | а) 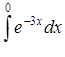 ,
б) ,
б)  ,
в) ,
в) 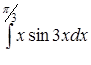 ,
г) ,
г) 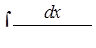 ,
д) ,
д) 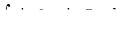 . .
|
| 3.1.27. | а) 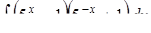 ,
б) ,
б) 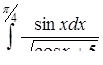 ,
в) ,
в) 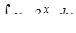 ,
г) ,
г) 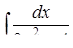 ,
д) ,
д) 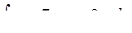 . .
| 3.1.28. | а)  ,
б) ,
б)  ,
в) ,
в) 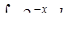 ,
г) ,
г) 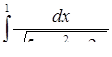 ,
д) ,
д)  . .
|
| 3.1.29. | а) 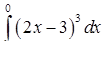 ,
б) ,
б) 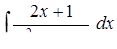 ,
в) ,
в) 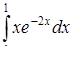 ,
г) ,
г)  ,
д) ,
д)  . .
| 3.1.30. | а) 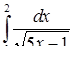 ,
б) ,
б) 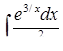 ,
в) ,
в) 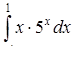 ,
г) ,
г) 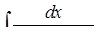 ,
д) ,
д)  . .
|
3.2. Дослідити на збіжність невласний інтеграл.
3.2.1. 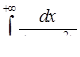
| 3.2.2. 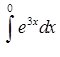
| 3.2.3. 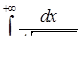
|
3.2.4. 
| 3.2.5. 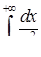
| 3.2.6. 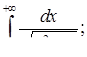
|
3.2.7. 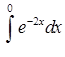
| 3.2.8. 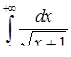
| 3.2.9. 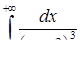
|
3.2.10. 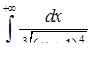
| 3.2.11. 
| 3.2.12. 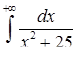
|
3.2.13. 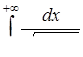
| 3.2.14. 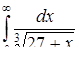
| 3.2.15. 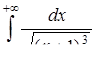
|
3.2.16. 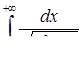
| 3.2.17. 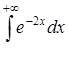
| 3.2.18. 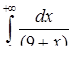
|
3.2.19. 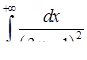
| 3.2.20. 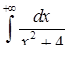
| 3.2.21. 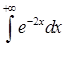
|
3.2.22. 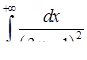
| 3.2.23. 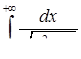
| 3.2.24. 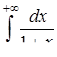
|
3.2.25. 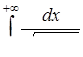
| 3.2.26. 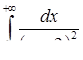
| 3.2.27. 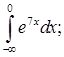
|
3.2.28. 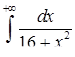
| 3.2.29. 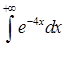
| 3.2.30. 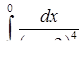
|
3.3. За допомогою інтегрального числення для обмеженої заданими лініями плоскої фігури 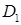 :
:
· обчислити площу,
· знайти координати центра ваги, якщо густина маси 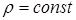 ,
,
· обчислити об’єм тіла, що утворюється при обертанні фігури 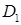 навколо вісі
навколо вісі 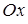 .
.
3.3.1. 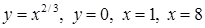
| 3.3.2. 
|
3.3.3. 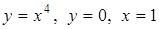
| 3.3.4. 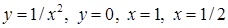
|
3.3.5. 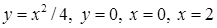
| 3.3.6. 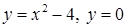
|
3.3.7. 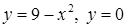
| 3.3.8. 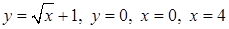
|
3.3.9. 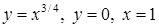
| 3.3.10. 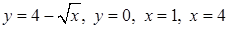
|
3.3.11. 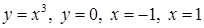
| 3.3.12. 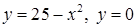
|
3.3.13. 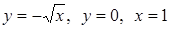
| 3.3.14. 
|
3.3.15. 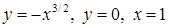
| 3.3.16. 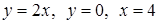
|
3.3.17. 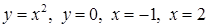
| 3.3.18. 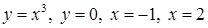
|
3.3.19. 
| 3.3.20. 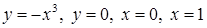
|
3.3.21. 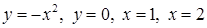
| 3.3.22. 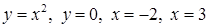
|
3.3.23. 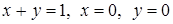
| 3.3.24. 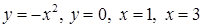
|
3.3.25. 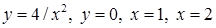
| 3.3.26. 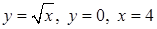
|
3.3.27. 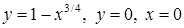
| 3.3.28. 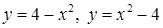
|
3.3.29. 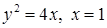
| 3.3.30. 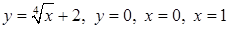
|
Дата добавления: 2018-09-22; просмотров: 281; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
