Розкриття невизначеностей, І і ІІ визначні границі
Обчислення границь базується на таких основних теоремах:
· Якщо існують 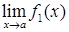 і
і 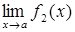 , то:
, то: 
 , (2.1.1)
, (2.1.1)
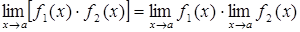 , (2.1.2)
, (2.1.2)

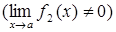 , (2.1.3)
, (2.1.3)
 . (2.1.4)
. (2.1.4)
· Перша визначна границя:
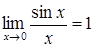 . (2.1.5)
. (2.1.5)
· Друга визначна границя:
 . (2.1.6)
. (2.1.6)
·  ;
; 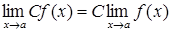 , (
, ( 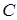 ‑ стала величина). (2.1.7)
‑ стала величина). (2.1.7)
· Для всіх неперервних функцій
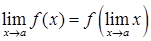 . (2.1.8)
. (2.1.8)
· Слід пам'ятати, що (для 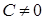 ):
): 

 , якщо
, якщо 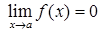 ;
; 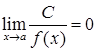 , якщо
, якщо  .
.
Щодо техніки обчислення границь, слід відзначити, що в найпростіших випадках знаходження границі зводиться до підстановки у вираз під знаком границі граничного значення аргументу. Але часто така підстановка призводить до невизначених виразів виду 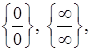
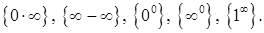 Знаходження границь у цих випадках називається розкриттям невизначеності.
Знаходження границь у цих випадках називається розкриттям невизначеності.
Наприлад, якщо невизначеність 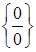 з’явиться, коли в чисельнику (знаменнику) є ірраціональний вираз, тоді треба позбутися ірраціональність у чисельнику (знаменнику) шляхом помноження на "спряжений" вираз.
з’явиться, коли в чисельнику (знаменнику) є ірраціональний вираз, тоді треба позбутися ірраціональність у чисельнику (знаменнику) шляхом помноження на "спряжений" вираз.
Невизначеність виду 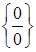 при наявності тригонометричних функцій розкривається за допомогою першої визначної границі та часто вимагає попередніх тотожних перетворень (наприклад, за допомогою формул:
при наявності тригонометричних функцій розкривається за допомогою першої визначної границі та часто вимагає попередніх тотожних перетворень (наприклад, за допомогою формул: 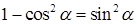 ,
,  ,
, 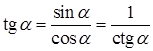 ,
, 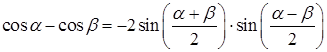 ).
).
Друга визначна границя розкриває невизначеність 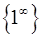 . Наслідками (2.1.6) є вирази:
. Наслідками (2.1.6) є вирази:
 ,
, 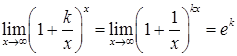 . (2.1.9)
. (2.1.9)
Приклад 2.1. 1. Знайти границі: 1)  , 2)
, 2) 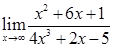 , 3)
, 3) 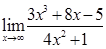 .
.
|
|
|
Розв’язання. 1) Маємо невизначеність 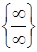 . Винесемо в чисельнику і знаменнику старший ступінь змінної і скоротимо:
. Винесемо в чисельнику і знаменнику старший ступінь змінної і скоротимо:
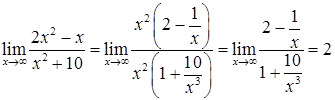 (тому, що
(тому, що 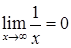 ,
,  ).
).
Аналогічно,
2) 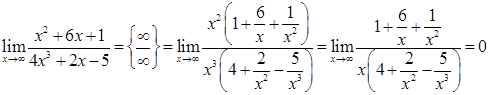 ;
;
3) 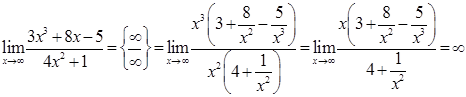 .
.
Приклад 2.1. 2 . Обчислити 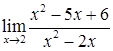 .
.
Розв’язання. В даному випадку користуватися формулою (2.1.3) не можна, тому що границя знаменника дорівнює нулеві. Безпосередня же підстановка у вираз під знаком границі граничного значення аргументу 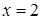 приводить до невизначеності
приводить до невизначеності  .
.
Розкладемо на множники чисельник і знаменник. (Зауважимо, що 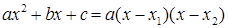 , якщо
, якщо  ‑ корені). Коренями квадратного рівняння
‑ корені). Коренями квадратного рівняння  є
є 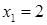 ,
,  , значить
, значить  .
.
Отже, за рахунок розкладання на множники і скорочення, позбавляємось невизначеності, після чого в результаті підстановки в отриманий вираз 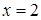 маємо
маємо
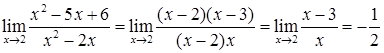 .
.
Приклад 2.1.3 . Обчислити 1) 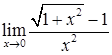 , 2)
, 2) 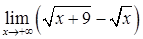 .
.
Розв’язання. 1) Підстановка у вираз (під знаком границі) 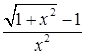 значення
значення 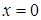 приводить до невизначеності
приводить до невизначеності 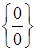 . Для її розкриття помножимо чисельник і знаменник на вираз, що "спряжений" з чисельником (користуючись формулою скороченного множення
. Для її розкриття помножимо чисельник і знаменник на вираз, що "спряжений" з чисельником (користуючись формулою скороченного множення  ). Після цього скоротимо на
). Після цього скоротимо на  і одержимо:
і одержимо:
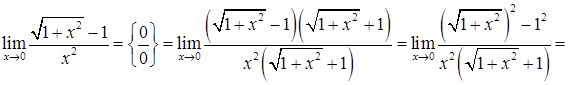
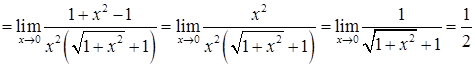 .
.
2) У випадку  маємо невизначеність
маємо невизначеність 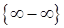 . Помноження і ділення виразу під знаком границі на "спряжений" з ним вираз
. Помноження і ділення виразу під знаком границі на "спряжений" з ним вираз 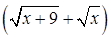 з урахуванням (2.1.7)) дає:
з урахуванням (2.1.7)) дає:
|
|
|
 .
.
Приклад 2.1.4 . Знайти границі: 1)  , 2)
, 2)  , 3)
, 3) 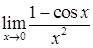 .
.
Розв’язання. Враховуючи, що 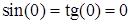 ,
,  , за допомогою формул тригонометрії, властивості (2.1.2) та першої визначної (2.1.5) маємо:
, за допомогою формул тригонометрії, властивості (2.1.2) та першої визначної (2.1.5) маємо:
1) 
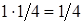 ,
,
2) 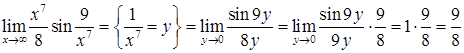 ,
,
3) 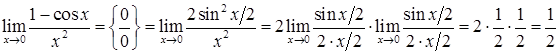 .
.
Приклад 2.1.5 . Знайти границі: 1) 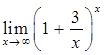 , 2)
, 2) 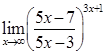 .
.
Розв’язання. Маємо невизначеність 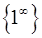 , яка розкривається за допомогою другої визначної границі (2.1.6).
, яка розкривається за допомогою другої визначної границі (2.1.6).
1) 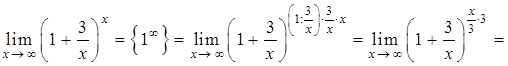
 (відповідь у данному випадку можна було отримати безпосередньо за (2.1.9)).
(відповідь у данному випадку можна було отримати безпосередньо за (2.1.9)).
2) 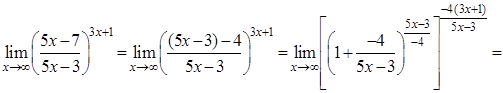
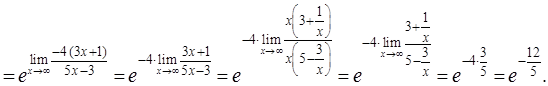
Зауважимо, що приклади 2.1.1 – 2.1.5 відповідають завданню 2.1 контрольної роботи.
Література: [1, с. 93 ‑ 125], [2, с. 101 ‑ 134], [3, с. 172 – 208, 247 ‑ 264], [7].
Дата добавления: 2018-09-22; просмотров: 278; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
