Визначники, матриці, розв’язання систем лінійних рівнянь
Методами оберненої матриці, Крамера, Гаус с а
Визначником(детермінантом) другого порядку називається число, яке обчислюється за формулою
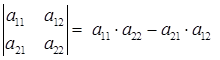. (1.1.1)
Приклад 1.1.1. Обчислити визначник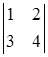 
.
Розв’язання. За формулою (1.1.1) маємо: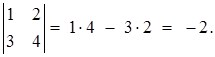 
Визначником третього порядку називається число, яке визначається формулою
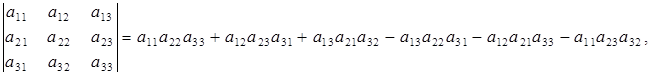(1.1.2)
і обчислення якого можна ілюструвати за допомогою наступної схеми:
«+» «‑»
Рис. 1.1.1 ‑ Правило трикутника
Таким чином, у суму (1.1.2) зі своїм знаком входять добутки елементів, розташованих на головній діагоналі (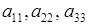 
) та на відповідних трикутниках (паралелі до головної діагоналі з’єднуються з протилежним кутом таблиці), а з протилежним знаком ‑ добутки елементів, розташованих на побічній діагоналі та на відповідних трикутниках (паралелі до побічної діагоналі з’єднуються з протилежним кутом).
Приклад 1.1.2. Обчислити визначник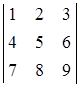 
.
Розв’язання. За формулою (1.1.2) маємо:
.
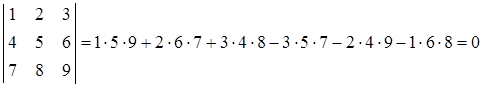Мінором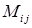 
елемента 
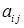називається визначник, який утворюється з даного викреслюванням i-го рядка і j-го стовпчика, на яких розташований елемент 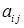. Алгебраїчним доповненням 
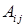елемента 
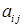називається мінор, помножений на 
. Отже, 
.
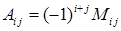Приклад 1.1.3. Знайти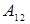 
для визначника з прикладу 1.1.2.
Розв’язання.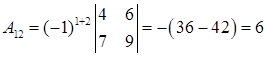 
.
Матрицею називається таблиця чисел. Матриця має розмірність (n´m), де n – кількість рядків, m – кількість стовпчиків. Якщо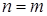 
, матриця називається квадратною.
|
|
|
На головній діагоналі квадратної матриці розташовані елементи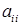 
, для яких номер рядка та стовпчика співпадають. Якщо всі елементи нижче (вище) головної діагоналі квадратної матриці дорівнюють нулю, то матриця називається трикутною.
Якщо визначник (позначення: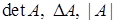 
) квадратної матриці 
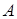не дорівнює нулю, то матриця називається невиродженою.
Транспонованою матрицею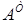 
називається матриця, у якої рядки записані замість стовпчиків (стовпчики ‑ замість рядків).
Сумою двох матриць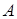 
і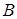 
однакової розмірності називається матриця 
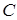, елементи якої дорівнюють сумі відповідних елементів матриць 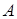і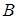 
.
Добутком матриці 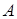на число k називається матриця, елементами якої є 
.
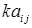Добутком матриці 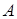розмірності (n´k)на матрицю 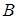розмірності (k´m) називається матриця 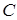розмірності (n´m), кожний елемент 
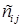якої дорівнює скалярному добутку (див. формулу (1.2.4)) -го вектора‑рядка матриці 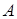на -й вектор‑стовпчик матриці .
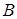Приклад 1.1.4.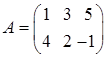 
, 
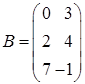. Знайти 
.
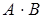Розв’язання. Матриця 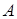розмірності 
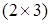, а матриця ‑ 
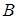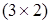, отже 
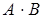буде мати розмірність 
(множити 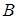на 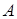не можна). 
.
|
|
|
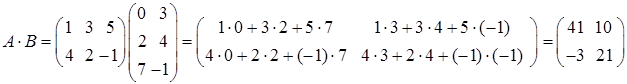Одиничною матрицею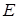 
називається матриця, елементи головної діагоналі якої дорівнюють одиниці, а всі інші ‑ нулю.
Оберненою матрицею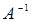 
до невиродженої матриці 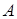називається матриця, для якої виконується рівність
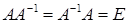. (1.1.3)
Матрицю 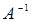(розмірності 3´3) можна знайти за формулою
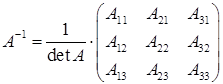. (1.1.4)
Розглянемо систему трьох лінійних рівнянь з трьома невідомими:
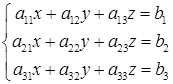. (1.1.5)
Позначимо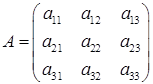 
‑ матриця системи, 
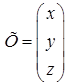‑ стовпчик невідомих, 
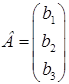‑ стовпчик вільних членів, тоді систему (1.1.5) можна записати в матричному виді:
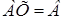. (1.1.6)
Якщо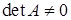 
, то розв’язок системи (1.1.6) має вигляд:
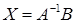, (1.1.7)
та може бути знайдений за методом оберненої матриці.
Якщо 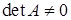, то за формулами Крамера розв’язком (1.1.5) є:
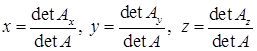, (1.1.8)
де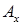 
( 
, 
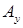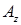) ‑ матриця, одержана із матриці 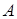заміною стовпця із коефіцієнтів при невідомому 
( 
, 
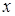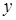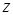) стовпчиком вільних членів.
Метод Гаусса розв’язання системи складається з двох кроків: спочатку система шляхом виключень невідомих приводиться еквівалентними перетвореннями до трикутного виду (тобто матриця отриманої системи є трикутною). Зазначимо, що
|
|
|
· множення (або ділення) обох частин будь якого рівняння системи на число, що не дорівнює нулю;
· додавання (або віднімання) рівнянь
є еквівалентними перетвореннями системи, тобто не змінюють її розв’язку. Зауважимо, що метод Гаусса є застосовним не лише для систем, матриця яких є квадратною.
Приклад 1.1. 1. Розв’язати систему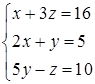 
методом оберненої матриці.
Розв’язання. Матриця системи (із коефіцієнтів при невідомих)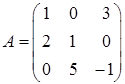 
, її визначник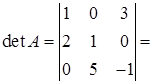 
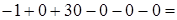
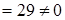. Значить, матриця 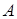має обернену.
Для побудови 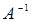запишемо спочатку алгебраїчні доповнення:
, 
, 
,
, 
, 
, 
, 
, 
.
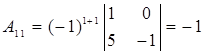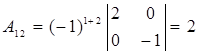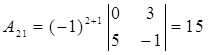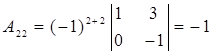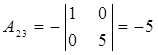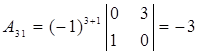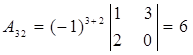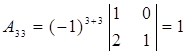Тоді за формулою (1.1.4) обернена матриця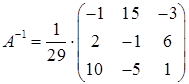 
.
Значить, згідно формули (1.1.7)
.
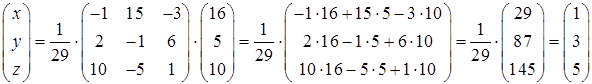Отже,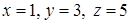 
.
Приклад 1.1. 2 . Розв’язати систему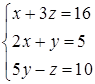 
методом Крамера.
Розв’язання. Матриця системи (із коефіцієнтів при невідомих) 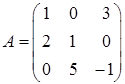, її визначник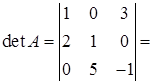 
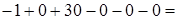
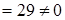. Значить, систему можна розв’язати за методом Крамера.
Допоміжні визначники:
, 
, 
.
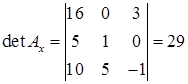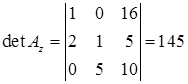Тоді за формулами Крамера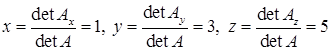 
.
Отже, .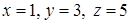
Приклад 1.1.3. Розв’язати систему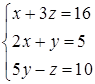 
методом Гаусса.
Розв’язання. Розв’яжемо систему методом Гаусса. Перше рівняння запишемо без змін. З усіх інших рівнянь виключимо невідому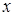 
. (Без змін можна записати будь-яке рівняння системи і обрати для виключення з усіх інших рівнянь будь-яку невідому, що входить в це рівняння з ненульовим коефіцієнтом). Якщо помножити перше рівняння на (-2) і додати до другого рівняння: 
, то після цього перетворення друге рівняння матиме вигляд: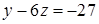 
. Третє рівняння вже не містить 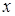. (Інакше ми б помножили перше та третє рівняння на такі числа, щоб додавання отриманих рівнянь призвело до зникнення 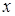). Отримали систему 
.
|
|
|
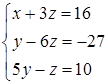Тепер перше та друге рівняння запишемо без змін, а з третього рівняння виключимо невідому 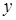. Для цього помножимо друге рівняння на (-5) і додамо до третього рівняння: 
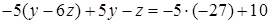. Отримаємо третє рівняння вже без невідомої : 
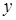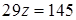. Таким чином, ми шляхом елементарних перетворень призвели систему до еквівалентного трикутного виду: 
.
З останнього рівняння, яке містить лише одну змінну, знаходимо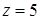 
, потім із передостаннього 
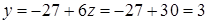. Підставляючи знайдені значення в перше рівняння, маємо 
.
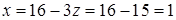Отже,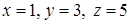 
.
Зауважимо, що приклади 1.1.1 ‑ 1.1.3 відповідають завданню 1.1 контрольної роботи.
Література: [1, с. 281 ‑ 294], [2, с. 383 ‑ 389], [3, с. 23 – 35, 64 ‑ 81], [5], [6].
Елементи векторної алгебри
Щоб знайти координативектора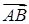 
, потрібно із координат його кінця відняти координати початку :
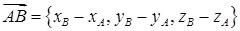. (1.2.1)
Довжина (модуль) вектора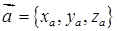 
дорівнює кореню квадратному із суми квадратів його координат:
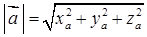. (1.2.2)
Ортом або одиничним вектором називається вектор, довжина якого дорівнює одиниці. Координатні орти:
.
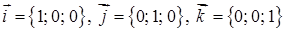При складанні (відніманні) векторів їхні координати складаються (віднімаються), а при множенні вектора на число його координати помножуються на це число.
Скалярним добутком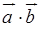 
векторів 
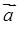і 
називається число, що дорівнює добутку їхніх довжин на косинус кута між ними:
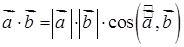. (1.2.3)
Якщо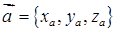 
, 
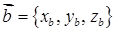тоді скалярний добуток
. (1.2.4)
Якщо матеріальна точка (тіло) під дією постійної за величиною і напрямом сили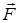 
переміщується уздовж вектора 
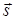, то робота сили обчислюється за формулою :
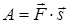. (1.2.5)
Векторний добуток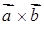 
– це вектор
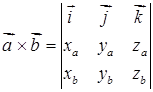. (1.2.6)
Якщо вектори 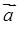і мають спільний початок, то модуль векторного добутку дорівнює площі паралелограма, побудованого на цих векторах (обо подвоєній площі прямокутника).
Мішаним добутком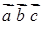 
трьох векторів 
, 
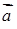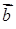і 
називається їх векторно-скалярний добуток:
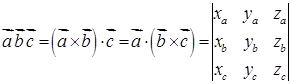. (1.2.7)
Якщо вектори 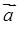, і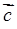 
мають спільний початок, то модуль мішаного добутку дорівнює об’ємові паралелепіпеда, побудованого на цих векторах (обо шести об’ємам піраміди).
У випадку
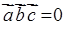, (1.2.8)
то вектори 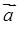, і 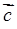є компланарними, тобто лежать в одній площині.
Вектори 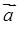, є колінеарними ( 
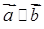), якщо
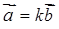, (1.2.9)
де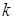 
‑ ненульове число.
Вектори 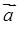, є ортогональними (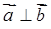 
), якщо
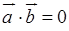. (1.2.10)
Приклад 1.2.1. За координатами вершин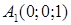 
, 
, 
, 
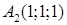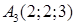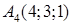піраміди 
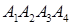знайти: а) довжину сторони 
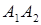, б) косинус кута між ребрами 
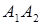і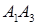 
, в) об’єм піраміди 
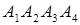, г) роботу рівнодіючої сил 
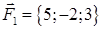і 
, під дією якої тіло переміщується прямолінійно з точки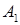 
в точку 
.
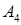Розв’язання. Знайдемо вектори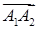 
, 
, 
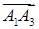за формулою (1.2.1): 
, 
, 
.
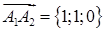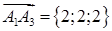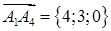а) Тоді за формулою (1.2.2) довжина сторони дорівнює 
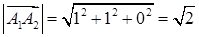(од.)
б) Згідно (1.2.3) та (1.2.4):
.
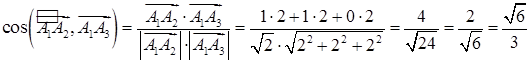в) Об’єм піраміди (шоста частина об’єма паралелепіпеда, побудованого на тих самих векторах) із застосуванням (1.2.7):
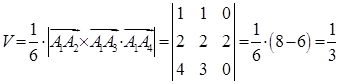(куб. од.),
г) Рівнодіюча сил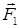 
і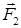 
‑ це сила 
, робота цієї сили згідно (1.2.5):
.
Зауважимо, що приклад 1.2.1 відповідає завданню 1.2 контрольної роботи.
Література: [1, с. 296 ‑ 315], [2, с. 402 ‑ 432], [3, с. 12 – 22, 35 ‑ 63], [5], [6].
Пряма на площині
Загальне рівняння прямої :
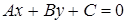. (1.3.1)
( 
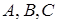‑ сталі числа, 
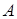і 
одночасно нулю не дорівнюють).
Рівняння прямої, яка має кутовий коефіцієнт k (тангенс кута між прямою і додатною піввіссюОх) і перетинає вісь Оу в точці, ордината якої дорівнює b, має вид:
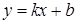. (1.3.2)
Рівняння прямої, яка проходить через точку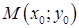 
в заданому напрямку :
. (1.3.3)
Рівняння прямої, що проходить через дві задані точки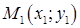 
і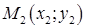 
, має вигляд:
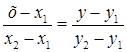. (1.3.4)
Рівняння прямої “у відрізках” на осях координат
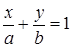. (1.3.5)
є зручним для побудови прямої на площині (пряма проходить через точки 
і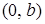 
, що розташовані на осях Ох і Оу відповідно).
Рівняння прямої, паралельної осі Ох, записується у вигляді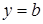 
, а прямої, паралельної осі Оу ‑ у виді 
.
Якщо є дві прямі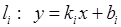 
(або 
), 
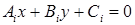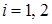, то
тангенс кута між прямими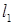 
і 
:
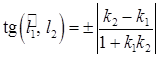. (1.3.6)
(знак плюс відповідає гострому куту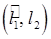 
, а знак мінус – тупому).
Умова паралельності прямих (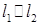 
):
, або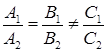 
. (1.3.7)
Умова перпендикулярності ( 
):
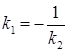, або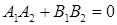 
. (1.3.8)
Відстань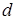 
точки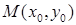 
до прямої 
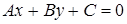знаходиться за формулою
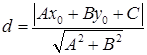. (1.3.9)
Приклад 1.3.1. За координатами вершин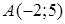 
, 
, 
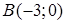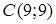трикутника 
знайти: а) рівняння лінії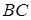 
, б) рівняння висоти 
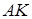, в) довжину висоти 
.
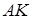Розв’язання. а) Знайдемо рівняння лінії, що проходить через точки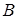 
і 
: 
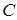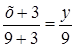, або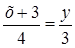 
, тобто 
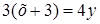. Таким чином, загальне рівняння : 
.
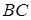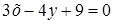б) Запишемо спочатку рівняння 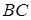з кутовим коефіцієнтом: 
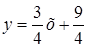. Таким чином, 
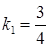‑ кутовий коефіцієнт прямої 
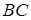. Пряма 
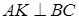, значить кутовий коефіцієнт прямої 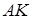згідно (1.3.8) дорівнює 
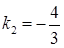. Користуючись рівнянням прямої (1.3.3), яка проходить через точку 
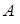в заданому напрямку, маємо рівняння : 
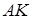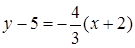, або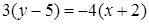 
, 
, 
.
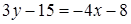в) Довжина висоти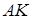 
‑ це відстань точки 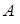до прямої 
. Значить, за формулою (1.3.9)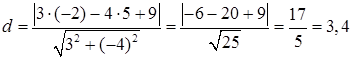 
(од.)
Зауважимо, що приклад 1.3.1 відповідає завданню 1.3 контрольної роботи.
Література: [1, с. 15 ‑ 45], [2, с. 33 ‑ 53], [3, с. 123 – 127], [5], [6].
Криві другого порядку
Канонічне рівняння кола з центром у точці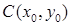 
і радіусом 
:
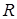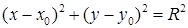. (1.4.1)
Канонічне рівняння еліпса:
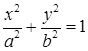. (1.4.2)
Канонічні рівняння гіперболи:
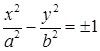. (1.4.3)
Канонічні рівняння параболи:
, 
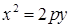. (1.4.4)
Приклад 1.4.1. Привести до канонічного виду рівняння кола 
, знайти центр та радіус.
Розв’язання. Поділимо рівняння на 25: 
. Згрупуємо члени, що містять лише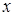 
і лише 
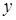, і доповнимо ці групи до повних квадратів: 
, 
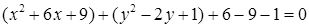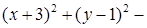
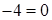. Отже маємо канонічне рівняння кола: 
.
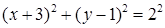Центром буде точка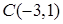 
, а радіус 
.
Зауважимо, що приклад 1.4.1 відповідає завданню 1.4 контрольної роботи.
Література: [1, с. 46 ‑ 57], [2, с. 54 ‑ 94], [3, с. 141 – 154], [5], [6].
Площина та пряма в просторі
Загальне рівняння площини:
. (1.5.1)
Вектор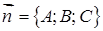 
є перпендикулярним до площини і називається нормальним.
Рівняння площини з нормальним вектором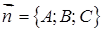 
, яка проходить через точку 
:
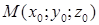. (1.5.2)
Рівняння площини у відрізках на осях:
. (1.5.3)
Рівняння площини, що проходить через три задані точки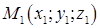 
, 
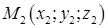і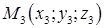 
, має вигляд:
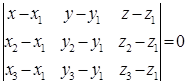. (1.5.4)
Відстань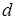 
точки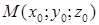 
до площини знаходиться за формулою
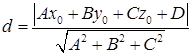. (1.5.5)
Канонічні рівняння прямої у просторі, що проходить через точку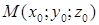 
паралельно до (напрямного) вектора 
:
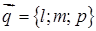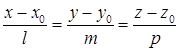. (1.5.6)
Рівняння прямої, яка проходить через дві задані точки:
. (1.5.7)
Загальні рівняння прямої (як лінії перетину двох площин):
(1.5.8)
Умова паралельності прямої і площини: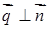 
, і згідно (1.2.10):
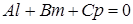. (1.5.9)
Умова перпендикулярності: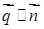 
, тобто згідно (1.2.9)
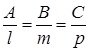. (1.5.10)
Приклад 1.5.1. За координатами точок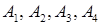 
із приклада 1.2.1 знайти: а) рівняння площини 
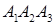, б) рівняння площини, що проходить через 
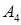паралельно 
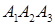, в) рівняння висоти 
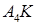, г) довжину висоти 
.
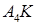Розв’язання. Координати точок ,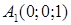 
, 
, 
.
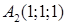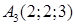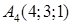а) Тоді рівняння площини 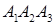згідно (1.5.4): 
, тобто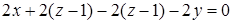 
, 
, 
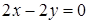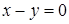. Значить, 
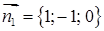‑ нормальний вектор площини 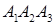, рівняння якої .
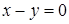б) Рівняння площини з нормальним вектором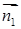 
, яка проходить через точку 
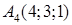згідно (1.5.2): 
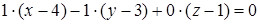, тобто 
, 
.
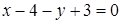в)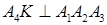 
, значить 
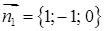‑ напрямний вектор прямої 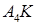. Таким чином, згідно (1.5.6) рівняння : 
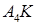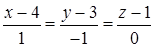(зауваження: 0 у знаменнику означає в данному випадку, що чисельник цього дробу дорівнює 0). Отже загальні рівняння (виду (1.5.8)) висоти : 
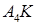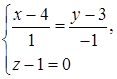тобто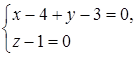 
г) Довжина висоти 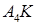‑ це відстань точки 
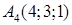до площини 
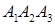. Значить, згідно (1.5.5) 
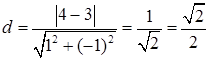(од.)
Зауважимо, що приклад 1.5.1 (а, б, г) відповідає завданню 1.5 контрольної роботи.
Література: [1, с. 316 ‑ 332], [2, с. 441 ‑ 471], [3, с. 110 – 140, 158 ‑171], [5], [6].
МОДУЛЬ 2
ВСТУП В МАТЕМАТИЧНИЙ АНАЛ ІЗ
Дата добавления: 2018-09-22; просмотров: 694; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!