Итерационные методы решения линейных алгебраических уравнений: метод Зейделя.
СЛАУ-система m линейных алгебраических уравнений с n неизвестными вида:
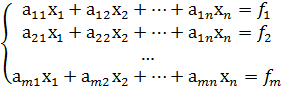(1)
m-количество уравнений, n-количество неизвестных, x1…xn-неизвестные, которые надо найти, a11…amn-коэффициенты системы, fm-свободные члены.
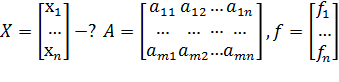СЛАУ (1) в матричном виде Аx=f
Итерационные методы устанавливают процедуру многократного уточнения определенного начального приближения к решению. Верхним индексом в скобках обозначается номер итерации(совокупность повторяющихся действий).
Идея метода Зейделя при нахождении i-й компоненты (k+1)-го приближения сразу используються уже найденные компоненты (k+1)-го приближения с меньшими номерами 1,2,…,i-1.Применим для n*n систем.
Рассмотрим стационарную схему
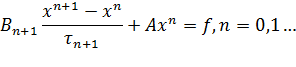
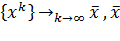- точное решение
А=А1+D+А2
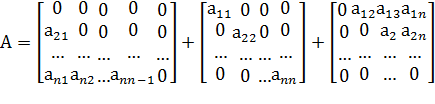Bn+1=D+A1 , τn+1=1, (D+A1)(xn+1-xn)+Axn=f
…
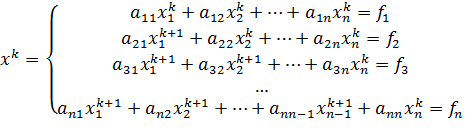
Теорема 1 (достаточное условие сходимости)
1. А=АТ (матрицы симметричны)
2.А>0 (Ах,х)>0, любого х≠0
Если 1,2 выполняются тогда метод Зейделя сходиться. 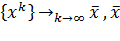- точное решение
Замечание: Условие 1 и 2 достаточны, но не является необходимым.
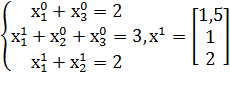
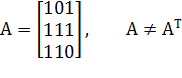Достаточное условие не выполняется процесс сходимости открыт
Пример
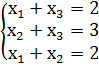
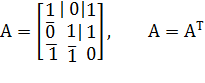Главные миноры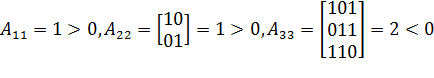 
Матрица А не является положительной.
1. Преобразовать систему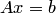 
к виду 
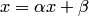одним из описанных способов.
2. Задать начальное приближение решения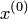 
произвольно или положить 
, а также малое положительное число 
(точность). Положить 
.
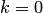3. Произвести расчеты по формуле (10.15) или (10.16) и найти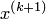 
.
4. Если выполнено условие окончания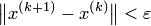 
, процесс завершить и в качестве приближенного решения задачи принять 
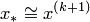. Иначе положить 
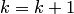и перейти к пункту 3.
|
|
|
16 Интерполяция многочленами: метод Лагранжа
Интерполяция – определение промежуточных значений функции по известному дискретному набору значений функции.
| xi | x0 | x1 | … | xn |
| fi(x) | f0 | f1 | … | fn |
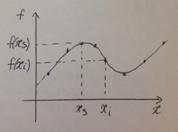
f(xs), xs≠xi, i=0,1…n
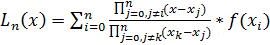-Интерполяционная формула Лагранжа
,
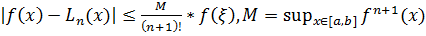М- точная верхняя грань
Теорема
Если f(x)-многочлен n-степени, то f(x)=Ln(x)
Разностные схемы для уравнения теплопроводности.
Рассмотрим смешанную краевую задачу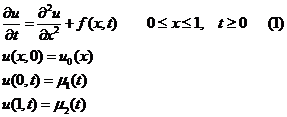 
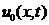-начальное распределение температуры, 
, 
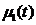-распределение температуры на концах рассматриваемого отрезка в любой момент времени.
Введем равномерную сетку ωn и ωτ: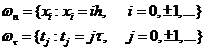 
.
h, τ – шаги по направлению x, t. Узел сетки имеет координаты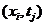 
. Декартово произведение: 
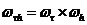. Слоем называется множество узлов из 
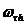при фиксированном t. Существуют и основные схемы решения уравнения теплопроводности.
1) Явная схема. ДУ (1) заменяется сеточнымна 4-х точечном шаблоне вида: тогда уравнение (1) примет вид: 
Начальные и граничные условия примут вид:
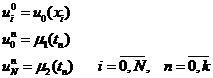
Схема связывает 2 слоя и называется двухслойной.
2)Неявная схема
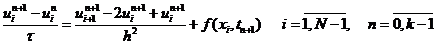
Начальные и граничные условия примут вид:
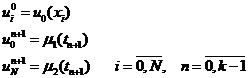
3)Трехслойная схема
|
|
|
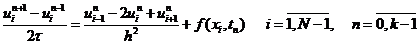
Начальные и граничные условия примут вид:
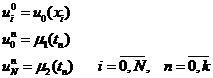
4)Симметричная или шеститочечная
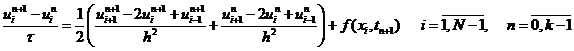
Начальные и граничные условия примут вид:
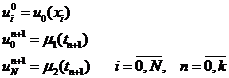
Дата добавления: 2018-06-27; просмотров: 269; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!