Собственные вектора и собственные значения матрицы.
Пусть дана матрица А
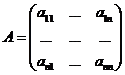
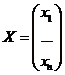
Собственным вектором матрицы А называется ненулевой вектор, для которого выполняется равенство АХ=λХ, а число λ называется собственным значением.
Для нахождения λ составляют характеристическое уравнение 
АХ=λХ

Получили систему линейных однородных уравнений. СЛОУ будет иметь ненулевое решение, если определитель системы равен нулю, т.е. 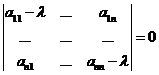
Алгоритм решения линейного неоднородного дифференциального уравнения первого порядка. Задача Коши.
Линейным дифференциальным уравнением 1-го порядка называется уравнение  потому что у и у’ входят в него линейно. Вместе с (1) рассматривается эквивалентная запись
потому что у и у’ входят в него линейно. Вместе с (1) рассматривается эквивалентная запись 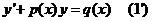
Если  , т.е. имеем
, т.е. имеем 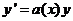 или
или 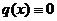 , т.е. имеем
, т.е. имеем 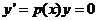 , то уравнение называется линейным однородным уравнением (ЛОДУ)
, то уравнение называется линейным однородным уравнением (ЛОДУ)
Если 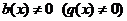 , то уравнение называется линейным неоднородным уравнением (ЛНДУ).
, то уравнение называется линейным неоднородным уравнением (ЛНДУ).
Для того, чтобы проинтегрировать ЛНДУ 1-го порядка, необходимо проинтегрировать соответствующее ему ЛОДУ 1-го порядка (т.е. решив промежуточную задачу, записав ноль в правой части), а затем применить метод Лагранжа.
1. Интегрирование ЛОДУ
Всякое ЛОДУ 1-го порядка интегрируется разделением переменных: 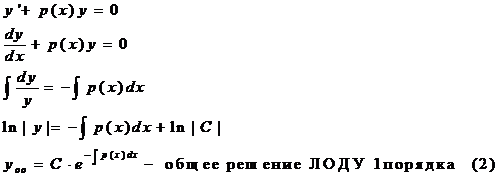
2. Метод Лагранжа (метод вариации постоянной)
В формуле (2) считать, что С является неизвестной функцией. Варьируем постоянную 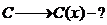 Найдем такую функцию С(х), чтобы формула (2) являлась решением ЛНДУ (1)
Найдем такую функцию С(х), чтобы формула (2) являлась решением ЛНДУ (1)
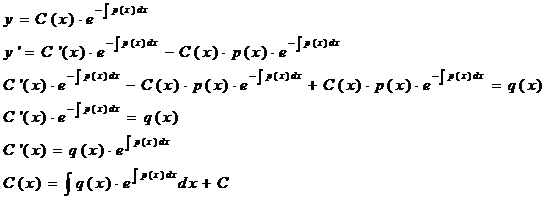
Подставляем
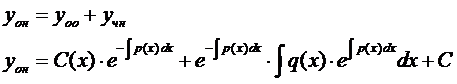
Закон является всеобщим и действует для всех ЛНДУ любого порядка
|
|
|
Задача Коши.Для того, чтобы из бесконечного числа решений выделить одно, необходимо дополнительное условие. Для ДУ 1-го порядка в нормальной форме:  . Таким дополнительным условием является условие Коши y(x0)=y0 – условие Коши. А такая задача называется задачей Коши: y'=f(x,y), y(x0)=y0, где x0, y0 – любые числа, начальные условия функции.
. Таким дополнительным условием является условие Коши y(x0)=y0 – условие Коши. А такая задача называется задачей Коши: y'=f(x,y), y(x0)=y0, где x0, y0 – любые числа, начальные условия функции.
Алгоритм решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами. Задача Коши.
Пусть дано ДУ: 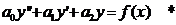 . С постоянными вещественными коэффициентами
. С постоянными вещественными коэффициентами  . Для каждого такого уравнения можно записать соответствующее однородное уравнение:
. Для каждого такого уравнения можно записать соответствующее однородное уравнение: 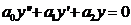
Теорема. Общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения.  .
.
1) Найдем 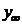
Рассмотрим ду: 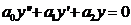 , где
, где  - вещественные постоянные. Составляем характеристическое уравнение
- вещественные постоянные. Составляем характеристическое уравнение  . Пусть λ1,λ2 корни уравнения, причем среди них могут быть и кратные.
. Пусть λ1,λ2 корни уравнения, причем среди них могут быть и кратные.
Возможны следующие случаи:
а) λ1,λ2 - вещественные и различные
Тогда ФСР уравнения (1) имеет вид  и общим решением однородного уравнения будет
и общим решением однородного уравнения будет  .
.
б) λ1,λ2 - вещественные и кратные. 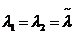 .
.
ФСР  , общее решение
, общее решение  .
.
в) λ1,λ2 – комплексные. 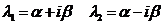 . ФСР
. ФСР  .
.
|
|
|
2) Найдем 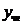
а) метод подбора.
Общий вид правой части f(x) уравнения (*), при котором возможно применить метод подбора, следующий: 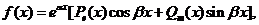 где
где 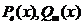 - многочлены степени e и m соответственно. В этом случае частное решение уравнения (*) ищется в виде
- многочлены степени e и m соответственно. В этом случае частное решение уравнения (*) ищется в виде 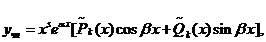 где
где  многочлены от х к-ой степени общего вида с неопределенными коэффициентами, а S – кратность корня характеристического уравнения.
многочлены от х к-ой степени общего вида с неопределенными коэффициентами, а S – кратность корня характеристического уравнения.
б) принцип суперпозиции
При нахождении частных решений ЛНДУ удобно пользоваться принципом суперпозиции.
Теорема. Если yk(x) ест решение уравнения 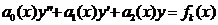 ,k=1,2.
,k=1,2.
То функция  является решением уравнения
является решением уравнения 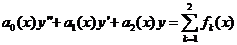 .
.
в) задача Коши.
Как известно з.К. для ЛНУ 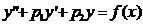 , состоит: в нахождении решения этого уравнения, удовлетворяющего начальным условиям:
, состоит: в нахождении решения этого уравнения, удовлетворяющего начальным условиям: 
Дата добавления: 2018-06-27; просмотров: 314; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
