Понятие определённого интеграла
Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где a не= b) называется приращение какой-нибудь её первообразной на этом отрезке. При этом употребляется запись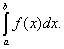 
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.
Таким образом, если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,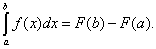 
(38) При a = b по определению принимается 
Равенство (38) называется формулой Ньютона-Лейбница. Разность F(b) – F(a) кратко записывают так: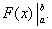 
Поэтому формулу Ньютона-Лейбница будем записывать и так: 
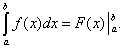(39)
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F(x) и Ф(х) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х) = F(x) + C. Поэтому 
Тем самым установлено, что на отрезке [a, b] приращения всех первообразных функции f(x) совпадают.
Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница: в первообразную функцию подставляется значение верхнего предела b, далее - значение нижнего предела a и вычисляется разностьF(b) - F(a). Полученное число и будет определённым интегралом..
|
|
|
Пример 1.Вычислить определённый интеграл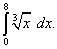 
Решение. Сначала найдём неопределённый интеграл: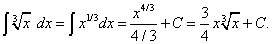 
Применяя формулу Ньютона-Лейбница к первообразной 
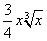(при С = 0), получим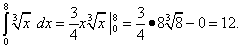 
Свойства определённого интеграла
1.Определённый интеграл с одинаковыми пределами интегрирования равен нулю, т.е.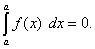 
Это свойство содержится в самом определении определённого интеграла. Однако его можно получить и по формуле Ньютона-Лейбница: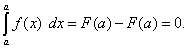 
2.Величина определённого интеграла не зависит от обозначения переменной интегрирования, т.е. 
3.Постоянный множитель можно выносить за знак определённого интеграла, т.е.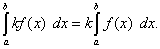 
4.Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций, т.е.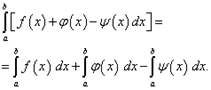 
5.Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям, т.е. если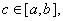 
то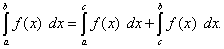 
6.При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е. 
7(теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке 
внутри его, т.е.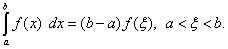 
|
|
|
8.Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если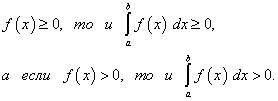 
9.Если верхний предел интегрирования больше нижнего и функции f(x) и φ(x) непрерывны, то неравенство f(x) >= φ(x) можно почленно интегрировать, т.е.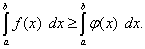 
ПримерВычисления определённый интеграла заменой переменны
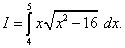
Решение. Произведём замену переменной, полагая
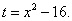
Тогда dt = 2x dx, откуда x dx= (1/2) dt, и подынтегральное выражение преобразуется так:
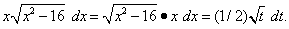
Найдём новые пределы интегрирования. Подстановка значений x = 4и x = 5в уравнение
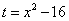
Даёт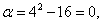 
а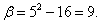 
Используя теперь формулу , получим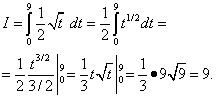 
После замены переменной мы не возвращались к старой переменной, а применили формулу Ньютона-Лейбница к полученной первообразной.
Дата добавления: 2018-06-27; просмотров: 350; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!