Интегральная функция распределения двумерной случайной величины.
Свойства интегральной функции распределения:
1. 
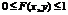
2. 
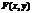—неубывающая функция по каждому аргументу
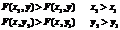
3.Имеют место следующие отношения:
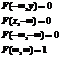
4.Если одна составляющая равна 
, то интегральная функция становится функцией другой составляющей:
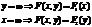
Вероятность попадания случайной точки в полуполосу
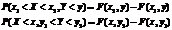
Вероятность попадания случайной точки в прямоугольник
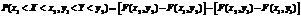
Дифференциальная функция непрерывной двумерной случайной величины
Нахождение интегральной функции по заданной дифференциальной
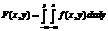
Вероятность попадания случайной точки в произвольную область
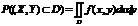
Свойства дифференциальной функции двумерной случайной величины
1. 
2. 
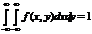
Отыскание дифференциальных функций составляющих двумерной случайной величины.
Условные законы распределения составляющих системы дискретных случайных величин.
Рассмотрим дискретную двумерную случайную величину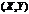 
, пусть возможные значения составляющих таковы:
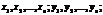
Предположим, что в результате испытания случайная величина Y приняла значение 
, тогда X может принять одно из своих возможных значений. Обозначим условную вероятность того, что X примет значение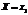 
через 
Условным распределением случайной величины X при условии, что Y приняла значение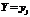 
называют совокупность условных вероятностей
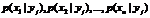
Зная закон распределения двумерной дискретной случайной величины можно вычислить условные законы распределения составляющих:
|
|
|
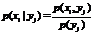
Условные законы распределения составляющих системы непрерывных случайных величин
Условной дифференциальной функцией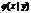 
составляющей X при условии, что 
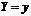, называют отношение дифференциальной функции системы к дифференциальной функции составляющей Y.
Условное математическое ожидание
Условным математическим ожиданием случайной величины Y при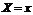 
называют сумму произведений возможных значений Y на их условные вероятности.
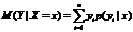
Для непрерывных величин:
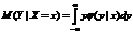
Зависимые и независимые случайные величины
Теорема.Для того чтобы случайные величины X и Y были независимы, необходимо и достаточно, чтобы интегральная функция системы 
была равна произведению интегральных функций случайных величин X и Y.
Следствие. Для того чтобы случайные величины X и Y были независимы, необходимо и достаточно, чтобы дифференциальная функция системы была равна произведению дифференциальных функций случайных величин X и Y.
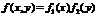
Числовые характеристики системы двух случайных величин.
Корреляционным моментом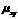 
случайных величин X и Y называют математическое ожидание произведения их отклонений.
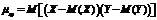
Для дискретных величин
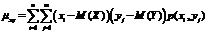
Для непрерывных величин
|
|
|
Теорема.Корреляционный момент двух независимых случайных величин равен 0
Коэффициентом корреляции независимых случайных величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин.
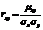
Дата добавления: 2018-05-13; просмотров: 502; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!