Математическое ожидание дискретной случайной величины.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.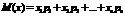

Вероятностный смысл математического ожидания.

Пусть произведено n испытаний, в которых случайная величина X приняла 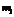раз значение 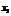, 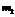раз значение 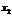,…, 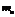раз значение 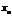, причем .

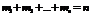Найдем среднее арифметическое 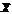всех значений, принятых случайной величиной.

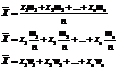
Математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.

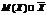
Свойства математического ожидания

1.

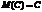
2.

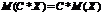
3.

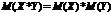
4.

Теорема.Математическое ожидание M(X) числа появлений события A в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании.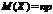

Дисперсия дискретной случайной величины.

Отклонением называют разность между случайной величиной и ее математическим ожиданием. Отклонение имеет следующий закон распределения:

Теорема. Математическое ожидание отклонения равно нулю.

Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения дискретной случайной величины от ее математического ожидания. Дисперсия нужна для того, чтобы оценить рассеяние дискретной случайной величины вокруг ее математического ожидания.

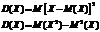
Свойства дисперсии

1.

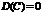
2.

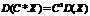
3.

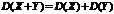
4.

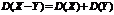
Теорема.Дисперсия числа появлений события A в n независимых испытаниях, в каждом из которых вероятность события A постоянна, равна произведению числа испытаний на вероятности появления и непоявления A в одном испытании.

Среднее квадратическое отклонение

Средним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии:

Теорема. Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин.

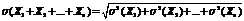
Одинаково распределенные независимые случайные величины.

Рассмотрим n взаимно независимых случайных величин 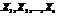, которые имеют одинаковые распределения, а следовательно и одинаковые характеристики.

Обозначим среднее арифметическое рассматриваемых случайных величин через

Математическое ожидание среднего арифметического n одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию a каждой из величин:

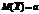
Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в n раз меньше дисперсии каждой из величин:

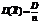
Среднее квадратическое среднего арифметического n одинаково распределенных взаимно независимых случайных величин в  раз меньше среднего квадратического каждой из величин:

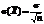
Моменты распределения

Начальным моментом порядка k случайной величины X называют математическое ожидание величины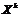

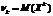
Центральным моментом порядка k случайной величины X называют математическое ожидание величины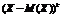

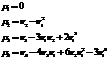
Неравенство Чебышева. Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа 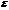 не меньше чем :

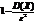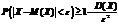
Теорема Чебышева. Если 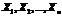попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают некоторого постоянного числа C), то, как бы мало не было число 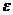, вероятность неравенства

Будет как угодно близка к единице, если число случайных величин достаточно велико.

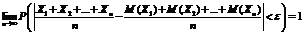
Если 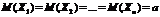, то

 

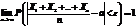
Теорема Бернулли.Если в каждом из n независимых испытаний вероятность p появления события A постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности p по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико:

---

Дата добавления: 2018-05-13; просмотров: 324; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!