Формула для вычисления вер-ти того, что случайная величина кот. подлежит норм. закону распред., принимает значения из интервала (a, b)
Вероятность попадания случайной величины Х, распределенной по нормальному закону, в интервал 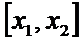 , равна
, равна 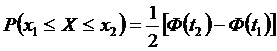 ,
,
Где  ,
, 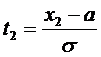 ; ( Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле:
; ( Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле: 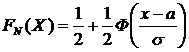 ).
).
□ Учитывая, что вероятность  есть приращение функции распределения на отрезке
есть приращение функции распределения на отрезке 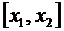 и учитывая формулу
и учитывая формулу 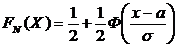 получим:
получим:
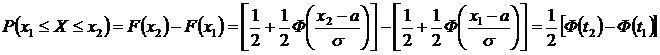 .
.
Сформулируйте првило трех сигм.
При рассм нормального закона распределения выделяется важный частный случай, известный как правило трех сигм. Запишем в-ть того что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:
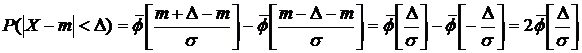
Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа: 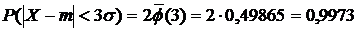
Т.е. в-ть того что случайная величинаотклонится от своего мат\ожидания на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю. Это правило называется правилом трех сигм.На практике считается, что если для какой – либо сл\величины выполняется правило трех сигм, то эта сл\величина имеет нормальное распределение.
СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
Определение понятия системы случайных величин.
Очень часто результат испытания характеризуется не одной Случ.Велич. а некоторой системой случайных величин 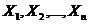 , которую называют также многомерной (n-мерной) случайной величиной или случайным вектором Х = (
, которую называют также многомерной (n-мерной) случайной величиной или случайным вектором Х = ( 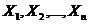 ). Приведем примеры многомерных случайных величин.
). Приведем примеры многомерных случайных величин.
|
|
|
1.Успеваемость выпускника вуза характеризуется системой n случайных величин 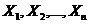 - оценками по различным дисциплинам, проставленными в приложении к диплому.
- оценками по различным дисциплинам, проставленными в приложении к диплому.
2.Погода в данном месте в определенное время суток может быть охарактеризована системой случайных величин: 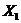 - температура;
- температура; 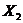 - влажность;
- влажность; 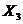 - давление;
- давление; 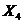 - скорость ветра и т.п.
- скорость ветра и т.п.
Любая СВ 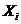 (i = 1,2,...,n) есть функция элементарных событий ω, входящих в пространство элементарных событий Ω (
(i = 1,2,...,n) есть функция элементарных событий ω, входящих в пространство элементарных событий Ω ( 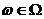 ). Поэтому и многомерная случайная величина есть функция элементарных событий ω:
). Поэтому и многомерная случайная величина есть функция элементарных событий ω: 
т.е. каждому элементарному событию ω ставится в соответствие несколько действительных чисел 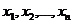 , которые приняли случайные величины
, которые приняли случайные величины 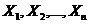 в результате испытания. В этом случае вектор х = (
в результате испытания. В этом случае вектор х = ( 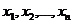 ) называется реализацией случайного вектора Х = (
) называется реализацией случайного вектора Х = ( 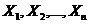 ).
).
Случайные величины 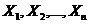 , входящие в систему, могут быть как дискретными (см. выше пример 1), так и непрерывными (пример 2).
, входящие в систему, могут быть как дискретными (см. выше пример 1), так и непрерывными (пример 2).
Закон распределения и функция распределения двух случ величин.
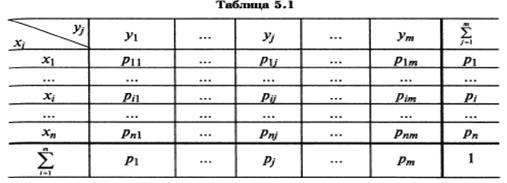 Наиболее полным описанием многомерной СВ является закон ее распределения. При конечном множестве возможных значений многомерной СВ такой закон может быть задан в форме таблицы (матрицы), содержащей всевозможные сочетания значений каждой из одномерных случайных величин, входящих в систему, и соответствующие им вероятности. Так, если рассматривается двумерная дискретная случайная величина (X,Y), то ее двумерное распределение можно представить в виде таблицы (матрицы) распределения (табл. 5.1), в каждой клетке (i,j) которой располагаются вероятности произведения событий
Наиболее полным описанием многомерной СВ является закон ее распределения. При конечном множестве возможных значений многомерной СВ такой закон может быть задан в форме таблицы (матрицы), содержащей всевозможные сочетания значений каждой из одномерных случайных величин, входящих в систему, и соответствующие им вероятности. Так, если рассматривается двумерная дискретная случайная величина (X,Y), то ее двумерное распределение можно представить в виде таблицы (матрицы) распределения (табл. 5.1), в каждой клетке (i,j) которой располагаются вероятности произведения событий 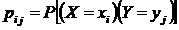 .
.
|
|
|
Так как события 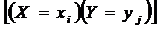 (i = 1,2,...,n; j = 1,2,...,m), состоящие в том, что СВ Х примет значение
(i = 1,2,...,n; j = 1,2,...,m), состоящие в том, что СВ Х примет значение 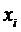 , а СВ Y - значение
, а СВ Y - значение 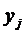 , несовместны и единственно возможны, т.е. образуют полную группу, то сумма их вероятностей равна единице, т.е.:
, несовместны и единственно возможны, т.е. образуют полную группу, то сумма их вероятностей равна единице, т.е.: 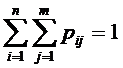
Функцией распределения системы двух сл\в наз ф-я двух аргументов F(x, y), равная в-ти совместного выполнения двух неравенств X<x, Y<y.
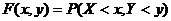
Свойства функции распределения системы двух сл\в:
1) Если один из аргументов стремится к плюс бесконечности, то ф-я распр системы стремится к ф-ии распр одной сл\в, соответствующей другому аргументу.
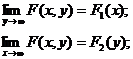
2) Если оба аргумента стремятся к бесконечности, то ф-я распр системы стремится к 1.

3) При стремлении одного или обоих аргументов к минус бесконечности ф-я распр стремится к 0.
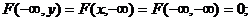
4) Ф-я распр является неубывающей функцией по каждому аргументу.
|
|
|
5) В-ть попадания случайной точки (X, Y) в произвольный прямоугольник со сторонами, параллельными координатным осям, вычисляется по формуле:
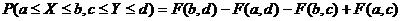
52.П лотность совместного распределения вероятностей непрерывной двумерной случ. величины.
Плотность совместного распределения вероятностей 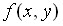 непрерывной двумерной случайной величины (
непрерывной двумерной случайной величины ( 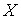 ,
, 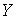 ) – это вторая смешанная частная производная от функции распределения
) – это вторая смешанная частная производная от функции распределения  :
:
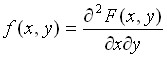 .
.
Геометрически эту функцию можно истолковать как поверхность, которую называют поверхностью распределения.
Зная плотность совместного распределения 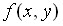 , можно найти функцию распределения
, можно найти функцию распределения  по формуле:
по формуле:
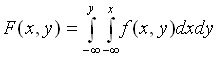
что непосредственно следует из определения плотности распределения двумерной непрерывной случайной величины ( 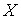 ,
, 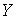 ).
).
Плотность совместного распределения вероятностей 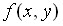 можно рассматривать как предел отношения вероятности попадания случайной точки в прямоугольник (с вершиной в точке
можно рассматривать как предел отношения вероятности попадания случайной точки в прямоугольник (с вершиной в точке 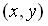 и сторонами
и сторонами 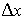 и
и 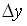 ) к площади этого прямоугольника, когда обе стороны этого прямоугольника стремятся к нулю.
) к площади этого прямоугольника, когда обе стороны этого прямоугольника стремятся к нулю.
Действительно, вероятность попадания случайной точки ( 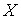 ,
, 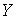 ) в прямоугольник с вершинами
) в прямоугольник с вершинами 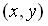 ,
, 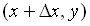 ,
, 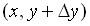 и
и 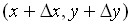 равна:
равна:
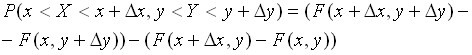
Применив к правой части теорему Лагранжа, получим:
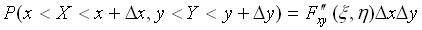
где 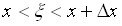 ;
;  . Отсюда:
. Отсюда:
|
|
|
Дата добавления: 2018-05-13; просмотров: 253; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
