Сформулируйте св-ва дисперсии.

1.Дисперсия постоянной величины равна нулю: .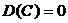

□ . ■

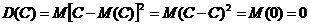2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат: .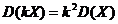

□ Учитывая свойство 2 математического ожидания, получим . ■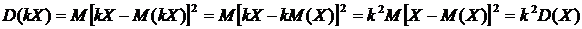

3. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания: 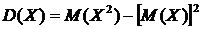(3.16) или 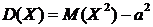где .

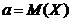□ Пусть М(Х) = а. Тогда D(Х) = М(Х - а)² = М(Х²- 2аХ + а²). Учитывая, что а - величина постоянная, неслучайная, найдем

D(Х) = М(Х)²- 2аМ(Х) + а² = М(Х²) - 2а·а + а² = M(X²) - a².

Это свойство часто используют при вычислении дисперсии. Вычисление по формуле (3.16) дает, например, упрощение расчетов по сравнению с основной формулой (3.11), если значения xi случайной величины - целые, а математическое ожидание, а значит, и разности (xi - а) - нецелые числа.

4. Дисперсия алгебраической суммы конечного числа независимых случайных величин равна сумме их дисперсий: .

□ По свойству 3: 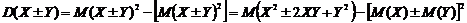. Обозначая 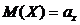, 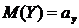и учитывая, что для независимых случайных величин М(ХУ)=М(Х)М(У), получим

.■

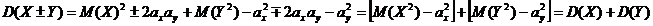Обращаем внимание на то, что дисперсия как суммы, так и разности независимых случайных величин Х и У равна сумме их дисперсий, т.е. .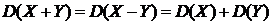

5.Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.

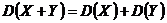
6.Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.

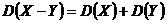
Математическое ожидание, дисперсия, среднее квадратическое отклонение и другие числа, призванные в сжатой форме выразить наиболее существенные черты распределения, называются числовыми характеристиками случайной величины.

Обратим внимание на то, что сама величина Х - случайная, а ее числовые характеристики являются величинами неслучайными, постоянными.

Определение начального и центрального моментов k-го порядка. Каковы простейшие соотношения между ними.

Начальным моментом k-го порядка случ. велич X наз-ся мат. ожидание k-й степени этой величины: ν_k=M(X^k). Для непрерывн случ велич: ν_k=∫х^k φ(x)dx (интеграл от -∞ до +∞). Центральный моментом k-го порядка случ. велич. X наз-тся матю ожидание k-й степени отклонения X от ее мат. ожидания: μ_k=M[X-M(X)]^k. Для непрерывной случ велич: μ_k= ∫(х-М(Х))^k φ(x)dx (интеграл от -∞ до +∞).

Центральный момент первого порядка равен нулю:

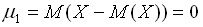
Центральный момент второго порядка представляет собой дисперсию случайной величины :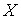

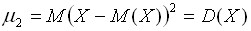
Для дискретных случайных величин:
;

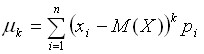
Третий центральный момент μ₃ служит для характер-ки асимметрии распределения. А= μ₃\σ³. Если распред-е симметрично относительно мат. ожидания, то А=0. Отношение центрального момента третьего порядка к среднему квадратическому отклонению в третьей степени называется коэффициентом асимметрии.

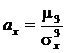
Для характеристики островершинности и плосковершинности распределения используется величина, называемая эксцессом.

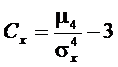
Определение моды и медианы.

Модой дискретной случайной величины называется ее наиболее вероятное значение.

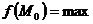
Если многоугольник распределения для дискретной случайной величины имеет два или несколько максимумов, то такое распределение называется двухмодальным или многомодальным.

Если распределение имеет минимум, но не имеет максимума, то оно называется антимодальным.

Определение.Медианой 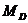случайной величины 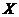называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины.

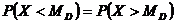
Геометрически медиана – абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам.

Отметим, что если распределение одномодальное, то мода и медиана совпадают с математическим ожиданием.

Дата добавления: 2018-05-13; просмотров: 249; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 7 8 9 10 111213 14 15 16 Следующая ⇒

Мы поможем в написании ваших работ!