ЭТАПЫ СТАНОВЛЕНИЯ СОВРЕМЕННОЙ МАТЕМАТИКИ

Стр 1 из 5Следующая ⇒

МИНИСТЕРСТВО ВНУТРЕННИХ ДЕЛ

ПРИДНЕСТРОВСКОЙ МОЛДАВСКОЙ РЕСПУБЛИКИ

ТИРАСПОЛЬСКИЙ ЮРИДИЧЕСКИЙ ИНСТИТУТ

Им. М.И. КУТУЗОВА

Кафедра оперативно-розыскной деятельности

ЛЕКЦИЯ

по дисциплине «Информатика и информационные технологиив профессиональной деятельности»

специальность 031001.65 - «Правоохранительная деятельность»

ТЕМА №12:«Математические методы обработки информации. Основы теории вероятностей и математической статистики»

Г. Тирасполь, 2014 г.

ПЛАН:

1. Этапы становления современной математики

2. Числа и действия над числами

3. Уравнения и неравенства

4. Функции

5. Основные понятия теории вероятностей

6. Способы определения вероятностей

7. Математическое моделирование

8. Современные информационные технологии анализа и оценки оперативной обстановки деятельности ОВД

Литература:

1. Информатика и математика для юристов: учебник / под ред. С. Я. Казанцева, Н. М. Дубининой – М.: ЮНИТИ-ДАНА, 2012.

2. Информатика базовый курс. 2-е изд. / Под ред. С.В. Симоновича СПб.: Питер, 2011

3. Информационные технологии в юридической деятельности. / Под редакцией профессора П.У. Кузнецова – М.: Юрайт, 2013.

4. Информационные технологии: учебник для вузов. Б.Я. Советов, В.В. Целиховский. – М.: Высшая школа, 2009.

5. Основы правовой информатики (юридические и математические основы информатики): учебное пособие / С. Г. Чубукова, В. Д. Элькин; под ред. М. М. Рассолова. - Изд. 2-е, испр. и доп. - М.: Контракт: ИНФРА-М, 2009.

6. Могилев, А. В. Практикум по информатике: (учебное пособие) / А. В. Могилев, Н. И. Пак, Е.К. Хеннер; под ред. Е. К. Хеннера.- 4-е изд., стер. — М.: Академия, 2008.

7. Информационные технологии в юридической деятельности. / Згадзай О.Э. и др. - М.: Юнити-Дана, 2014.

ВВЕДЕНИЕ

Математика - одна из древнейших наук. Дать краткое определение математики совсем не просто, его содержание будет очень сильно меняться в зависимости от уровня математического образования человека. Попытки определить математику путем перечисления составляющих ее ветвей уводят нас в сторону, поскольку не дают представления о том, что же именно изучает математика и каково ее отношение к окружающему нас миру. Не существует таких явлений природы, технических или социальных процессов, которые были бы предметом изучения математики, но при этом не относились бы к явлениям физическим, биологическим, химическим, инженерным или социальным. Каждая естественнонаучная дисциплина определяется материальной особенностью своего предмета, специфическими чертами той области реального мира, которую она изучает. Для математики же материальный предмет исследования не имеет решающего значения, важен применяемый метод.

Итак, математика изучает не материальные предметы, а методы исследования и структурные свойства объекта исследования, которые позволяют применять к нему некоторые операции (суммирование, дифференцирование и др.). Математический результат обладает тем свойством, что его можно не только применять при изучении какого-то одного определенного явления или процесса, но и использовать для исследования других явлений, физическая природа которых принципиально отличается от ранее рассмотренных.

Кроме математики теоретической существует еще и такое понятие, как прикладная математика. Под ним понимают совокупность всех математических методов и дисциплин, находящих применение за пределами математики.

Математика, прежде чем изучать своими методами какое-нибудь явление, создает его математическую модель, т.е. перечисляет все те особенности явления, которые будут приниматься во внимание. Модель принуждает исследователя выбирать те математические средства, которые позволяют вполне адекватно передать особенности изучаемого явления и его эволюцию.

Конечно, каждая модель огрубляет действительность, и задача исследователя состоит в первую очередь в том, чтобы продолжить модель, передающую, с одной стороны, наиболее полно фактическую сторону дела (как принято говорить, ее физические возможности), а с другой - дающую значительное приближение к действительности. Разумеется, что для одного и того же явления можно предложить несколько математических моделей. Все они имеют право на существование до тех пор, пока не начнет сказываться существенное расхождение модели и действительности.

Вероятно, нет такой области человеческого знания, в которой в той или иной степени не использовались или не могли бы использоваться методы моделирования. Это обусловливается тем, что метод моделирования обладает всеобщностью: моделировать можно любой объект. Принципиальная возможность моделирования объектов любой природы равнозначна принципиальной их познаваемости.

ЭТАПЫ СТАНОВЛЕНИЯ СОВРЕМЕННОЙ МАТЕМАТИКИ

Ясное понимание самостоятельного положения математики как особой науки, имеющей собственный предмет и метод, стало возможным только после накопления достаточно большого фактического материала и возникло впервые в Древней Греции в 6 - 5 вв. до н.э. Развитие математики до этого времени естественно отнести к периоду нарождения математики, а к 6 - 5 вв. до н.э. приурочить начало периода элементарной математики.В течение этих двух первых периодов математического исследования имеют дело почти исключительно с весьма ограниченным запасом основных понятий, возникающих еще на очень ранних ступенях исторического развития в связи с самыми простыми запросами хозяйственной жизни, сводившимися к счету предметов, измерению количества продуктов, площадей земельных участков, определению размеров отдельных частей архитектурных сооружений, измерению времени, коммерческим расчетом и т.п.

Первые шаги механики и физики (за исключением отдельных исследований греческого ученого Архимеда (3 в. До н.э.), требовавших уже начатков исчисления бесконечно малых) могли еще удовлетвориться этим же запасом основных математических понятий. Единственной наукой, которая задолго до широкого развития математического изучения явлений природы в 17 - 18 вв. систематически предъявляла математике свои особые и очень большие требования, была астрономия, целиком обусловившая, например, раннее развитие тригонометрии. Запас понятий, с которым имело дело математика до начала 17 в., составляет и до настоящего времени основу «элементарной математики», преподаваемой в начальной и средней школе.

Наибольшей напряженностью математического творчества отличается первый век Александрийской эпохи (3 в. до н.э.). Этому веку принадлежат Евклид, Архимед, Эратосфен и АполлонийПергский. Сложные гидротехнические сооружения (например, архимедов винт), требование военной техники (метательные машины Архимеда), запросы мореплавания (исследования Архимеда о равновесии и устойчивости плавающих тел) развитие геодезии и картографии (определение Эратосфеном размеров земного шара), а также разработка точных астрономических измерений и вычислений (Юлианское приближение к длине года, равное 365 1/4 дней), наконец развитие механики и оптики - все это поставило перед математикой множество новых задач. 3 в. до н.э. явился веком плодотворного соединения соответствующего этим требованиям стремительного развития математики вширь с глубиной теоретической мысли. В частности, возникший из прикладных нужд интерес к приближенному измерению величин и приближенным вычислениям не привел математиков 3 в. до н.э. к отказу от математической строгости. Все многочисленные приближенные извлечения корней и даже все астрономические вычисления производились ими с точным указанием границ погрешности, по типу знаменитого архимедова определения длины окружности в форме безукоризненно доказанных неравенств

где r - длина окружности с диаметром d. Это отчетливое понимание того, что приближенная математика не есть «нестрогая» математика, было позднее надолго забыто.

В своих «Началах» Эвклид собрал и подверг окончательной логической переработки достижения предыдущего периода в области геометрии. Вместе с тем в «Началах» же Эвклид впервые заложил основы систематической теории чисел, доказывая бесконечность ряда простых чисел и строя законченную теорию делимости. Наконец, «Начала» содержат во второй, шестой и десятой книгах своеобразную геометрическую замену алгебры, позволяющую в геометрической форме не только решать квадратные уравнения, но и производить сложные преобразования квадратичных иррациональных выражений.

В 17 в. Новые запросы естествознании и техники заставляют математиков сосредоточить свое внимание на создании методов, позволяющих математически изучать движение, процессы изменения величин, преобразования геометрических фигур (при проектировании и т.п.).

С употреблением переменных величин в аналитической геометрии французского ученого Р. Декарта и создания дифференциального и интегрального исчисления начинается период математики переменных величин, который можно условно назвать также периодом «высшей математики». Естественно впрочем, что не в этот ни следующий период не прекращалась дальнейшее развитие элементарной математики.

В начале 19 века происходит новое значительное расширение области приложения математического анализа. Если до этого времени основными отделами физики, требовавшими большого математического аппарата, оставалась механика и оптика, то теперь к ним присоединилась электродинамика, теория магнетизма и термодинамика. Получают широкое развитие важнейшие разделы механики непрерывных сред, из которых только гидродинамика несжимаемой идеальной жидкости была создана еще в 18 в. Д.Бернулли, Эйлером, Д’Аламбером и Лагранжем. Быстро растут и математические запросы техники. В начале 19 в. это вопросы термодинамики. В качестве основного аппарата новых областей механики и математической физики усилено разрабатывается теория дифференциальных уравнений с частными производными и особенно теория потенциала. В этом направлении работает большинство крупных аналитиков начала и середины века (немецкий математик К.Гаусс, французский математик Ж.Фурье, С.Пуассон, О.Коши, немецкий математик П.Дирихле, английский математик Д.Грин, русский математик М.В.Остроградский). М.В.Остроградский заложил основы вариационного исчисления для функций нескольких переменных, нашел знаменитую формулу преобразования тройных интегралов в двойные и ее n-мерное обобщение.

Несмотря на господствующее в естествознании начала 19 века механического убеждения в возможности описать все природные явления дифференциальными уравнениями, под давлением запросов практики получает значительное дальнейшее развитие теория вероятностей. Лаплас и Пуассон создают с этой целью новый мощный аналитический аппарат. В России применением теории вероятностей к приемочному контролю и статистики занимаются М.В.Остроградский и В.Я.Буняковский; П.Л.Чебышев дает строгое обоснование элементов теории вероятностей и доказывает свою знаменитую теорему, объединившую в одной общей формулировке известные ранее формы закона большого числа.

Дальнейшее расширение круга количественных отношений и пространственных форм, изучаемых математикой, привело к необходимости отнестись к процессу расширения предмета математических исследований сознательно, поставив перед собой задачу систематического изучения с достаточно общей точки зрения возможных типов количественных отношений и пространственных форм. Создание русским математиком Н.И.Лобачевским его «воображаемой геометрии», получившей в последствии вполне реальные применения, были первым значительным шагом в это направлении. XX в. принес новые методы математического исследования практических задач: теорию случайных процессов, теорию графов, функциональный анализ, оптимальное управление, линейное и нелинейное программирование.

ЧИСЛА И ДЕЙСТВИЯ НАД ЧИСЛАМИ

1,2,3,...,8,...,424,...к..., где к - любое целое положительное число, называются натуральными числами. Целые положительные и отрицательные, а также дробные числа вида 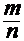где m и n - целые числа, причем n¹ 0, именуют числами рациональными. Всякое рациональное число можно представить конечной или, в соответствующих случаях, периодической бесконечной десятичной дробью.

Наряду с рациональными существуют иррациональные, представляющие собой непериодические бесконечные дроби. Таковы, например, 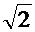= 1,4142....; p = 3,1415..., е = 2,718281...

Рациональные и иррациональные числа составляют класс действительных (вещественных) чисел.

Развитие алгебры, связанное с необходимостью извлечения квадратных корней из отрицательных чисел, потребовало введение чисел нового вида, названных комплексными. Комплексные числа представляют собой пары чисел вида a + bi, где i² = -1, то есть i = 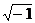. В комплексном числе a и b - обыкновенные действительные числа, а bi именуется мнимой частью комплексного числа.

В некоторых случаях оказывается необходимым при действиях с обыкновенными вещественными числами, не обращать внимание на их знак. Тогда используется понятие об абсолютной величине или о модуле действительного числа. Модуль действительного числа обозначают символом ½a½. Согласно определению, например, ½-2½ = ½2½ = 2; ½-56½ = 56 и т.д.

Число (точнее говоря - переменную величину) называют бесконечно большим и обозначают символом ¥, если желают выразить, что оно превосходит любое другое число. Этим обозначением оно не фиксируется, как объект расчетов и к символу ¥нельзя применять обычные правила вычислений.

Число называют бесконечно малым, если желают выразить, что оно имеет абсолютную величину меньшую, чем любое произвольно заданное (положительное) число. Для обозначения этого понятия не пользуются специальным символом, заменяя его записями вида или , читая первое из выражений так: «предел величины при x, стремящемся к бесконечности, равен нулю», а второе - «предел величины при x, стремящемся к нулю, равен бесконечности». Символ lim означает «предел», «лимит».

Совокупность действительных чисел образует линию, называемую «числовой осью», на которой каждое число служит координатой, определяющей положение точки, соответствующей числу. Числовая ось - прямая, то есть одномерное числовое пространство.

На числовой оси могут быть выбраны: начальная точка отсчета, условно принимаемое за положительное направления и масштаб. Можно считать, например, что начальная точка отсчета - «ноль», направо от нее размещены точки, отображающие положительные числа («положительное направление оси»), налево - точки, соответствующие отрицательным числам («отрицательное направление оси»).

Если некоторые объекты или свойства их представляют рядом отдельных, дискретных значений чисел, то положение каждого такого числа в своем ряду может быть обозначено индексом. Пусть, например, ряд является последовательностью чисел 15; 4,3; 2; 0,5 и и.д. Символически его можно записать так: а₁, а₂, а₃, а₄, ..., где а₁ = 15, а₂ = 4,3, а₃ = 2, а₄ = 0,5 ... Здесь числа 1, 2, 3, 4, ... определяют места членов ряда и называются индексами. Любой член ряда можно обозначить символом а_i, причем индекс i укажет его «номер» в последовательности ряда. В некоторых случаях, когда следует проводить расчеты с группами последовательно расположенных в ряд чисел, пользуются обозначениями «от а_i, до а_j». Если указать, например, « от i = 1 до j = 8», то это означает, что следует брать группу членов ряда от 1-го до 8-го включительно.

Для условного обозначения чисел, значение которых заранее известны, обычно применяют первые буквы латинского алфавита, а для неизвестных чисел - последние (x, y, z, u, ...). Некоторыми буквами принято обозначать константы ( p = 3,14... - отношение длины окружности к диаметру, e = 2,71... - основание натуральных логарифмов, g = 9,81 м.сек²= величина ускорения тела, падающего в пустоте под действием земного притяжения, и т.д.).

Над числами наиболее часто выполняют следующие операции: сложение, вычитание, умножение и деление, возведение в степень, извлечение корня, логарифмирование. Правила 4-х арифметических действий общеизвестны, поэтому напомним только об операциях возведения в степень, извлечения корня и логарифмирования.

При возведении в степень число («основание степени») умножается само на себя столько раз, сколько указано «показателем степени». Возведение во вторую степень (в квадрат) - умножение числа самого на себя, в третью степень (в куб) - умножение квадрата числа еще раз на исходное число и т.д. Такого рода перемножение, представляющее собой возведение числа в целую положительную степень, осуществляется просто. При возведении числа в целую, но отрицательную степень, результат представляется дробью, в числителе которой помещается единица, а в знаменателе - возводимое в степень число с тем же, но положительным показателем степени.

Извлечение корня - действие обратное возведению в степень. Так, например, извлечение квадратного корня - это нахождение числа, квадрат которого равен числу, находящемуся под знаком корня.

УРАВНЕНИЯ И НЕРАВЕНСТВА

Математические записи зависимостей между неизвестными и известными величинами называются уравнениями.

Различают уравнения по нескольким признакам, в том числе:

- по числу неизвестных - на уравнения с одним, двумя, тремя и т.д. неизвестными;

- по значениям показателей степени, в которых фигурируют неизвестные, - на уравнения первого порядка или линейные, квадратные, кубические, четвертой степени («биквадратные») и т.д.;

- по характеру представления неизвестных величин - на алгебраические, для решения которых достаточно использовать средства алгебры, тригонометрические, решаемые средствами тригонометрии, дифференциальные, к решению которых необходимо применять методы дифференциального исчисления, и др.

Выражение y = f (x) представляет собой математическую запись зависимости значений переменной y от x, характеризуемую условным обозначением «f» и читается так: «игрек равно эф от икс», или «игрек функция от х». Здесь х именуется аргументом или независимой переменной.

Уравнение с одной переменной, если все его члены находятся в левой части, а в правой части - нуль, может быть записано в общем виде в форме f(x) = 0, с двумя переменными f(x, y) = 0, с тремя - f(x, y, z) = 0 и т.д. Запись «y = f(x)» представляет собой отображение результата решения относительно y уравнения с двумя неизвестными х и у. Конкретный смысл вида функции f при этом не раскрывается.

Составить уравнение - это значит выразить в математической форме связь между искомыми и известными величинами.

Важнейшие принципы решения систем уравнений можно показать на примере решения систем двух уравнений первой степени (линейных) с двумя неизвестными.

Система двух уравнений с двумя неизвестными в общем виде записывается так:

ì a₁x + b₁y = c₁

îa₂x + b₂y = c₂

Система может иметь одно решение, бесконечное множество решений или не иметь ни одного решения. При нахождении решения системы уравнений можно воспользоваться следующими методами:

а) исключением одной неизвестной;

б) подстановкой;

в) при помощи вычисления определителей.

ФУНКЦИИ

При функциональной зависимости между двумя переменными x и y, каждому значению, которое может принимать одна из них, соответствует одно или несколько определенных значений другой.

Эту связь можно записать в символах в виде:

y = f(x)

где x - аргумент (независимая переменная), причем интервал допустимых значений x - область определения функции;

y - значение функции (зависимая переменная); а символ представляет характер функциональной зависимости y от х.

Не всегда можно функциональную зависимость предоставить в виде конкретной формулы или, если это удается, формула иногда оказывает неудобной для вычислений. В таких случаях пользуются табличными или графическими способами задания функции.

Способы задания функции. Существует несколько способов задания функции.

а) аналитический способ, если функция задана формулой вида у = f (х). Все функции, рассмотренные в примерах 1-5 заданы аналитически.

б) табличный способ состоит в том, что функция задается таблицей, содержащей значения х и соответствующие значения f (х), например, таблица логарифмов.

в) графический способ, состоит в изображении графика функции – множество точек (х, у) плоскости, абсциссы которых есть значения аргумента х, а ординаты – соответствующие им значения функции у = f (х).

Линейные функции.Если величина y изменяется пропорционально х, то функциональная зависимость между ними выражается уравнением

y = ax

где а - постоянная - коэффициент пропорциональности или, так называемый, угловой коэффициент.

График прямой пропорциональности y = ax есть прямая линия которая проходит через начала координат и образует с осью абсцисс угол a. Тангенс угла a равен а (tga=a).

Линейная функция одной переменной в общем случае имеет вид

y = ax + b

где a и b - постоянные величины, где b¹ 0.

Переменные x и y входят в это выражение в первой степени. График такой функциональной зависимости есть прямая линия, не проходящая через начало координат.

Линейная функция двух переменных x и y имеет вид

z = ax + by + c

где a, b и c - постоянные величины.

Графически эта функция отображается плоскостью в трехмерном пространстве.

Если линейная функция имеет n аргументов х₁, х₂, х₃, ... х_n, то она имеет вид

F = a_nx_n + a_n-1x_n-1 + ... + a₂x₂ + a₁x₁ + a₀,

где а₀, а₁, а₂, ..., а_n - постоянные величины.

Линейные функции применяются, например, при описании зависимостей, необходимых для расчета оптимальных маршрутов сбора личного состава, при патрулировании для охраны объектов, при анализе статистической информации о состоянии преступности в регионах ( метод наименьших квадратов, корреляционный метод) и др.

Гиперболическая функция.Если функциональная зависимость между переменными величинами x и yвыражается

Где а - постоянная величина, то переменные x и y обратно пропорциональны и график функции имеет вид кривой именуемой гиперболой.

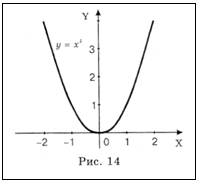Квадратичная функция. Эта функция имеет вид

y = ax² + bx + c

где a, b и c - постоянные величины, а ¹ 0, называется квадратичной.

Степенная функция.Функция вида

y = axⁿ,

где a, b и c - постоянные величины, называется степенной. Ранее рассмотренные функции являются частными видами степенной функции при n =1, n = 2, n = -1.

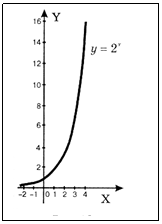Показательная функция.Функция вида

y = a^x,

где а - постоянная величина, называется показательной. При рассмотрении показательной функции число а берется положительным, т.к. при а<0 значения функци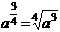и или 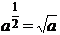и др. Не были бы действительными числами, а числами мнимыми.

При а = 1 график этой функции представляет прямую линию . При а>1 кривая, выражающая показательную функцию, показывает рост ее значения, а при а < 1 - понижение.

При а = е, где е = 2,718 ... (основание натурального логарифма).

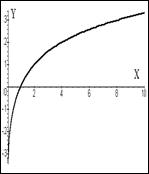
Логарифмическая функция.Функции видаy = log_ax,где а - постоянное положительное число называется логарифмической.

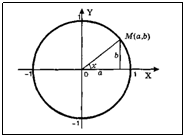Тригонометрические функции. При решении задач, связанных с построением геометрических фигур (треугольника и др.), используются тригонометрические функции. В прямоугольном треугольнике отношения различных пар сторон называются тригонометрическими функциями величин его углов. Этосинус, косинус, тангенс, котангенс (sina, cosa, tga, ctga), причем последние четыре просто выражаются через синус и косинус:

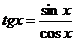Синус, косинус и тангенс, котангенс периодическими функциями с периодом 2П, и для них:

sinx = sin(x + 2л) = sin(x + 4л) = ... = sin(x + 2πk),

cosx = cos(x + 2л) = cos(x + 4л) = ... = cos(x + 2πk),

где k — любое целое число.

Периодичность — важнейшее специфическое свойство тригонометрических функций. Другие функции — степенная, показательная и логарифмическая — периодическими не являются. С помощью тригонометрических функций описываются самые разнообразные периодические процессы, происходящие в живой и неживой природе: колебательные и вращательные движения, волновые явления, движение планет, биологические ритмы и т.д.

Сложная функция.(суперпозиция функций).

Пусть функция у = f(u) есть функция от переменной u, определенная на множестве U с областью значений – У, а переменная u = φ(х) функция от переменной х, определенной на множестве Х с областью значения U. Тогда заданная на множестве Х функция у = f(φ(x)) называется сложной функцией (функцией от функций). Например, у = lgsin 3х. Эту сложную функцию от х можно расписать, как цепочку простых функций: у= lg u, u = sin t, t = 3x.

Понятия элементарной функции.Функции построенные из основных элементарных функций с помощью конечного числа алгебраических действий называются элементарными.

Например, у = 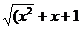)/(sin²х+3) или у = 2 - tg х.

Определение предела функции. Пусть функция у = f(х) определена в некоторой точке а, кроме, может быть, самой этой точки.

Число b называется пределом функции f(х) при х стремящемся к а, если для любого сколь угодно малого, наперед заданного ε>0 существует такое δ>0, что для всех х таких, что |х-а|<δ выполняется неравенство |f(x) - b|<ε.

x→a

В компактном виде это определение можно записать lim f(x) = b.

(lim – сокращенное слово limit(предел)).

Читается так: предел f(x) при х стремящемся к а равен b.

Дата добавления: 2018-04-15; просмотров: 1415; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 Следующая ⇒

Мы поможем в написании ваших работ!