Металлический волновод прямоугольного сечения. Структура волны ТМ поляризации

Волновод – это канал, имеющий резкие границы, вдоль которого распространяется электромагнитное излучение. Рассмотрим металлический волновод прямоугольного сечения.

Рассмотрим волноводную моду, у которой проекция магнитного поля на ось z равна нулю, а проекция электрического поля на ось z отлична от нуля. 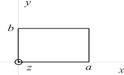Волноводную моду с такой поляризацией называют TM – волной. Анализ показывает, что для нахождения TM мод нужно использовать электрический потенциал Герца . Запишем уравнение Гельмгольца и граничные условия для рассматриваемой конфигурации.

Уравнение решается методом разделения переменных, и результат имеет следующий вид. 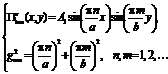решение.

Находим дисперсионное соотношение для моды .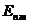

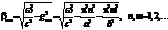 TM – волны будут описываться следующими уравнениями.

;

25.Цилиндрический металлический волновод. Дисперсионное соотношение для волноводных мод ТЕ поляризации

Волновод – это канал, имеющий резкие границы, вдоль которого распространяется электромагнитное излучение. Металлический волновод – это металлическая труба, произвольного сечения, внутри которой распространяется электромагнитная волна Волноводную моду, у которой проекция электрического поля на ось z равна нулю, а проекция магнитного поля на ось z отлична от нуля называют ТЕ волной

Уравнение Гельмгольца для магнитного потенциала Герца в цилиндрических координатах принимает следующий вид.

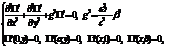
 Уравнение решается методом разделения переменных. В результате получаем следующее решение уравнения  Граничные условия для ТЕ волноводной моды выглядят следующим образом. 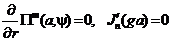 Здесь штрих у функции Бесселя означает взятие первой производной.

Решение уравнения Гельмгольца с граничным условием для магнитного потенциала Герца примет следующий вид.

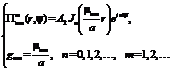
Находим дисперсионное соотношение для моды .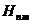

Цилиндрический металлический волновод. Дисперсионное соотношение для волноводных мод ТМ поляризации

Цилиндрическую систему координат выберем, так как показано на Рис.

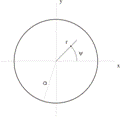Уравнение Гельмгольца для электрического и магнитного потенциалов Герца в цилиндрических координатах принимает следующий вид.

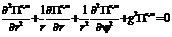  (4.105)Уравнение решается методом разделения переменных. В результате получаем следующее решение уравнения (4.105).   (4.106) Здесь 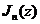- функция Бесселя 1-ого рода, порядка n.

Рассмотрим TM волноводные моды. Граничное условие (4.81) теперь примет следующий вид.  (4.107)

Для решения последнего уравнения (4.107) нужно знать корни функции Бесселя. Корни функции Бесселя 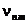 находятся из следующего уравнения.

                                (4.108)

Приведем некоторые значения корней функции Бесселя.

      (4.109)

На Рис.32 приведены графики двух функций Бесселя.

Рис.31

Если нули функции Бесселя известны, то решение уравнения Гельмгольца (4.105) с граничным условием (4.107) для электрического потенциала Герца примет следующий вид.

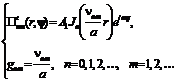                         (4.110)

Формулы (4.110) определяют структуру TM волноводной моды в металлическом волноводе круглого сечения.

Из уравнений (4.110) и (4.80) находим дисперсионное соотношение для моды .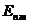

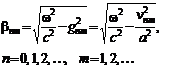                                 (4.111)

Частоты отсечки для волновода с круглым сечением определяются следующим выражением.

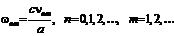                         (4.112)

Используя найденный электрический потенциал Герца  для моды 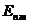 можно построить картину линий электрического и магнитного поля в плоскости xy. Заметим что в формулах (4.110), потенциал Герца записан в комплексном виде. Для построения линий электрического и магнитного поля нужно взять действительную часть от него. Поэтому линии магнитного поля совпадают со следующими эквипотенциальными линиями.

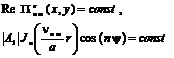                                   (4.113)

На Рис.33 показана картина линий электрического и магнитного поля для моды  с радиусом a = 1. Сплошные линии здесь линии магнитного поля, стрелки показывают направление электрического поля.

Рис.33

На Рис.34 показана картина линий электрического и магнитного поля для моды 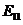 с радиусом a = 1. Сплошные линии здесь линии магнитного поля, стрелки показывают направление электрического поля.

 

27  Двухпроводная длинная линия.

Идеальность проводника означает, что внутри металла электромагнитное поле равно нулю 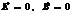. Вне проводника на его поверхности выполняются следующие граничные условия.

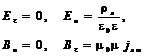                                   (6.16)

Здесь – поверхностная плотность электрического заряда, - проекция вектора поверхностной плотности тока 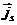 на ось m.

Изобразим сечение двухпроводной линии плоскостью z = const Рис.72.

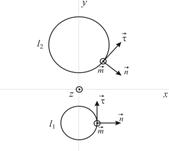
Рис.72.

На Рис.72 две металлические поверхности изображены в плоскости xy двумя контурами l₁, l₂. На двух металлических поверхностях изображены единичные векторы нормальный и касательный 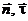. Второй касательный вектор  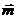направлен к нам. Исследуя соотношения (6.8), (6.13), приходим к следующему выводу. Для выполнения граничных условий 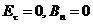требуется наложить следующее условие на потенциал Герца.

                                                (6.17)

Это означает, что на металлической поверхности, в каждой точке контура l потенциал Герца имеет постоянное значение. Рассмотрим два оставшихся граничных условия.

                                        (6.18)

Граничные условия (6.18) позволяют найти поверхностный заряд и поверхностный ток на металлических поверхностях двухпроводной линии.

Возьмем отрезок двухпроводной линии длиной Dl в направлении оси z. Тогда заряд на первом проводе Dq₁ и заряд на втором проводе Dq₂ будут определяться интегралами:

                                     (6.19)

Токи, текущие вдоль оси Oz по эти двум проводам, будут определяться следующими интегралами:

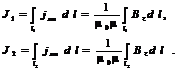                                        (6.20)

Разберемся с величиной зарядов Dq₁ , Dq₂ на проводах длинной линии. Для удобства перейдем к скалярному потенциалу. Во всей бесконечной области, исключая проводники, решаем уравнение Лапласа (6.14) для потенциала j. На поверхностях двух проводников потенциал имеет постоянные значения равные j ₁ и j ₂.

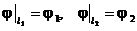                                               (6.21)

Если потенциалы j ₁ и j ₂ на проводниках заданы, то задача имеет однозначное решение. Далее, зная скалярный потенциал, можно найти электрическое и магнитное поле по формулам (6.8). Эти формулы можно переписать через потенциал в следующем виде.

28.

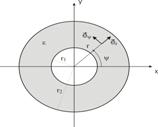
Рис.75.

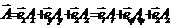Таким образом, вектор может характеризоваться тремя проекциями или на орты декартовой системы координат или на орты цилиндрической системы координат.

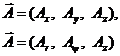                                                (6.33)

Приведем формулы, по которым вычисляет градиент в цилиндрической системе координат.

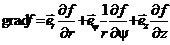                                       (6.34)

Дивергенция в цилиндрических координатах будет иметь следующий вид.

                                   (6.35)

Для ротора в цилиндрических координатах существует следующая формула.

      (6.36)

Наконец, действие оператора Лапласа в цилиндрической системе координат определяется следующей формулой.

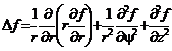                                (6.37)

Исследуем структуру электромагнитного поля в кабеле. Уравнение Лапласа (6.12) в цилиндрической системе координат примет вид.

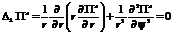                               (6.38)

Учитывая цилиндрическую симметрию кабеля, проходим к выводу, что потенциал Герца не должен зависеть от угла y. Поэтому уравнение (6.38) упрощается.

                                               (6.39)

Решение уравнения (6.39) имеет простой вид.

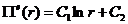                                        (6.40)

Здесь C _{1, C 2} произвольные константы, которые должны определяться из граничных условий.

Теперь найдем электрическое и магнитное поле в кабеле. В цилиндрической системе координат они примут вид.

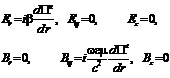                               (6.41)

При выводе формул (6.41) учитывалось, что для продольного волнового числа b справедливо соотношение.

Как было показано выше, в длинных линиях между потенциалом Герца и скалярным потенциалом существует линейная связь.

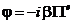
Скалярный потенциал в поперечном сечении кабеля удовлетворяет уравнению Лапласа. Поэтому решение для скалярного потенциала будет иметь вид аналогичный формуле (6.40).

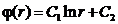                                               (6.42)

Далее, электрическое и магнитное поля будут выражаться через потенциал следующим образом.

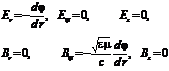                              (6.43)

Подставляя (6.42) в (6.43) находим электрическое и магнитное поле.

                                    (6.44)

Найдем поверхностный заряд на внутреннем и внешнем цилиндрах кабеля по формулам (6.19). Находим заряд на внутреннем цилиндре.

               (6.45)

Здесь было учтено, что вектор нормали  на поверхности внутреннего цилиндра направлен вдоль вектора 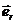, смотри Рис.72 и Рис.75.

Находим заряд на внешнем цилиндре.

                     (6.46)

Здесь мы учли, что вектор нормали  на поверхности внешнего цилиндра направлен в противоположную сторону вектора 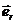, смотри Рис.72 и Рис.75.

Сравнивая формулы (6.45) и (6.46) находим, что заряды на жиле и оплетке кабеля равны по величине и противоположны по знаку. Таким образом, на внутреннем цилиндре и внешнем цилиндре, на отрезке длинной Dl вдоль оси z находятся заряды.

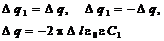
29  Рассмотрим отрезок кабеля длиной Dl. Найдем заряд Dq₁ на поверхности внутреннего цилиндра и заряд на поверхности внешнего цилиндра Dq₂. Для этого вначале найдем поверхностную плотность заряда с помощью граничных условий (6.18). Используя явный вид электрического поля (6.53) получаем следующий результат.

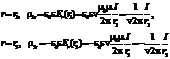Так как поверхностные плотности заряда (6.70) являются постоянными величинами, заряды на цилиндрических поверхностях найдем, умножив плотность заряда на величину поверхности цилиндра.

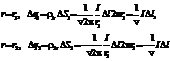                 Из формул (6.71) следует что, на внутреннем и внешнем цилиндрах отрезка кабеля находятся заряды одинаковые по величине и разные по знаку.

                                    Таким образом, отрезок кабеля является заряженным цилиндрическим конденсатором, емкость которого DC определяется следующим выражением.

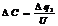                                                (Используя формулы (6.71) для заряда и формулу (6.54) для напряжения, находим емкость отрезка кабеля.

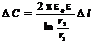
В дальнейшем нам понадобится погонная емкость кабеля 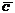, или емкость единицы длины кабеля. Погонная емкость кабеля определяется следующим выражением.

---

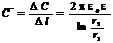
Дата добавления: 2018-04-04; просмотров: 589; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!