Металлический волновод. Структура э/м поля. Граничные условия
Задача нахождения электромагнитного поля волноводной моды сводится к решению уравнений Гельмгольца для проекций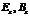 
электрического и магнитного поля, в области D , ограниченной контуром l. Полученные решения 
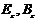затем подставляются в формулы (4.22) и (4.23) из которых находятся остальные проекции электрического 
и магнитного поля 
.
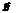Уравнения Гельмгольца имеют определенные решения, если на контуре l заданы некоторые граничные условия для проекций 
. Эти граничные условия должны быть такими, чтобы найденные в результате электрическое и магнитное поле удовлетворяло граничным условиям (4.10) в каждой точке металлической поверхности волновода, через которую проходит контур l. Поэтому главной задачей здесь является выбор правильных граничных условий на контуре l для проекций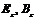 
. Рассмотрим волноводную моду, у которой проекция магнитного поля на ось z равна нулю, а проекция электрического поля на ось z отлична от нуля. 
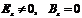(4.27)
Волноводную моду с такой поляризацией называют TM – волной. То есть, волной с поперечным магнитным полем (transverse magnetic field). Другое название такой моды это E – волна. То есть волна, у которой продольная составляющая электрического поля отлична от нуля.
Подставляем (4.27) в уравнения (4.24) и (4.25) получаем формулы для нахождения остальных проекций электрического и магнитного поля TM - волноводной моды.
(4.28)
Исследуем граничные условия (4.10). Рассмотрим условие, где касательная составляющая электрического поля на поверхности проводника равняется нулю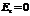 
. Выразим вектор электрического поля через проекции в декартовой системе координат. 
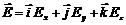(4.29)
|
|
|
Спроектируем выражение (4.29) на единичный вектор 
. 
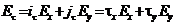(4.30)
Подставим проекции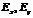 
из формул (4.28) в уравнение (4.30). В результате получим следующее соотношение.
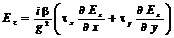(4.31)
С другой стороны вычислим производную по направлению вектора : 
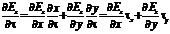(4.32)
Сравнивая формулы (4.31) и (4.32) получаем следующее соотношение.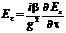 
(4.33)
Так как рассматриваемое граничное условие имеет вид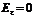 
, из соотношения (4.33) получаем следующее уравнение: 
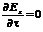(4.34)
Уравнение (4.34) означает, что проекция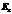 
вдоль контура l имеет постоянное значение: 
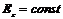(4.35)
При выводе граничных условий (4.10) вектор мог быть любым касательным вектором. Поэтому вместе с граничным условием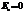 
должно выполняться также граничное условие 
. На Рис.19 показано, что направление единичного вектора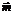 
и оси z совпадают. Поэтому имеет место, следующее соотношение: 
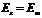(4.36)
Таким образом, приходим к выводу, сто константа в соотношении (4.35) должна равняться нулю. В результате получаем следующее граничное условие на контуре l.
|
|
|
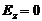(4.37)
Убедимся что граничное условие (4.37) приводит также к выполнению еще одного граничного условия из системы граничных условий (4.10). Покажем, что нормальная составляющая магнитного поля на поверхности проводника равняется нулю 
.
Выразим вектор магнитного поля через проекции в декартовой системе координат: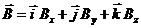 
(4.38)
Спроектируем выражение (4.38) на единичный вектор 
: 
(4.39)
Подставим проекции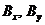 
из формул (4.28) в уравнение (4.39). В результате получим следующее соотношение: 
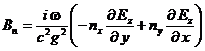(4.40)
Единичные векторы и взаимно перпендикулярны, поэтому проекции вектора можно выразить через проекции вектора . Используя взаимную ориентацию векторов на Рис.19, получаем следующую связь между векторами и .
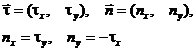(4.41)
Подставляем соотношения (4.41) в уравнение (4.40). В результате получаем следующее выражение.
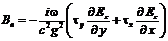(4.42)
Используем формулу (4.32) и переписываем соотношение (4.42) в следующем виде.
|
|
|
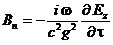(4.43)
Учитываем формулу (4.34) и получаем из (4.43) нужное граничное условие.
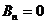(4.44)
Таким образом, для нахождения TM – волноводной моды выбрано корректное граничное условие (4.37).
Рассмотрим волноводную моду, у которой проекция электрического поля на ось z равна нулю, а проекция магнитного поля на ось z отлична от нуля.
(4.45)
Волноводную моду с такой поляризацией называют TE – волной. То есть, волной с поперечным электрическим полем (transverse electric field). Другое название такой моды это H – волна. То есть волна, у которой продольная составляющая магнитного поля отлична от нуля.
Подставляем (4.45) в уравнения (4.24) и (4.25) получаем формулы для нахождения остальных проекций электрического и магнитного поля TE - волноводной моды.
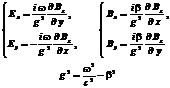(4.46)
Исследуем граничные условия (4.10). Рассмотрим условие, где нормальная составляющая магнитного поля на поверхности проводника равняется нулю 
.
Воспользуемся выражением (4.39) для проекции магнитного поля 
, и подставим туда выражения для проекций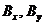 
из уравнений (4.46).
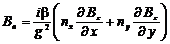(4.47)
|
|
|
С другой стороны вычислим производную по направлению вектора .
(4.48)
Сравнивая формулы (4.47) и (4.48) получаем следующее соотношение.
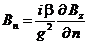(4.49)
Так как рассматриваемое граничное условие имеет вид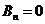 
, из соотношения (4.49) получаем следующее условие.
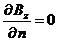(4.49)
Условие (4.49) означает, что в любой точке контура l производная по направлению нормали от проекции магнитного поля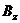 
равна нулю.
Убедимся что граничное условие (4.49) приводит также к выполнению еще одного граничного условия из системы граничных условий (4.10). Покажем, что касательная составляющая электрического поля на поверхности проводника равняется нулю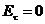 
.
Воспользуемся выражением (4.30) для проекции электрического поля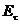 
, и подставим туда выражения для проекций 
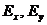из уравнений (4.46).
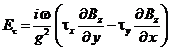(4.50)
С помощью формул (4.41) выражаем проекции касательного вектора через проекции нормального вектора . В результате получаем следующее выражение.
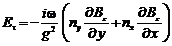(4.51)
Выражение в скобках преобразуем с помощью формулы (4.48). В результате получаем следующую формулу.
(4.52)
Учитываем формулу (4.49) и получаем из (4.52) нужное граничное условие.
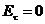(4.53)
Таким образом, для нахождения TE – волноводной моды выбрано корректное граничное условие (4.49).
Приведем сводку формул для нахождения электрического и магнитного поля в TM – волноводной моде.
(4.54)
Аналогично, приведем сводку формул для нахождения электрического и магнитного поля в TE – волноводной моде.
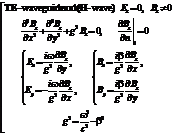(4.55)
21.Планарный металлический волновод. Структура волны ТЕ поляризации.
Волновод – это канал, имеющий резкие границы, вдоль которого распространяется электромагнитное излучение. Металлический волновод – это металлическая труба, произвольного сечения, внутри которой распространяется электромагнитная волна
Если у металлического волновода прямоугольного сечения одна из сторон много больше другой, то такой волновод называют планарным волноводом.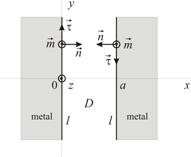 
Волновод однороден в направлении оси y.( 
) . Рассмотрим волноводную моду, у которой проекция электрического поля на ось z равна нулю, а проекция магнитного поля на ось z отлична от нуля. Волноводную моду с такой поляризацией называют TЕ – волной.
Сводка формул для нахождения электрического и магнитного поля в TЕ – волноводной моде. Теперь запишим эти формулы для планарного волновода (учтя граничные условия).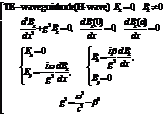 
Уравнение Гельмгольца в системе (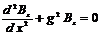 
) с указанными граничными условиями легко решается. Результат такого решения имеет следующий вид.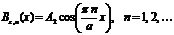 
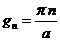. Подставляем величину 
в систему получаем дисперсионное соотношение для волноводной моды 
. 
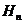Условие существования моды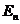 
(подкоренное выражение больше нуля) 
; 
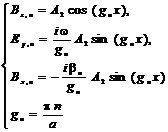
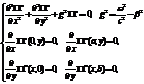
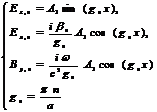
22.Планарный металлический волновод. Структура волны ТМ поляризации. Волновод – это канал, имеющий резкие границы, вдоль которого распространяется электромагнитное излучение. Металлический волновод – это металлическая труба, произвольного сечения, внутри которой распространяется электромагнитная волна
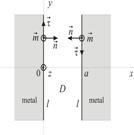
Если у металлического волновода прямоугольного сечения одна из сторон много больше другой, то такой волновод называют планарным волноводом. Волновод однороден в направлении оси y.( ) . Рассмотрим волноводную моду, у которой проекция магнитного поля на ось z равна нулю, а проекция электрического поля на ось z отлична от нуля. Волноводную моду с такой поляризацией называют TM – волной. Сводка формул для нахождения электрического и магнитного поля в TM – волноводной моде. Теперь запишим эти формулы для планарного волновода .
Уравнение Гельмгольца(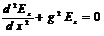 
)в системе с указанными граничными условиями легко решается. Результат такого решения имеет следующий вид.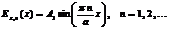 
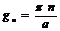. Подставляем величину в систему получаем дисперсионное соотношение для волноводной моды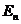 
. 
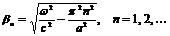Условие существования моды 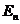(подкоренное выражение больше нуля) .
Конечные формулы отличных от нуля проекции электрического и магнитного поля волноводной TM моды.
23. Металлический волновод прямоугольного сечения. Структура волны ТЕ поляризации.Волновод – это канал, имеющий резкие границы, вдоль которого распространяется электромагнитное излучение. Рассмотрим металлический волновод прямоугольного сечения.
Рассмотрим волноводную моду, у которой проекция электрического поля на ось z равна нулю, а проекция магнитного поля на ось z отлична от нуля.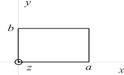 
Волноводную моду с такой поляризацией называют TЕ – волной. Анализ показывает, что для нахождения TЕ мод нужно использовать магнитный потенциал Герца 
. Запишем уравнение Гельмгольца и граничные условия для рассматриваемой конфигурации.
Уравнение решается методом разделения переменных, и результат имеет следующий вид.
решения.
Находим дисперсионное соотношение для моды Hnm .
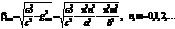Индексы n и m начинаются с нуля. Однако одновременно равняться нулю они не могут. Иначе электрическое и магнитное поле такой моды будет рано нулю. Поэтому моды H00 не существует. TЕ – волны будут описываться следующими уравнениями. 
; 
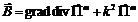
Дата добавления: 2018-04-04; просмотров: 455; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!