Определение полной абсолютной и полной относительной погрешности прямых измерений

⇐ ПредыдущаяСтр 4 из 17Следующая ⇒

Абсолютная и относительная погрешность прямых измерений зависят от класса точности прибора и умения определять погрешность взвешивания. Прежде чем говорить о том, как вычисляется погрешность, необходимо уточнить определения. Прямым называется измерение, при котором происходит непосредственное считывание результата с приборной шкалы. Когда мы пользуемся термометром, линейкой, вольтметром или амперметром, то всегда проводим именно прямые измерения, так как применяем непосредственно прибор со шкалой. Есть два фактора, которые влияют на результативность показаний: Погрешностью приборов. Погрешностью системы отсчета.

Расчет погрешности измерений

Измерения называются прямыми,если значения величин определяются приборами непосредственно (например, измерение длины линейкой, определение времени секундомером и т. д.). Измерения называютсякосвенными, если значение измеряемой величины определяется посредством прямых измерений других величин, которые связаны с измеряемой определенной зависимостью.

Случайные погрешности при прямых измерениях

Абсолютная и относительная погрешность.Пусть проведеноNизмерений одной и той же величиныxв отсутствии систематической погрешности. Отдельные результаты измерений имеют вид:x₁,x₂, …,x_N. В качестве наилучшего выбирается среднее значение измеренной величины:.

Абсолютной погрешностьюединичного измерения называется разность вида:.

Среднее значение абсолютной погрешности Nединичных измерений:

называется средней абсолютной погрешностью.

Относительной погрешностьюназывается отношение средней абсолютной погрешности к среднему значению измеряемой величины:

11-16

Косвенные - это измерения, при которых искомую величину определяют на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям, т.е. измеряют не собственно определяемую величину, а другие, функционально с ней связанные. Значение измеряемой величины находят путем вычисления по формуле , где - искомое значение косвенно измеряемой величины; 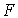- функциональная зависимость, которая заранее известна, - значения величин, измеренных прямым способом.3. Основные характеристики измерений

Выделяют следующие основные характеристики измерений:

1) метод, которым проводятся измерения;

2) принцип измерений;

3) погрешность измерений;

4) точность измерений;

5) правильность измерений;

6) достоверность измерений.

Метод измерений– это способ или комплекс способов, посредством которых производится измерение данной величины, т. е. сравнение измеряемой величины с ее мерой согласно принятому принципу измерения.

Существует несколько критериев классификации методов измерений.

1. По способам получения искомого значения измеряемой величины выделяют:

1) прямой метод (осуществляется при помощи прямых, непосредственных измерений);

2) косвенный метод.

2. По приемам измерения выделяют:

1) контактный метод измерения;

2) бесконтактный метод измерения.

Контактный метод измеренияоснован на непосредственном контакте какой-либо части измерительного прибора с измеряемым объектом.

При бесконтактном методе измеренияизмерительный прибор не контактирует непосредственно с измеряемым объектом.

3. По приемам сравнения величины с ее мерой выделяют:

1) метод непосредственной оценки;

2) метод сравнения с ее единицей.

Метод непосредственной оценкиоснован на применении измерительного прибора, показывающего значение измеряемой величины.

Метод сравнения с меройоснован на сравнении объекта измерения с его мерой.

Принцип измерений– это некое физическое явление или их комплекс, на которых базируется измерение.

Погрешность измерения– это разность между результатом измерения величины и настоящим (действительным) значением этой величины.

Точность измерений– это характеристика, выражающая степень соответствия результатов измерения настоящему значению измеряемой величины.

Правильность измерения– это качественная характеристика измерения, которая определяется тем, насколько близка к нулю величина постоянной или фиксировано изменяющейся при многократных измерениях погрешности (систематическая погрешность).

Достоверность измерений– это характеристика, определяющая степень доверия к полученным результатам измерений.

ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА Графическое представление результатов обладает большой на- глядностью и информативностью. Графики экспериментальных зависи- мостей позволяют легко визуально определять характер зависимости, судить о величине разброса экспериментальных данных по сравнению с предсказаниями теории и т.д. Отличительной особенностью графиков, изображающих физиче- ские зависимости, является размерный характер отложенных по осям величин. Для того чтобы графики, построенные при выполнении лабора- торных работ, были максимально информативными, необходимо со- блюдать определенные правила их построения. Основные требования, предъявляемые к построению графиков 1. Графики строят на бумаге форматом 14×14 см с помощью линейки и карандаша либо специальных компьютерных программ для построения графиков (например, MS Excel, Origin, Mathematica и др.). Готовый график должен быть вложен в отчет по лабораторной работе. 2. На координатных осях должны быть указаны обозначения откладываемых величин и единицы их измерения. 3. Начало координат при необходимости может не совпадать с нулевыми значениями величин. Его выбирают таким образом, чтобы поверхность бумаги была использована максимально. 4. Экспериментальные точки изображаются четко и крупно в виде кружков, крестиков, разноцветных точек и т.п. 5. Масштабные деления на координатных осях следует нано- сить равномерно. Координаты экспериментальных точек на осях не ука- зывают, а линии, определяющие эти координаты, не проводят. 6. Масштаб выбирают таким образом, чтобы: 47 a. Кривая была равномерно растянута вдоль обеих осей (если график представляет собой прямую, то угол ее наклона к осям должен быть близок к 450 ). b. Положение любой точки можно было определить легко и бы- стро. Масштаб считается удобным, если в одном масштабном делении (миллиметре или сантиметре), нанесенном на оси графика, содержится одна или две (пять, десять, пятьдесят и т. д.) единиц измеренной величины. 7. Учитывая, что экспериментальные данные содержат опреде- ленную случайную погрешность, кривую (прямую), изображающую экспериментальную зависимость, следует проводить не по точкам, а между ними – так, чтобы количество точек по обе стороны от нее было одинаковым. Кривая должна быть плавной. 8. На графике необходимо отложить погрешность измерения величин (доверительный интервал). Делается это с помощью вертикаль- ных или горизонтальных отрезков ( , ) симметрично расположен- ных относительно экспериментальных точек.

Наиболее типичные ошибки при построении графиков Пусть требуется построить график зависимости пути от времени = ( )tfS при равномерном движении тела. Результаты измерений при- ведены в таблице 4. 48 Таблица 4 t, c 10 12 14 15 16 18 19 22 S, м 20 23 30 31 34 34 38 43 На рис. 14 показаны основные наиболее типичные ошибки, допус- каемые студентами при построении графиков. 5 15 20 20 30 38 S Рис. 14 Ошибки, допущенные при построении графика, изображенного на рис. 14: 1. Неправильно выбраны направления осей координат: время t является независимой переменной (аргументом) и должно быть отложе- но по оси абсцисс (по горизонтали), а зависимая переменная (функция) – путь S по оси ординат (по вертикали). 2. На оси ординат не указана отложенная величина (время t) и единицы ее измерения (с), а на оси абсцисс – единицы измерения пути S (м). 3. Площадь графика использована не полностью. Из эксперимен- тальных данных, приведенных в таблице 4, не следует, что оси коорди- 49 нат должны начинаться с нулевой отметки, поэтому начало координат можно сместить и за счет этого увеличить масштаб. 4. Экспериментальные точки не выделены. 5. На оси ординат нанесены не масштабные деления, а координа- ты экспериментальных точек, по оси абсцисс масштабные деления на- несены неравномерно. 6. Неправильно выбрано начало координат и неудачный (слиш- ком мелкий масштаб). Поэтому график сжат по оси абсцисс и его чтение затруднено. 7. Неправильно соединены экспериментальные точки: зависи- мость пути от времени при равномерном движении заведомо линейна, и график должен представлять прямую линию. На рис. 15 представлен график этой же зависимости S = f(t), по- строенный правильно.

ПОЛУЧЕНИЕ АНАЛИТИЧЕСКИХ ЗАВИСИМОСТЕЙ Пусть в результате эксперимента получены значения двух изме- ряемых величин: y1, y2, y3, … yn и x1, x2, x3,…. xn, которые связаны неко- торой функциональной зависимостью ) y = f (x , вид которой заранее не известен. На примере линейной зависимости рассмотрим несколько ме- тодов, позволяющих получить неизвестную аналитическую функцию. 50 Графический метод получения параметров аналитической зависимости По имеющимся экспериментальным данным y1, y2, y3, … yn и x1, x2, x3,…. xn построим график зависимости ) y = f (x . По виду графика (с учетом погрешности измерений) определим, можно ли имеющуюся за- висимость считать линейной. Если изучаемую зависимость можно счи- тать линейной, то она может быть выражена формулой y = ax + b, где a и b − неизвестные коэффициенты, подлежащие определению. Обязательными условиями применения данного метода являют- ся следующее: начало отсчета по обеим осям начинается с нуля; обе оси имеют равномерный масштаб. На построенном графике зависимости ) y = f (x проводят сглажи- вающую прямую до пересечения с осью ординат. Прямая проводится на глаз как можно ближе к экспериментальным точкам.

16.Аналитический способ представления результатов измерения

Как правило, выполняются следующие виды измерений:

- измерения величин, характеризующих параметры электрических сигналов (амплитуда, частота, период, мощность), коэффициенты модуляции по различным аргументам; определение коэффициентов амплитуды и формы сигналов; определение среднего и среднего квадратичного значений;

- измерения параметров аппаратуры, определяющих условия передачи информации (усиление, затухание, переходные помехи и отношение сигнал/шум, линейные и нелинейные искажения и др.);

- измерения с целью градуировки, регулировки и поверки технических средств;

- измерения параметров каналов и трактов, определение характера и места повреждения на линиях связи. В любом случае проводится математическая обработка измерительной информации с целью уменьшения и исключения погрешностей;

- измерения параметров аппаратуры, характеризующих входные и выходные параметры.

Согласно ИСО 5725, «...правильность метода измерений имеет смысл в тех случаях, когда можно получить представление об истинном значении измеряемой характеристики (свойства). При этом правильность метода измерений можно исследовать сопоставлением принятого опорного значения измеряемой величины с уровнем результатов измерений, полученных этим методом». Синонимом термина «правильность» является «систематическая погрешность».

В зависимости от характера проявления погрешностей результирующее значение определяется по-разному. Предположим, что техническое средство измерений содержит ряд разных функциональных устройств, которые характеризуются наличием систематических и случайных составляющих погрешностей.

Если обозначить систематические составляющие погрешностей α, тогда для оценки результирующей погрешности прибора «вход—выход» принято использовать простое арифметическое сложение:

∑α. =α1 + α2 + α3 + ... + с учетом знаков «плюс» или «минус».

Поскольку такие погрешности частично компенсируются, то остаточная сумма а может быть учтена путем введения поправочного коэффициента, значение которого определяется в результате поверки прибора и его предварительной калибровки. Обычно поправочные коэффициенты прилагаются в документации к прибору в виде графиков и таблиц в зависимости от режимов работы приборов и пределов измерения.

Для обработки и представления результатов измерений применяют различные методы, в том числе с использованием описательной статистики, графических методов, анализа измерений и т.д.

17.Систематизация законов измерения с помощью законов распределения

18 Замена опытного распределения результатов измерений теоретическим законом

19 Проверка гипотез о принятии теоретического закона распределения

Обычно сущность проверки гипотезы о законе распределения ЭД заключается в следующем. Имеется выборка ЭД фиксированного объема, выбран или известен вид закона распределения генеральной совокупности. Необходимо оценить по этой выборке параметры закона, определить степень согласованности ЭД и выбранного закона распределения, в котором параметры заменены их оценками. Пока не будем касаться способов нахождения оценок параметров распределения, а рассмотрим только вопрос проверки согласованности распределений с использованием наиболее употребительных критериев.

Критерий хи-квадрат К. Пирсона

Использование этого критерия основано на применении такой меры (статистики) расхождения между теоретическим F(x) и эмпирическим распределением F_п(x), которая приближенно подчиняется закону распределения c². Гипотеза Н₀ о согласованности распределений проверяется путем анализа распределения этой статистики. Применение критерия требует построения статистического ряда.

Итак, пусть выборка представлена статистическим рядом с количеством разрядов y. Наблюдаемая частота попаданий в i-й разряд n_i. В соответствии с теоретическим законом распределения ожидаемая частота попаданий в i-й разряд составляет F_i. Разность между наблюдаемой и ожидаемой частотой составит величину (n_i–F_i). Для нахождения общей степени расхождения между F(x) и F_п(x) необходимо подсчитать взвешенную сумму квадратов разностей по всем разрядам статистического ряда

(3.7)

Величина c² при неограниченном увеличении n имеет распределение хи-квадрат (асимптотически распределена как хи-квадрат). Это распределение зависит от числа степеней свободы k, т.е. количества независимых значений слагаемых в выражении (3.7). Число степеней свободы равно числу y минус число линейных связей, наложенных на выборку. Одна связь существует в силу того, что любая частота может быть вычислена по совокупности частот в оставшихся y–1 разрядах. Кроме того, если параметры распределения неизвестны заранее, то имеется еще одно ограничение, обусловленное подгонкой распределения к выборке. Если по выборке определяются f параметров распределения, то число степеней свободы составит k=y–f–1.

Очевидно, что чем меньше расхождение между теоретическими и эмпирическими частотами, тем меньше величина критерия. Область принятия гипотезы Н₀ определяется условием c²<c²(k; a), где c²(k; a) – критическая точка распределения хи-квадрат с уровнем значимости a. Вероятность ошибки первого рода равна a, вероятность ошибки второго рода четко определить нельзя, потому что существует бесконечно большое множество различных способов несовпадения распределений. Мощность критерия зависит от количества разрядов и объема выборки. Критерий рекомендуется применять при n>200, допускается применение при n>40, именно при таких условиях критерий состоятелен (как правило, отвергает неверную нулевую гипотезу).

Пример 3.1.Проверить с помощью критерия хи-квадрат гипотезу о нормальности распределения случайной величины, представленной статистическим рядом в табл. 2.4 при уровне значимости a=0,05.

Решение . В примере 2.3 были вычислены значения оценок моментов:

m₁=27,51, m₂=0,91, s=0,96.

На основе табл. 2.4 построим табл. 3.2, иллюстрирующую расчеты.

Таблица 3.2

Номер интервала, i	1	2	3	4	5	6
n_i	5	9	10	9	5	6
x_i	26,37	26,95	27,53	28,12	28,70	бесконечность
F(x_i)	0,117	0,280	0,5 08	0,737	0,892	1
D F_i	0,117	0,166	0,228	0,228	0,1 5 5	0,108
F_i	5,148	7,304	10,032	10,032	6,820	4,752
(n_i - F_i)²/F_i	0,004	0,394	0,0001	0,1062	0,486	0,328

В этой таблице:

ni – частота попаданий элементов выборки в i-й интервал;

xi – верхняя граница i-го интервала;

F(xi) – значение функции нормального распределения;

DFi – теоретическое значение вероятности попадания случайной величины в i-й интервал

Fi=DFi*n – теоретическая частота попадания случайной величины в i-й интервал;

(ni–Fi)²/Fi – взвешенный квадрат отклонения.

Для нормального закона возможные значения случайной величины лежат в диапазоне от минус до плюс бесконечности, поэтому при расчетах оценок вероятностей крайний левый и крайний правый интервалы расширяются до минус и плюс бесконечности соответственно. Вычислить значения функции нормального распределения можно, воспользовавшись стандартными функциями табличного процессора или полиномом наилучшего приближения.

Сумма взвешенных квадратов отклонения c₂=1,32. Число степеней свободы

k = 6–1–2=3,

так как уклонения связаны линейным соотношением

кроме того, на уклонения наложены еще две связи, ибо по выборке были определены два параметра распределения. Критическое значение c²(3; 0,05)=7,815 определяется по табл. П.3 приложения. Поскольку соблюдается условие c²<c²(3; 0,05), то полученный результат нельзя считать значимым и гипотеза о нормальном распределении генеральной совокупности не противоречит ЭД.

Критерий А.Н. Колмогорова

Для применения критерия А.Н. Колмогорова ЭД требуется представить в виде вариационного ряда (ЭД недопустимо объединять в разряды). В качестве меры расхождения между теоретической F(x) и эмпирической F_n(x) функциями распределения непрерывной случайной величины Х используется модуль максимальной разности

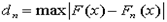
(3.8)

А.Н. Колмогоров доказал, что какова бы ни была функция распределения F(x) величины Х при неограниченном увеличении количества наблюдений n функция распределения случайной величины

асимптотически приближается к функции распределения

Иначе говоря, критерий А.Н. Колмогорова характеризует вероятность того, что величина

не будет превосходить параметр l для любой теоретической функции распределения. Уровень значимости a выбирается из условия

в силу предположения, что почти невозможно получить это равенство, когда существует соответствие между функциями F(x) и F_n(x). Критерий А.Н. Колмогорова позволяет проверить согласованность распределений по малым выборкам, он проще критерия хи-квадрат, поэтому его часто применяют на практике. Но требуется учитывать два обстоятельства.

1. В соответствии с условиями его применения необходимо пользоваться следующим соотношением

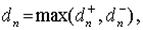
где

2. Условия применения критерия предусматривают, что теоретическая функция распределения известна полностью – известны вид функции и значения ее параметров. На практике параметры обычно неизвестны и оцениваются по ЭД. Но критерий не учитывает уменьшение числа степеней свободы при оценке параметров распределения по исходной выборке. Это приводит к завышению значения вероятности соблюдения нулевой гипотезы, т.е. повышается риск принять в качестве правдоподобной гипотезу, которая плохо согласуется с ЭД (повышается вероятность совершить ошибку второго рода). В качестве меры противодействия такому выводу следует увеличить уровень значимости a, приняв его равным 0,1 – 0,2, что приведет к уменьшению зоны допустимых отклонений.

Пример 3.2.Проверить с помощью критерия А.Н. Колмогорова гипотезу о том, что ЭД, представленные в табл. 2.3, подчиняются нормальному распределению при уровне значимости a=0,1.

Решение. Исходные данные и результаты вычислений сведены в табл. 3.3. Необходимые вычисления можно провести с использованием табличного процессора: значение эмпирической функции распределения F_n(x_i)=i/44; значения теоретической функции F(x_i) – это значение функции нормального распределения в точке x_i.

Таблица 3.3

i	1	2	3	4	5	6	7	8	9	10	11
x_i	25,79	25,98	25,98	26,12	26,13	26,49	26,52	26,60	26,66	26,69	26,74
Fn(x_i)	0,023	0,046	0,068	0,091	0,114	0,136	0,159	0,182	0,204	0,227	0,250
F(x_i)	0,036	0,055	0,055	0,073	0,075	0,144	0,151	0,170	0,188	0,196	0,211
d_n⁺	0,014	0,009	0,013	0,018	0,038	0,008	0,008	0,012	0,016	0,032	0,039
d_n^-	0,036	0,032	0,010	0,005	0,016	0,031	0,014	0,011	0,006	0,009	0,016

i	12	13		14		15		16		17		18		19		20		21		22
x_i	26,85	26,90		26,91		26,96		27,02		27,11		27,19		27,21		27,28		27,30		27,38
Fn(x_i)	0,273	0,296		0,318		0,341		0,364		0,386		0,409		0,432		0,455		0,477		0,500
F(x_i)	0,246	0,263		0,267		0,284		0,305		0,337		0,371		0,378		0,406		0,412		0,447
d_n⁺	0,027	0,032		0,051		0,057		0,059		0,050		0,038		0,054		0,049		0,065		0,053
d_n^-	0,004	0,010		0,028		0,034		0,036		0,027		0,015		0,031		0,026		0,042		0,031
i	23		24		25		26		27		28		29		30		31		32		33
x_i	27,40		27,49		27,64		27,66		27,71		27,78		27,89		27,89		28,01		28,10		28,11
Fn(x_i)	0,523		0,546		0,568		0,591		0,614		0,636		0,659		0,682		0,705		0,727		0,750
F(x_i)	0,456		0,492		0,555		0,561		0,583		0,610		0,656		0,656		0,701		0,731		0,735
d_n⁺	0,067		0,053		0,013		0,030		0,031		0,026		0,003		0,026		0,003		0,004		0,015
d_n^-	0,044		0,031		0,010		0,007		0,008		0,003		0,019		0,003		0,020		0,027		0,008
i	34		35		36		37		38		39		40		41		42		43		44
x_i	28,37		28,38		28,50		28,63		28,67		28,90		28,99		28,99		29,03		29,12		29,28
Fn(x_i)	0,773		0,795		0,818		0,841		0,864		0,886		0,909		0,932		0,955		0,977		1,000
F(x_i)	0,817		0,819		0,851		0,879		0,888		0,928		0,939		0,940		0,944		0,954		0,968
d_n⁺	0,044		0,024		0,032		0,038		0,024		0,042		0,030		0,008		0,010		0,024		0,032
d_n^-	0,067		0,046		0,055		0,061		0,047		0,064		0,053		0,031		0,013		0,001		0,009

В данном примере максимальные значения d_n⁺ и d_n^- одинаковы и равны 0,067. Из табл. П.1 при a=0,1 найдем l=1,22. Для n=44 критическое значение

0,184.

Поскольку величина max d_n=0,067 меньше критического значения, гипотеза о принадлежности выборки нормальному закону не отвергается.

Критерий Р. Мизеса

В качестве меры различия теоретической функции распределения F(x) и эмпирической F_n(x) по критерию Мизеса (критерию w²) выступает средний квадрат отклонений по всем значениям аргумента x

(3.9)

Статистика критерия

(3.10)

При неограниченном увеличении n существует предельное распределение статистики nw_n². Задав значение вероятности a можно определить критические значения nw_n²(a). Проверка гипотезы о законе распределения осуществляется обычным образом: если фактическое значение nw_n² окажется больше критического или равно ему, то согласно критерию Мизеса с уровнем значимости a гипотеза Н_О о том, что закон распределения генеральной совокупности соответствует F(x), должна быть отвергнута.

Дата добавления: 2018-02-28; просмотров: 1772; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!