Д-зета функция Римана и Формула Эйлера-Маклорена
№1 Ряд 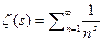
1) Первым шагом в исследовании данной функции является нахождение её значений от чётных положительных аргументов. Для этого рассмотрим формулу Муавра 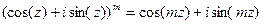 где
где 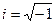 мнимая единица. Раскрывая левую часть по формуле Ньютона и приравнивая коэффициенты при
мнимая единица. Раскрывая левую часть по формуле Ньютона и приравнивая коэффициенты при 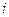 получим что
получим что 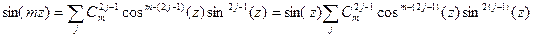 положим
положим 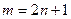 тогда
тогда 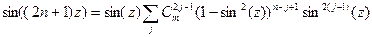 далее положим что
далее положим что
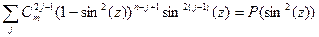 тогда
тогда 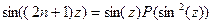 так как
так как
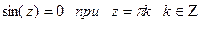 а
а 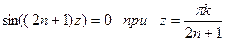 то и
то и 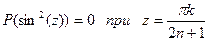 а значит
а значит 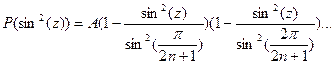
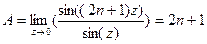 тогда сделав замену
тогда сделав замену 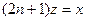 будем иметь
будем иметь
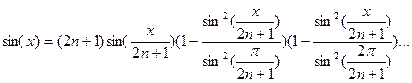 тогда если положить
тогда если положить 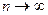 будем иметь
будем иметь 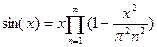
2) По ранее найденному, имеем 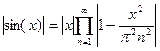 тогда логарифмируя получим что
тогда логарифмируя получим что
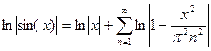 далее дифференцируя будем иметь
далее дифференцируя будем иметь 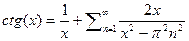 используя связь между тригонометрическими и гиперболическими функциями
используя связь между тригонометрическими и гиперболическими функциями 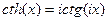 будем иметь
будем иметь 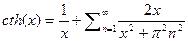 далее умножим оби части равенства на
далее умножим оби части равенства на 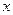 и разложим функцию в ряд
и разложим функцию в ряд 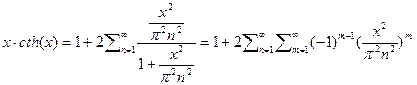 и переставляя суммы местами будем иметь
и переставляя суммы местами будем иметь 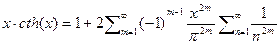
3) Рассмотрим функцию 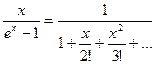 положим. что
положим. что 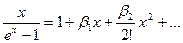 тогда поскольку
тогда поскольку 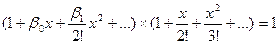 будем иметь
будем иметь
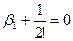
 и вообще
и вообще 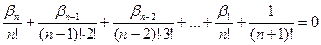 или
или 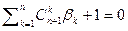 то есть
то есть  те самые числа Бернулли, которые появились в
те самые числа Бернулли, которые появились в
параграфе №2 тогда 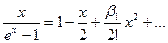 или, перенеся
или, перенеся 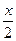 влево,
влево,
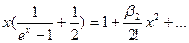 или
или 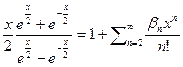 таким образом
таким образом 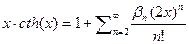
4) Тогда приравняв коэффициенты при одинаковых степенях 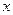 в двух представлениях функции
в двух представлениях функции 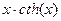 получим, что
получим, что 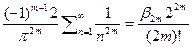 откуда получим, что
откуда получим, что
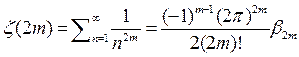
5) Рассмотрим ряд 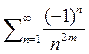 очевидно что
очевидно что 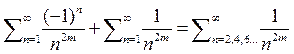 а поскольку
а поскольку 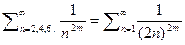 следовательно
следовательно 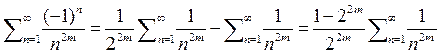 а значит
а значит
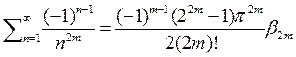
6) Рассмотрим ряд 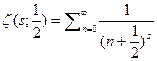 далее
далее 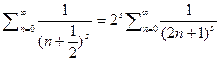 затем возьмём сумму
затем возьмём сумму 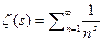 и вычтем из неё сумму
и вычтем из неё сумму 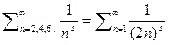 окажется, что
окажется, что 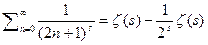 а значит
а значит 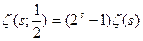 то есть
то есть
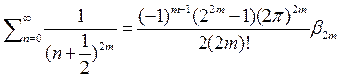 рассмотрим теперь функцию
рассмотрим теперь функцию
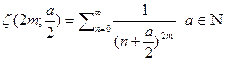 и а нечётно тогда перепишем в виде
и а нечётно тогда перепишем в виде
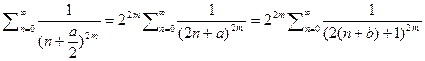 где
где 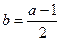 тогда заменяя
тогда заменяя 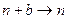 сумма станет равной
сумма станет равной 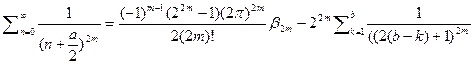 или в итоге получим
или в итоге получим
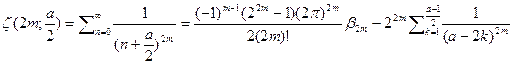
7) Примеры сумм:
а) 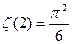 б)
б) 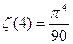 в)
в) 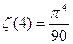 г)
г) 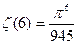 д)
д) 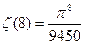 е)
е) 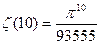
ж) 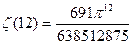 з)
з) 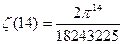 и)
и) 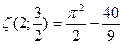 и.т.д.
и.т.д.
|
|
|
№2 Суммы через числа Бернулли
1) Ранее было показано, что если имеется последовательность 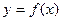 где
где 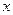 номер элемента тогда
номер элемента тогда 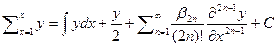 где
где  числа Бернулли
числа Бернулли
2) Рассмотрим ряд 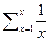 Этот ряд расходится. Попробуем найти его конечную сумму, для этого найдём несколько производных
Этот ряд расходится. Попробуем найти его конечную сумму, для этого найдём несколько производных 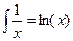
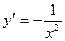
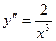
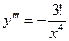 …
… 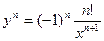
а значит 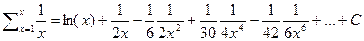 для определения постоянной
для определения постоянной 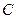 воспользуемся тем что для больших
воспользуемся тем что для больших 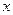 ряд справа быстро сходится откуда например для
ряд справа быстро сходится откуда например для 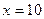 будем иметь
будем иметь 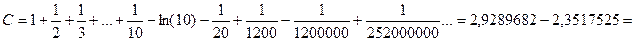
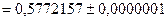 таким образом
таким образом
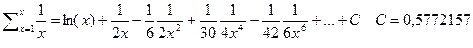 данный ряд является асимптотическим и при больших
данный ряд является асимптотическим и при больших 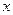
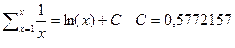 вычисленная нами постоянная
вычисленная нами постоянная 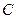 - так называемая постоянная Эйлера.
- так называемая постоянная Эйлера.
2) Рассмотрим n! будем иметь 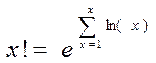 рассмотрим сумму
рассмотрим сумму 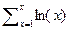
тогда 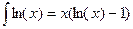
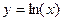
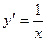
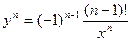 а значит
а значит
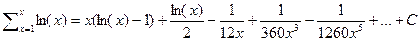 таким образом получим
таким образом получим 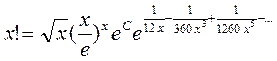 далее
далее 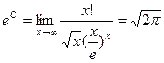 следовательно
следовательно
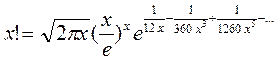 это так называемаяформула Стирлинга.
это так называемаяформула Стирлинга.
Считая, функцию справа непрерывной найдём что 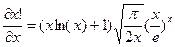 для
для 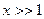
3) Вновь вернёмся к Д-зете функции Римана и найдём общую формулу для произвольного аргумента 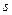 . Для этогонайдём производные
. Для этогонайдём производные 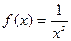 равные
равные 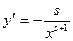
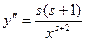 …
…
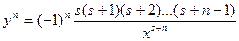 а значит
а значит 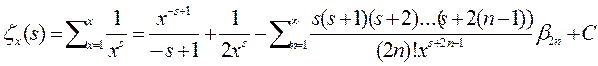
Рассмотрим данный ряд при различных значениях 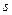
а) Пусть 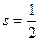 тогда
тогда 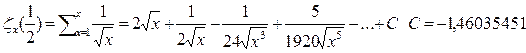
действительно 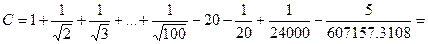
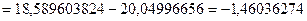 относительная ошибка
относительная ошибка 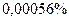
б) Пусть 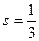 тогда
тогда
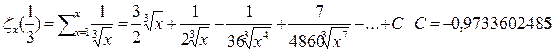
в) Пусть 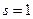 тогда
тогда
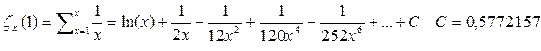
г) Пусть 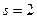 тогда
тогда
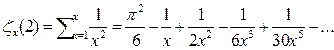 уже при
уже при 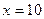 ошибка при сложении 3 членов ряда в 6 знаке после запятой.
ошибка при сложении 3 членов ряда в 6 знаке после запятой.
д) Пусть 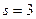 тогда
тогда
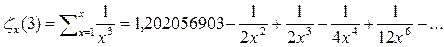
4) Очевидно чтоесли в (8) положить 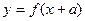 достаточно будет везде к
достаточно будет везде к 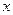 прибавить
прибавить 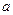 и тогда снова получится верная формула но с новой константой.
и тогда снова получится верная формула но с новой константой.
|
|
|
5) Рассмотрим ряд 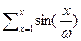 тогда
тогда 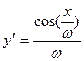
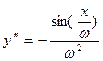 а значит
а значит
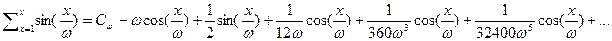 или
или
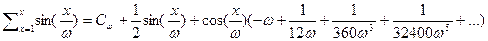
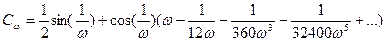 если положить
если положить 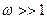 то будем иметь
то будем иметь 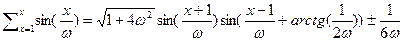
6) Рассмотрим ряд 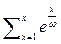 очевидно что
очевидно что 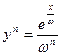 а значит
а значит
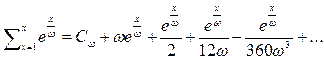 или
или
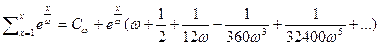 где
где
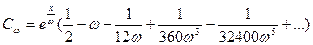
Литература
Дата добавления: 2015-12-21; просмотров: 19; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
