Преобразование рядов
№1 Преобразование рядов по Эйлеру
1) Очень часто бывает трудно или вовсе невозможно получить формулу суммы ряда поэтому особую роль играет преобразование рядов по которое во многих случаях позволяет найти или точную формулу суммы ряда или заменяет его быстросходящимся рядом с той же суммой. Пусть дан сходящийся ряд S(x)= 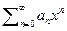 тогда, произведём следующую замену, полжем
тогда, произведём следующую замену, полжем 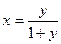 или
или 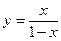
Тогда так как 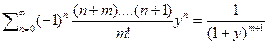 , тогда
, тогда 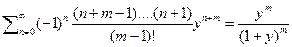 далее подставляя вместо xn его представление в виде ряда, и соберём коэффициенты при одинаковых степенях y получим:
далее подставляя вместо xn его представление в виде ряда, и соберём коэффициенты при одинаковых степенях y получим:


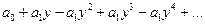
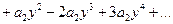
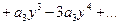
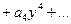
таким образом  замечая что коэффициенты при степенях
замечая что коэффициенты при степенях 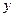 есть первые, вторые … разности получим
есть первые, вторые … разности получим
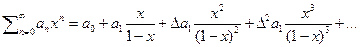 (8)
(8)
или для знакочередующего ряда
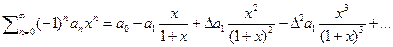 (9)
(9)
Это преобразование носит имя Эйлера и позволяет найти сумму любой последовательности с конечными разностями. То есть по сути формула (8) является полным аналогом формулы (3) и на неё распространяются те же свойства.
2) Используя результат (№3,§1,?1) получим что
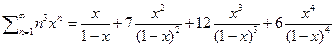
3) С помощью преобразования Эйлера можно находить и конечные суммы действительно возьмём ряд S(x)= 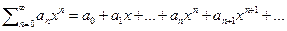 далее посчитаем сумму этого ряда и вычтем из неё сумму
далее посчитаем сумму этого ряда и вычтем из неё сумму 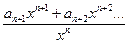 умноженную на
умноженную на 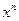 в итоге получим
в итоге получим
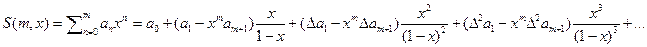 или для знакочередующего ряда
или для знакочередующего ряда 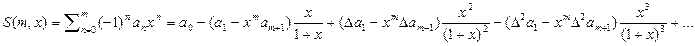
№2 Двойные ряды(Сумма по Эйлеру)
1) Теперь произведём обобщение преобразования Эйлера на функции отличные от 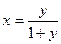 Пусть имеется ряд
Пусть имеется ряд 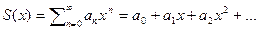 тогда образуем ряд
тогда образуем ряд 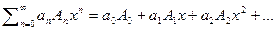 далее предположим что его сумма равна
далее предположим что его сумма равна
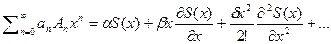 тогда поскольку
тогда поскольку
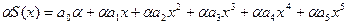
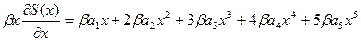
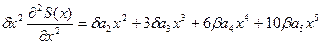 сравнивая коэффициенты в двух суммах получим, что;
сравнивая коэффициенты в двух суммах получим, что;
|
|
|
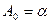
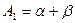
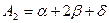
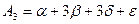
 откуда
откуда 
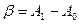
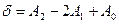 … а значит
… а значит
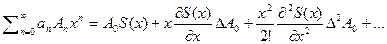
2) Очевидно, что преобразование Эйлера получается при S(x)= 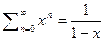
§ 3 Вычисление числовых рядов с переходом к функциональным
№1 Ряды, сводящиеся к элементарным функциям
Как было сказано ранее многие числовые ряды могут быть сведены к функциональным переходом 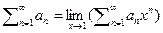 , а сумму соответствующих функциональных рядов можно получить используя операции дифференциального исчисления.
, а сумму соответствующих функциональных рядов можно получить используя операции дифференциального исчисления.
1) Ряд вида 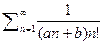 поскольку
поскольку 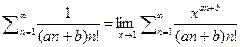 то дифференцируя получим
то дифференцируя получим 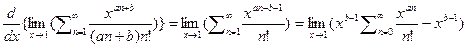 а значит
а значит
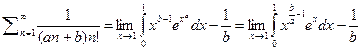 аналогично находим что
аналогично находим что
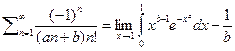 если же положить а=1 то искомые интегралы возьмутся по частям и тогда будем иметь:
если же положить а=1 то искомые интегралы возьмутся по частям и тогда будем иметь:
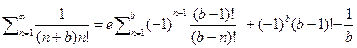 а также
а также
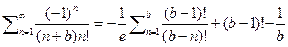
2) Ряд вида 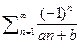 действуя также как и в случае (1) будем иметь
действуя также как и в случае (1) будем иметь 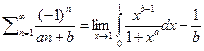 опять же для
опять же для 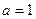
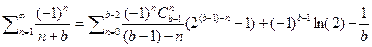

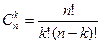
№2 Ряды сводящиеся к неэлементарным функциям
1) Рассмотрим ряд вида 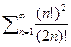 преобразуем его в следующему виду
преобразуем его в следующему виду
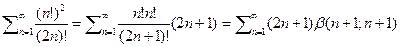 где
где 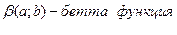
Рассмотрим интегральную форму бета функции 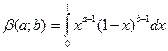 , а значит будем иметь
, а значит будем иметь 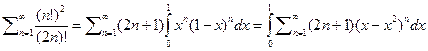 далее проведём замену
далее проведём замену
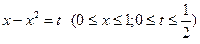 тогда, используя преобразование Эйлера, получим
тогда, используя преобразование Эйлера, получим 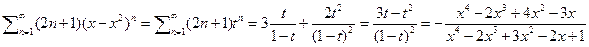
таким образом 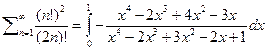 выделим целую часть и получим что
выделим целую часть и получим что  дале применим теорему Остроградского
дале применим теорему Остроградского 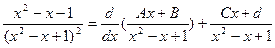 будем иметь
будем иметь
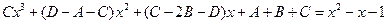 откуда
откуда 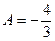 ;
; 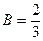 ;
; 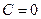 ;
; 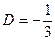 а значит
а значит  следовательно
следовательно
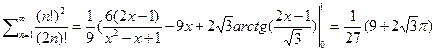 таким образом
таким образом
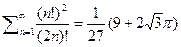
Дата добавления: 2015-12-21; просмотров: 35; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
