Числовые последовательности произвольного вида
№1 Суммирование с использованием первых разностей
1) Теперь приступим к нахождению сумм числовых последовательностей не образующих конечных разностей, но при этом уже заданных некоторой формулой.
2) Рассмотрим последовательность 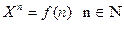 , где для
, где для 
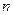 выполняется
выполняется 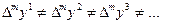 для нахождения её суммы можно воспользоваться следующим приёмом. Пусть
для нахождения её суммы можно воспользоваться следующим приёмом. Пусть 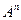 -частичная сумма тогда An+1-An=Xn. Если знаком∑ обозначить формулу n- ного элемента последовательности, разность которой Xn, то искомая сумма будет равна:
-частичная сумма тогда An+1-An=Xn. Если знаком∑ обозначить формулу n- ного элемента последовательности, разность которой Xn, то искомая сумма будет равна:
Sn= ∑ Xn+Xn+C (7)
2) a) Пусть Xn=1, тогда ∑ Xn=n;
б) Пусть Xn=n, тогда ∑ Xn= 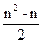 ; поскольку
; поскольку 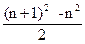 -
- 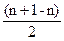 =n;
=n;
в) Пусть Xn=n2, тогда ∑ Xn= 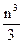 -
- 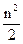 +
+ 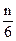 ; поскольку
; поскольку 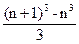 -
- 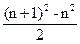 +
+ 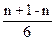 =
=
= 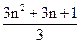 -n-
-n- 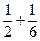 =n2;
=n2;
3) Рассмотрим ряд 1+9+25+49+…+(2n-1)2
а) Тогда Xn=4n2-4n+1
б) ∑ Xn= 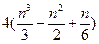 -
- 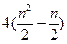 +n=
+n= 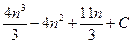
в) S n=  ; 1=
; 1= 

г) S n= 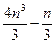
4) Поиск жепоследовательности ∑ Xn в сущности схож с операцией интегрирования и требует значительного интуитивного подхода, поэтому мы не будем уделять ему много времени и сразу перейдём к методу нахождения суммы последовательности который работает во всех случаях которые только могут встретится.
№2 Формула Эйлера-Маклорена
1) Далее будет выведена одна из важнейших формул теории числовых рядов впервые полученная Леонардом Эйлером и позволяющая решительно в любых случаях, находить суммы рядов с любой точностью. Начнём мы с получения ряда Тейлора в несколько необычном виде, в нём поменяются местами роль переменной и постоянной.
По определению дифференциала функции имеем 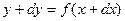 ,а так же
,а так же  и вообще
и вообще 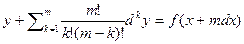 или
или
|
|
|
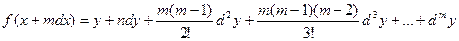 далее положим что
далее положим что  тогда будем иметь
тогда будем иметь 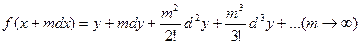 так как
так как 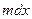 может быть конечно, то можно положить
может быть конечно, то можно положить 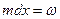 откуда
откуда 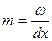 а значит
а значит  этот ряд по своей сути является рядом Тейлора
этот ряд по своей сути является рядом Тейлора
2) Рассмотрим последовательность в котором индексу 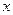 соответствует элемент
соответствует элемент 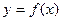 , тогда предшествующий элемент этой же последовательности
, тогда предшествующий элемент этой же последовательности 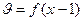 можно выразить через
можно выразить через 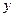 положив в ранее полученной формуле
положив в ранее полученной формуле 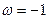 , а значит будем иметь:
, а значит будем иметь:
а) 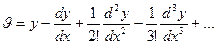
далее, просуммировав обе части равенства а) получим, что б) 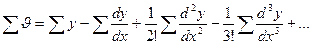
(Под символом 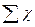 подразумевается сумма x членов последовательности вида
подразумевается сумма x членов последовательности вида 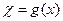 )
)
Также ясно, что в) 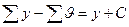 где постоянная
где постоянная 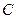 выбирается так, что бы при
выбирается так, что бы при 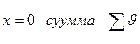 исчезала, а значит, объединяя формулы б) и в) получим:
исчезала, а значит, объединяя формулы б) и в) получим:
г) 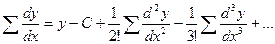
3) Теперь применим полученную формулу для нахождения суммы последовательности 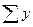 . Произведем в г) замену
. Произведем в г) замену 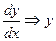 ;
; 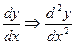 и.т.д.
и.т.д.
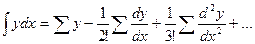
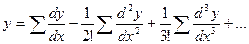

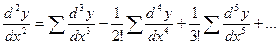
и.т.д.
Далее нетрудно заметить, что в первом равенстве справа стоит искомая сумма 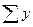 плюс суммы вида
плюс суммы вида 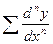 , которые встречаются во всех нижеследующих равенствах. Тогда законно предположить, что
, которые встречаются во всех нижеследующих равенствах. Тогда законно предположить, что 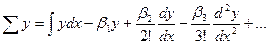 где
где  - некие числа подлежащие определению. Определить же эти числа можно подставляя найденные нами ранние выражения для
- некие числа подлежащие определению. Определить же эти числа можно подставляя найденные нами ранние выражения для 
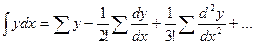 +
+
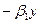
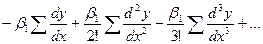 +
+
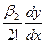


 и.т.д.
и.т.д.
откуда для определения  имеем следующие уравнения
имеем следующие уравнения
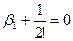
 и вообще
и вообще
|
|
|
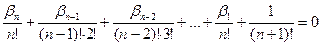 или
или 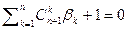
Эти числа впервые были получены и использованы великим математиком Бернулли и носят его имя. Далее будут приведены первые 22 числа Бернулли, все числа с нечётными номерами 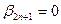 это их свойство, как будет показано далее, проистекает из того, что они появляются в разложении чётноё функции:
это их свойство, как будет показано далее, проистекает из того, что они появляются в разложении чётноё функции:
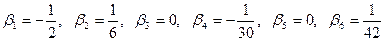
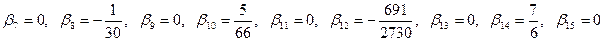
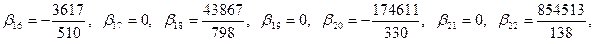
4) Окончательно получим:
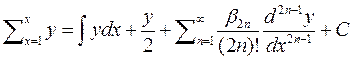 (8)
(8)
Формула (8) носит имя Эйлера-Маклорена.
5) Как видно данная формула даёт точное значение суммы последовательности, если общая формула 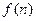 которой имеет конечное количество производных, если же данная функция имеет бесконечное количество производных то точное значение будет выражаться функциональным рядом, исследование этого случая будет проведено во второй половине работы.
которой имеет конечное количество производных, если же данная функция имеет бесконечное количество производных то точное значение будет выражаться функциональным рядом, исследование этого случая будет проведено во второй половине работы.
6) Как известно функция  имеет
имеет 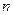 производных а значит можно найти общей вид суммы
производных а значит можно найти общей вид суммы 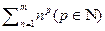 :
:
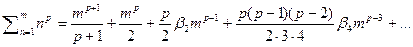
Ввиду частой встречаемости задач по нахождению таких сумм приведём формулы сумм степеней до 12 включительно:
0) 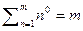 1)
1) 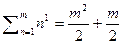 2)
2) 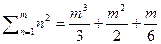 3)
3) 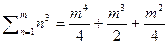
4) 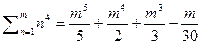 5)
5) 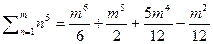
6) 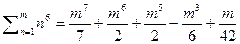 7)
7) 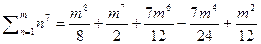
8) 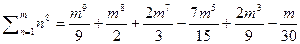
9) 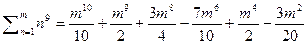
11) 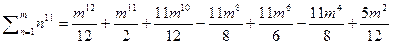
12) 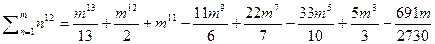
&2 Бесконечные суммы (ряды)
Дата добавления: 2015-12-21; просмотров: 19; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
