Простейшие ряды и их свойства
№1 Бесконечная сумма
1) Основным объектом рассмотрения второй части работы являются бесконечные суммы или ряды, как числовые, так и функциональныеБесконечнымрядом мы называем следующую сумму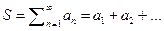 
, где 
произвольные действительные числа. Остатком ряда мы назовём величину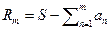 
понятно, что 
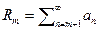а значит поскольку для 
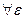выполняется 
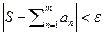лишь только 
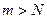, то и 
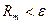отсюда и необходимый признак существования суммы S 
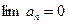Для рядов обладающих конечной суммой мы найдём соответствующие значения этих сумм. Но сначала отметим, что необходимый признак сходимости ряда ещё не является достаточным, поэтому кратко изложим основные достаточные признаки сходимости рядов.
№2 Достаточный признак сходимости рядов
1) Имеют место следующие признаки сходимости рядов:
Пусть помимо ряда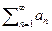 
дан сходящийся {расходящийся} ряд 
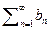тогда, если начиная с какого то N будет 
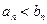то и 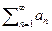будет сходится{расходится}. Предельный вариант этого признака:
Если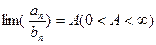 
, то ряд 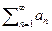сходится{расходится}, если сходится{расходится} ряд .
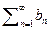Это следует из того, что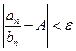 
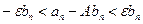à 
à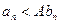 
{ 
}
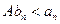2) Именные признаки сходимости:
а) Признак Каши (Основан на сравнении ряда с геометрической прогрессией)
Пусть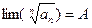 
, тогда, если 0<A<1 ряд сходится, если же A>1 ряд расходится.
б) Признак Даламбера
Пусть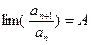 
, тогда, если 0<A<1 ряд сходится, если же A>1 ряд расходится.
в) Признак Раабе
Пусть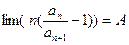 
тогда, если A<1 ряд сходится, если же A>1 ряд расходится.
№3 Простейшие ряды
1) Приступим к нахождению сумм простейших рядов для вычисления которых не требуются особые специальные приёмы, например возьмём ряд 
Найти сумму этого ряда можно просто разложив эту дробь на простые дроби, для этого воспользуемся тем, что коэффициенты в разложении на простые дроби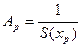 
где 
- простая дробь а 
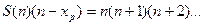откуда получим 
Из симметрии этого выражения можно сделать вывод о том что практически все члены данного ряда будут исчезать, а останутся только несколько начальных, и бесконечно малые конечные. Действительно написав первые пять строчек суммы прейдём к выводу что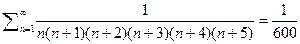 
|
|
|
№3 Функциональные ряды
1) Перейдём теперь к рассмотрению функциональных рядов. Поскольку многие числовые ряды могут быть приведены к функциональным рядам предельным переходом: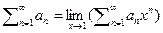 
мы большую часть работы посветим именно им. Функциональным рядом называют сумму вида 
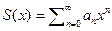. Также стоит упомянуть асимптотическим ряд вида 
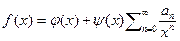В основном мы будем рассматривать равномерно сходящиеся ряды для которых при 
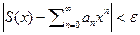для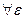
2) Над равномерно сходящимися рядами определены следующие операции:
а)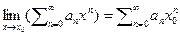 
б)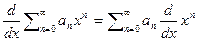 
в) 
3) Если дан числовой ряд 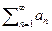, то 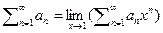лишь только предел справа существует.
4) Теперь с помощью указанных свойств найдём суммы рядов проистекающих из простейших. Рассмотрим ряд вида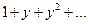 
вспоминая формулу суммы геометрической прогрессии находим что для 0<y<1 
|
|
|
5) Пожив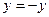 
получим, что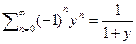 
6) Продифференцировав один раз обе части вышеуказанного равенства будем иметь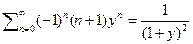 
далее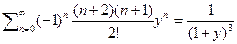 
и вообще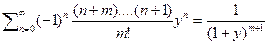 
и аналогично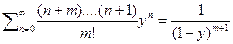 
7) Вспомним задачу из вступления, найти коэффициенты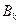 
в разложении по степеням
выражения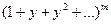 
И так будем иметь 
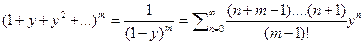то есть 
8) Снова возьмём ряд и умножим его на 
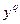и продифференцируемтогда будем иметь 
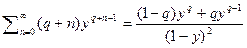откуда 
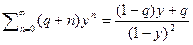сноваумножим его на 
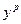тогда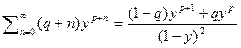 
далее будем иметь
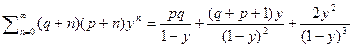
9) Рассмотрим геометрическую прогрессию с конечным числом членов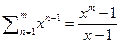 
умножим обе части равенства на 
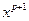получим 
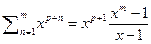далее продифференцируем равенство будем иметь: 
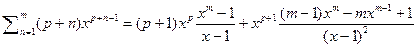деля обе части на 
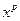получим:
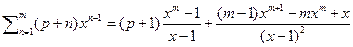
Дата добавления: 2015-12-21; просмотров: 24; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!