Основные формулы интегрирования. (табличные интегралы)
,
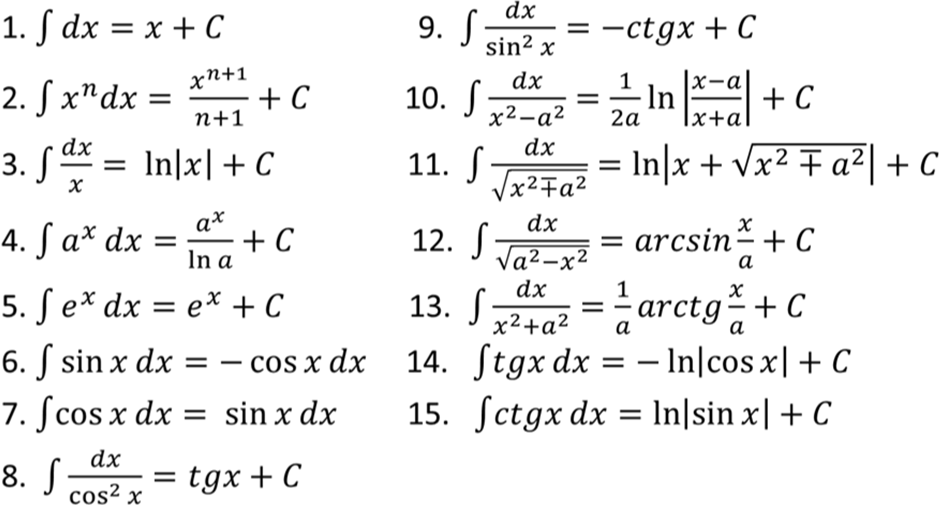
Примеры:
Найти следующие интегралы:
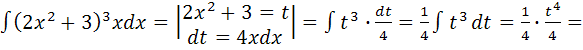
s New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:noProof/><w:sz w:val="32"/><w:sz-cs w:val="32"/><w:lang w:val="EN-US" w:fareast="RU"/></w:rPr><m:t>+C</m:t></m:r></m:e></m:nary></m:e><m:e/></m:eqArr></m:e></m:nary></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
Определенный интеграл.
Определенный интеграл вычисляется по формуле Ньютона –Ленйбница. С геометрической точки зрения – определенный интеграл равен площади криволинейной трапеции.
y=f(x)
|
|
|
X
0
Свойства определенного интеграла:
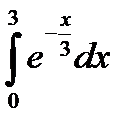Вычисление определенного интеграла. Формулу Ньютона-Лейбница. Пример:
Вычислить определенный интеграл:
Метод замены переменной в определенном интеграле.
Пример:
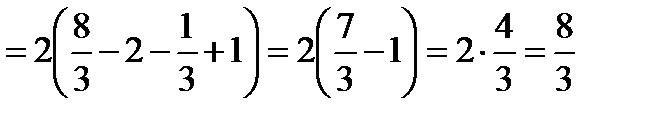
Приложения опредеделенного интеграла. Площадь плоской фигуры.
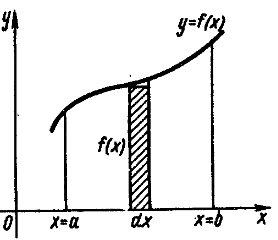Найдем площадь S криволинейной
трапеции, ограниченной кривой y =ƒ ( x ), осью Ox и двумя прямыми x = a и x = b, где a ≤ x ≤ b, ƒ ( x )≥0 , S – площадь прямоугольника с основанием dx и высотой ƒ ( x ), т.е. dS = ƒ ( x ) dx Интегрируя это равенство в пределаот a до b, получим
|
|
|
Если криволинейная трапеция ограниченная кривой y = ƒ( x ), осью
Ox и прямыми x = a и x = b , лежит под осью Ox, то
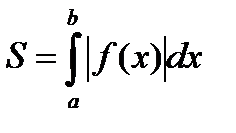
Если фигура, ограниченная кривой ƒ( y ), осью Ox и прямыми
x = a и x = b, расположена по обе стороны от оси Ox, то
Фигура S ограничена двумя пересекающимися кривыми
и и прямыми x = a и x = b, где a ≤ x ≤ b и
Площадь вычисляется по формуле
Примеры.
1. 
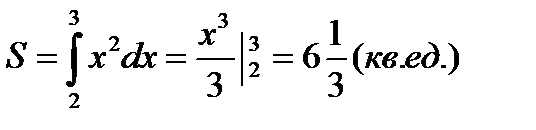Вычислить площадь криволинейной трапеции, ограниченной параболой и прямыми х=2 и х=3 и осью Ox . По формуле
Находим:
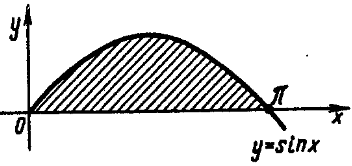
2. 
y=sinx, y=0 и
Искомая площадь ограничена полуволной синусоиды и осью Ох.
3. у=-6х, у=0 и х=4.
Фигура расположена под осью Ох. Следовательно, ее
площадь находим по формуле
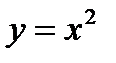
4. 
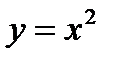и у=2х.
Данная фигура ограничена параболой и
прямой у=2х. Для определения точек пересечения заданных линий решим систему уравнений :
|
|
|
откуда находим
Используя для нахождения площади формулу
получим
5. 
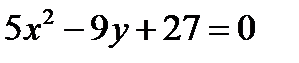
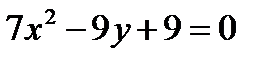Фигура, ограничена линиями и
Найдем точки пересечения данных парабол, выразим из каждого уравнения переменную у и решим систему уравнений:
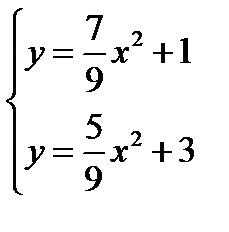
откуда
Так как фигура симметрична относительно оси Оу, то найдем
половину ее площади, взяв пределы интегрирования от 0 до 3, и
результат удвоим:
Комплексные числа.
Комплексными числами называются числа вида 
, где 
- действительные числа. Число 
, определяемое равенством 
, называется мнимой единицей.
Запись комплексного числа в виде 
называется алгебраической формой комплексного числа.
При 
комплексное число обращается в чисто мнимое число 
.
Комплексное число 
называется комплексно сопряженным с числом и обозначается 
.
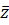Комплексные числа , и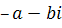 
, называются противоположными.
|
|
|
Модулем комплексного числа называется число 
Действия над комплексными числами, заданными в алгебраической форме:
Сложение: (a + bi) + (c + di) = (a + c) + (b + d)i.
Вычитание: (a + bi) − (c + di) = (a − c) + (b − d)i.
Умножение: 
Деление:
Дата добавления: 2020-12-22; просмотров: 254; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!