Приведение измеренных расстояний к центрам пунктов и редуцирование на плоскость проекции Гаусса-Крюгера
| Название пункта | DM (м) | h (м) | Н (м) | 
(м)
| 
(м)
| 
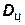(м)
| DГ (м) | 
(м)
| 
(м)
| 
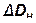(км)
| 
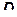(м)
| 
(м)
|
| Мокринский | 205,03 | |||||||||||
| 798,325 | -50,440 | 0,0738 | 798,399 | -1,5933 | 796,80 6 | -0,0225 | 796,78 2 | -88,748 | 0,0773 | 796,860 | ||
| пп1234 | 154,59 | |||||||||||
| 706,231 | -23,900 | -0,4044 | 705,827 | -0,0158 | 705,811 | -88,585 | 0,0681 | 705,879 | ||||
| пп718 | 130,69 | |||||||||||
| 548,978 | 18,880 | -0,3247 | 548,653 | -0,0121 | 548,641 | -88,537 | 0,0529 | 548,694 | ||||
| пп010 | 149,57 | |||||||||||
| 639,264 | 40,68 | 0,4421 | 639,706 | -1,2943 | 638,412 | -0,0170 | 638,395 | -88,545 | 0,0616 | 638,456 | ||
| Южный | 190,25 |
|
Вычисление координат точек хода полигонометрии |
| Таблица 23 | ||||||||||||||||||
| Назв. пункта | Изм.угол | Испр. угол | D (м) | Дир.угол | Приращения коорд.(м) | Координаты (м) | ||||||||||||||
| ° | ' | " | ° | ' | " | 
| 
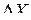
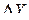
|  испр
|  испр
| X | Y | |||||||||
| Каменский |
| |||||||||||||||||||
| + | 0 | 0 | 1,4 | 190 | 50 | 47,9 |
| |||||||||||||
| Мокринский | 154 | 06 | 50,3 | 154 | 06 | 51,7 | + 0,034 | + 0,025 | 6323522,355 | 11411148,583
| ||||||||||
| + | 0 | 0 | 1,4 | 796,860 | 164 | 57 | 39,6 | -769,567 | +206,766 | -769,533 | +206,791 |
| ||||||||
| пп1234 | 185 | 11 | 44,7 | 185 | 11 | 46,1 | + 0,030 | + 0,022 | 6322752,822 | 11411355,374 | ||||||||||
| + | 0 | 0 | 1,4 | 705,879 | 170 | 09 | 25,7 | -695,489 | +120,667 | -695,459 | +120,689 |
| ||||||||
| пп718 | 192 | 20 | 48,8 | 192 | 20 | 50,2 | + 0,023 | + 0,017 | 6322057,363 | 11411476,063 | ||||||||||
| + | 0 | 0 | 1,4 | 548,694 | 182 | 30 | 16,0 | -548,170 | -23,976 | -548,147 | -23,959 |
| ||||||||
| пп010 | 176 | 47 | 07,9 | 176 | 47 | 09,3 | + 0,027 | + 0,020 | 6321509,216 | 11411452,104 | ||||||||||
| + | 0 | 0 | 1,4 | 638,457 | 179 | 17 | 25,3 | -638,408 | +7,907 | -638,381 | +7,927 |
| ||||||||
| Южный | 212 | 44 | 20,3 | 212 | 44 | 21,7 | 6320870,835 | 11411460,031 | ||||||||||||
| 212 | 01 | 47,0 |
| |||||||||||||||||
| Пролетарский |
| |||||||||||||||||||
| -2651,520 | +311,448 |
| ||||||||||||||||||
|
|
| |||||||||||||||||||
| ° | ' | " | Fx= | Fy= |
| |||||||||||||||
| доп. невязка | 0 | 22 | S D = | 2689,891 | -0,114 | -0,083 |
| |||||||||||||
| угл. невязка | - | 0 | 7 | Fs = | 0,141 | F отн.=1 | : 19 065 | F отн. доп. = | 1:10 000 | |||||||||||
Вывод: Угловая и относительная невязки хода соответствуют точности полигонометрии 1 разряда. Данные могут быть использованы для дальнейшего уравнивания сети.
На заключительном этапе предварительной обработки необходимо сделать вывод о качестве геодезических определений и вычертить схему сети.
Уравнивание геодезической сети параметрическим способом
Краткие сведения из алгоритма способа
Сущность параметрического способа отражается в принципах, положенных в основу составления уравнений поправок. Дальнейшая задача сводится к их решению при условии метода наименьших квадратов.
Для составления уравнений поправок выбирают независимые параметры 
. В качестве параметров выбирают величины, которые связаны функциональными зависимостями с результатами измерений. Для всех независимых параметров назначают их предварительные значения 
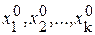. К ним из уравнивания отыскивают поправки 
.
|
|
|
Обозначим численные значения измеренных величин за 
, j = 1,.. , n, где n – количество измеренных величин и будем называть их уравниваемыми величинами. Уравненные значения этих величин обозначим за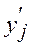 
. В качестве независимых параметров обычно принимают координаты пунктов.
Независимые параметры связаны функциональными зависимостями с уравниваемыми величинами
.
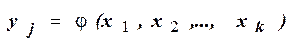Это выражение называется уравнением связи, оно справедливо и по отношению к уравненным величинам и уравненным параметрам
, (19)
причем 
, где 
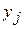- измеренное значение, 
- поправка к измеренной величине,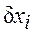 
- поправки к предварительным значениям параметров.
Систему уравнений (19) приводят к линейному виду и получают систему линейных уравнений поправок:
,
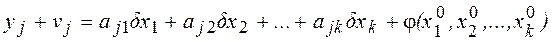или 
, (20)
где 
- свободный член уравнения поправок;
- коэффициенты уравнений поправок, вычисляемые по формулам:
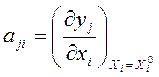. (21)
В матричной форме записи система параметрических уравнений имеет вид:
, (22)
|
|
|
где 
- вектор-столбец поправок в измеренные величины, количество строк которого (n) совпадает с количеством измеренных величин;
- матрица коэффициентов уравнений поправок, количество строк матрицы соответствует количеству измеренных величин(n), а столбцов – количеству параметров (k);
- вектор поправок к приближенным значениям параметров;
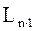- вектор свободных членов уравнений поправок.
Для приведения системы уравнений к равноточному виду и переходу к системе нормальных уравнений умножим систему (22) слева на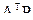 
, где 
- транспонированная матрица коэффициентов уравнений поправок; P– диагональная матрица весовых коэффициентов измеренных величин. Веса измеренных величин определяются по формуле 
, где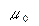 
- ошибка единицы веса, назначаемая до уравнивания, 
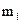- средняя квадратическая ошибка j измерения. Система нормальных уравнений имеет вид:
, (23)
где 
- матрица коэффициентов нормальных уравнений;
.
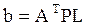Решение системы (23) находим в виде
, (24)
где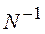 
- матрица, обратная к матрице нормальных уравнений.
Подставив решение системы нормальных уравнений в выражение (22), найдем вектор поправок в измеренные величины.
После этого необходимо произвести оценку точности. Вычисляют ошибку единицы веса после уравнивания по формуле :
, (25)
где n –число всех измерений,
k – число параметров;
VT – транспонированный вектор поправок в измеренные величины;
Р – матрица весов измеренных величин;
V - вектор поправок в измеренные величины.
Точность определения параметров из уравнивания характеризуется величиной средней квадратической ошибки, значение которой определяется из соотношения 
, где Q–обратные веса параметров, являющиеся диагональными элементами матрицы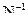 
.
Дата добавления: 2020-11-23; просмотров: 120; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!