Практическое занятие № 3. «Применение Eviews при построении и анализе линейной однофакторной модели регрессии» (Выполняется самостоятельно).
Пример 3. Компания American Express Company в течение долгого времени полагала, что владельцы ее кредитных карточек имеют тенденцию путешествовать более интенсивно, как по делам бизнеса, так и для развлечений. Как часть объемного исследования, проведенного Нью-Йоркской компанией рыночных исследований по заказу American Express Company, было осуществлено определение взаимосвязи между путешествиями и расходами владельцев кредитных карточек. Исследовательская фирма случайным образом выбрала 25 владельцев карточек из компьютерного файла American Express Company и записала суммы их общих расходов за определенный период времени. Для выбранных владельцев карточек фирма так же подготовила и разослала по почте вопросы о числе миль, которые провел в путешествиях владелец карточки за изучаемый период. Данные, полученные из опроса, составляют исходную информацию анализа (Х – число миль, проведенных в пути; У – расходы путешественников (усл. ден ед.).
| № п\п | Miles (Х) | Costs (У) |
| 1 | 1211 | 1802 |
| 2 | 1345 | 2405 |
| 3 | 1422 | 2005 |
| 4 | 1687 | 2511 |
| 5 | 1849 | 2332 |
| 6 | 2026 | 2305 |
| 7 | 2133 | 3016 |
| 8 | 2253 | 3385 |
| 9 | 2400 | 3090 |
| 10 | 2468 | 3694 |
| 11 | 2699 | 3371 |
| 12 | 2806 | 3998 |
| 13 | 3082 | 3555 |
| 14 | 3209 | 4692 |
| 15 | 3466 | 4244 |
| 16 | 3643 | 5298 |
| 17 | 3852 | 4801 |
| 18 | 4033 | 5147 |
| 19 | 4267 | 5738 |
| 20 | 4498 | 6420 |
| 21 | 4533 | 6059 |
| 22 | 4804 | 6426 |
| 23 | 5090 | 6321 |
| 24 | 5233 | 7026 |
| 25 | 5439 | 6964 |
1. Создать файл с исходными данными в среде Excel (файл example _03. xls).
|
|
|
2. Осуществить импорт исходных данных в Eviews.
3. Создать рабочий файл (workfile).
4. Найти значения описательных статистик по каждой переменной и объяснить их (рис. 51).
5. Построить поле корреляции моделируемого (результативного) и факторного признаков (рис. 52). Объяснить полученные результаты.
6. Найти значение линейного коэффициента корреляции и пояснить его смысл (рис. 53).
7. Определить параметры уравнения парной регрессии и интерпретировать их. Объяснить смысл полученного уравнения регрессии (рис. 54).
8. Оценить статистическую значимость коэффициента регрессии 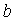 и уравнения в целом. Сделать выводы.
и уравнения в целом. Сделать выводы.
9. Объяснить полученное значение 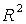 .
.
10. Построить эмпирическую и теоретическую линию регрессии и объяснить их (рис. 55).
11. Построить и проанализировать график остатков (рис. 56).
12. С вероятностью 0,95 построить доверительный интервал для оценки ожидаемого значения средних расходов владельцев карточек, дальность путешествий которых составила 4000 миль (рис. 57).
13. Оформить отчет по занятию.
Результаты расчетов по практическому занятию №3 для самоконтроля:
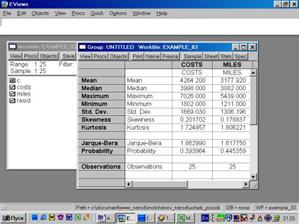
Рис. 51.
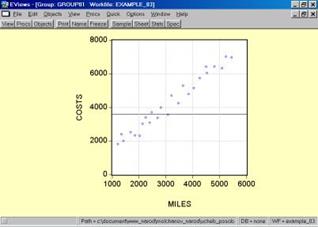
Рис. 52.
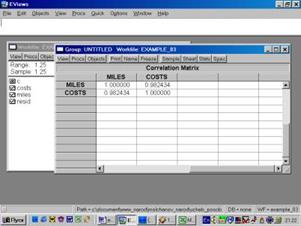
Рис. 53.
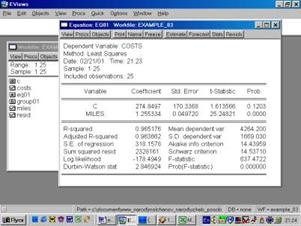
Рис. 54.
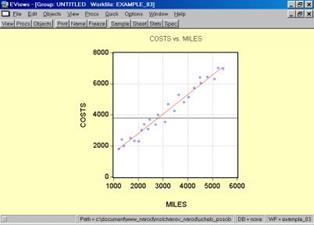
Рис. 55.
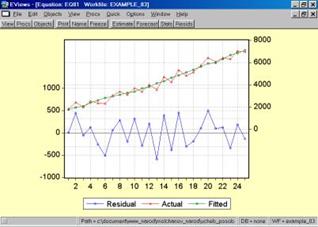
Рис. 56.
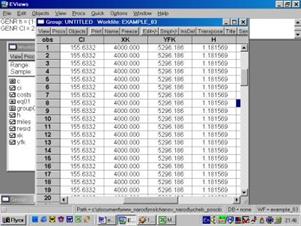
Рис. 57.
Лекция 3.
|
|
|
Ошибки измерения факторов и фиктивные переменные
6.1. Ошибки измерения факторов
Пусть теперь нарушается гипотеза 2, и независимые факторы наблюдаются с ошибками (здесь используются обозначения первых двух форм уравнения регрессии):
z = z0 + e, или в разрезе наблюдений: Z = Z0 + e,
где z0 и e - n-вектора-строки истинных значений факторов и ошибок их измерений;
Z0 и e - соответствующие N ´ n-матрицы значений этих величин по наблюдениям.
Предполагается, что истинные значения и ошибки независимы друг от друга (по крайней мере, не скоррелированы друг с другом) и известны их матрицы ковариации (одинаковые для всех наблюдений):
E(z0/, e ) = 0, E(z0/,z0) = M0, E( e / e ) = W.
Уравнение регрессии можно записать в следующей форме:
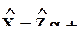 e - e a,
e - e a,
(т.е. остатки теперь не могут быть независимыми от факторов-регрессоров) и в рамках сделанных предположений доказать, что
E(M) = M0 + W, E(a) = (M0 + W )-1M0 a,
т.е. МНК-оценки теряют в такой ситуации даже свойство несмещенности. Как правило, они преуменьшены по сравнению с истинными значениями (в случае n = 1, 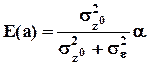 ).
).
Существуют три подхода к оценке параметров регрессии в случае наличия ошибок измерения независимых факторов.
|
|
|
а) Простая регрессия. Если имеется оценка W ковариационной матрицы ошибок W и ошибки регрессоров взаимно независимы с изучаемой переменной, то можно использовать следующий оператор оценивания:
a = (M-W)-1m,
который обеспечивает несмещенность оценок.
б) Инструментальные переменные. Если имеется n факторов y, которые взаимно независимы как с ошибками уравнения e, так и ошибками основных факторов e, то оценка
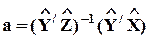
несмещена.
Исторически первой в этом классе получена оценка Вальда для случая n = 1. Для получения этой оценки i-я компонента вектора-столбца Y принимается равной единице, если zi больше своей медианы, и минус единице, если - меньше медианы (при нечетном N среднее значение теряется). В результате получается, что 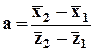
где 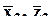 - средние значения переменных по верхней части выборки,
- средние значения переменных по верхней части выборки,
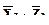 - их средние значения по нижней части выборки.
- их средние значения по нижней части выборки.
Такая оценка более эффективна, если исключить примерно треть “средних” наблюдений.
Позже эта оценка была обобщена: матрицу значений инструментальных переменных было предложено формировать столбцами рангов по наблюдениям соответствующих переменных z.
в) Ортогональная регрессия. Если ошибки факторов не зависят друг от друга и от ошибок в уравнениях (которые в этом случае интерпетируются как ошибки изучаемой переменной), их дисперсии одинаковы и равны дисперсии ошибки изучаемой переменной, а между истинными значениями переменных имеется линейная зависимость, то можно использовать ортогональную регрессию. Возвращаясь к обозначениям 3-го раздела,
|
|
|
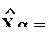 e и
e и
(M - l In)a = 0, a/a = 1.
В этом случае матрица ковариации ошибкок переменных имеет вид s 2 In. Если матрица ковариации ошибок есть s 2 W, то применяется регрессия в метрике W -1:
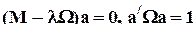 .
.
Для доказательства проводится преобразование в пространстве переменных с помощью матрицы C, такой, что 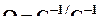 , после которого матрица ковариации ошибок переменных приобретает вид s 2 In, и становится возможным применить обычную ортогональную регрессию.
, после которого матрица ковариации ошибок переменных приобретает вид s 2 In, и становится возможным применить обычную ортогональную регрессию.
Ортогональная регрессия при принятых гипотезах приводит к состоятельным оценкам параметров.
6.2. Фиктивные переменные
С помощью фиктивных или псевдо- переменных, принимающих дискретные, обычно, целые значения, в регрессию включают качественные факторы.
Уточнение обозначений:
Z - N ´ n-матрица наблюдений за “обычными” независимыми факторами;
a - n-вектор-столбец параметров регрессии при этих факторах;
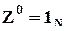 ;
;
b0 = b.
В этих обозначениях уравнение регрессии записывается следующим образом:
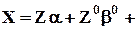 e.
e.
Пусть имеется один качественный фактор, принимающий два значения (например: “мужчина” и “женщина”, если речь идет о модели некоторой характеристики отдельных людей, или “годы войны” и “годы мира” - в модели, построенной на временных рядах наблюдений, которые охватывают периоды войны и мира, и т.д.). Ставится вопрос о том, влияет ли этот фактор на значение свободного члена регрессии.
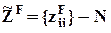 ´ 2-матрица наблюдений за качественным фактором (матрица фиктивных переменных):
´ 2-матрица наблюдений за качественным фактором (матрица фиктивных переменных): 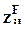 равен единице, если фактор в i-м наблюдении принимает 1-е значение, и нулю в противном случае;
равен единице, если фактор в i-м наблюдении принимает 1-е значение, и нулю в противном случае; 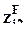 равен единице, если фактор в i-м наблюдении принимает 2-е значение, и нулю в противном случае.
равен единице, если фактор в i-м наблюдении принимает 2-е значение, и нулю в противном случае.
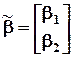 - 2-х компонентный вектор-столбец параметров при фиктивных переменных.
- 2-х компонентный вектор-столбец параметров при фиктивных переменных.
Исходная форма регрессии с фиктивными переменными:
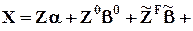 e.
e.
Поскольку сумма столбцов матрицы 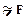 равна Z0, оценка параметоров непосредственно по этому уравнению невозможна.
равна Z0, оценка параметоров непосредственно по этому уравнению невозможна.
Проводится преобразование фиктивных переменных одним из двух спасобов.
а) В исходной форме регрессии исключается один из столбцов матрицы фиктивных переменных, в данном случае - первый.
 - матрица фиктивных переменных без первого столбца;
- матрица фиктивных переменных без первого столбца;
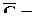 =
= 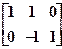 .
.
Тогда эквивалентная исходной запись уравнения имеет вид:
 + e,
+ e,
и после умножения матрицы 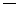 справа на вектор параметров получается запись уравнения регресии в которой отсутствует линейная зависимость между факторами-регрессорами:
справа на вектор параметров получается запись уравнения регресии в которой отсутствует линейная зависимость между факторами-регрессорами:
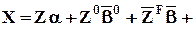 e,
e,
где 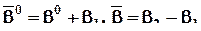 .
.
После оценки этих параметров можно определить значения исходных параметров b 0 и 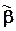 , предполагая, что сумма параметров при фиктивных переменных (в данном случае b 1 + b 2) равна нулю, т.е. влияние качественного фактора приводит к колебаниям вокруг общего уровня свободного члена:
, предполагая, что сумма параметров при фиктивных переменных (в данном случае b 1 + b 2) равна нулю, т.е. влияние качественного фактора приводит к колебаниям вокруг общего уровня свободного члена:
 .
.
б) Предполагая, что сумма параметров при фиктивных переменных равна нулю, в исходной форме регрессии исключается один из этих параметров, в данном случае - первый.
b - вектор-стобец параметров при фиктивных переменных без первого элемента;
C 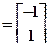 .
.
Эквивалентная исходной запись уравнения принимает форму:
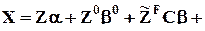 e,
e,
и после умножения матрицы C слева на матрицу наблюдений за фиктивными переменными получается запись уравнения регрессии, в которой также отсутствует линейная зависимость между регрессорами:
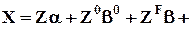 e.
e.
После оценки параметров этого уравнения недостающаяся оценка параметра b 1 определяется из условия b 1 = - b 2.
Качественный фактор может принимать больше двух значений. Так, в классической модели выделения сезонных колебаний он принимает 4 значения в случае поквартальных наблюдений и 12 значений, если наблюдения проводились по месяцам. Матрица 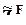 в этой модели имеет размерность, соответственно, N ´ 4 или N ´ 12.
в этой модели имеет размерность, соответственно, N ´ 4 или N ´ 12.
Пусть в общем случае качественный фактор принимает k значений. Тогда:
матрица 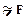 имеет размерность N ´ k, вектор-столбец
имеет размерность N ´ k, вектор-столбец 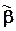 - размерность k, матрицы
- размерность k, матрицы  и ZF - N ´ (k - 1), вектора-столбцы
и ZF - N ´ (k - 1), вектора-столбцы 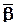 и b - k - 1;
и b - k - 1;
k ´ (k+1) матрица 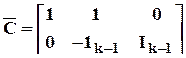 , k ´ (k - 1) матрица
, k ´ (k - 1) матрица 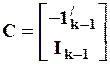 ;
; 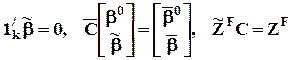 .
.
Можно показать, что
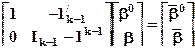 , или
, или 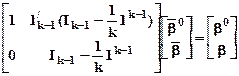 ,
,
где 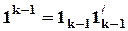 - (k - 1) ´ (k - 1)-матрица, состоящая из единиц; и далее показать, что результаты оценки параметров уравнения с фиктивными переменными при использовании обоих указанных подходов к устранению линейной зависимости факторов-регрессоров одинаковы.
- (k - 1) ´ (k - 1)-матрица, состоящая из единиц; и далее показать, что результаты оценки параметров уравнения с фиктивными переменными при использовании обоих указанных подходов к устранению линейной зависимости факторов-регрессоров одинаковы.
После оценки регрессии можно применить t-критерий для проверки значимости влияния качественного фактора на свободный член уравнения.
Если k слишком велико и приближается к N, то на параметры при фиктивных переменных накладываются более жесткие ограничения (чем равенство нулю их суммы). Так, например, если наблюдения проведены в последовательные моменты времени, и вводится качественный фактор “время”, принимающий особое значение в каждый момент времени, то 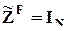 , и обычно предполагается, что значение параметра в каждый момент времени (при фиктивной переменной каждого момента времени) больше, чем в предыдущий момент времени на одну и ту же величину. Тогда роль матрицы C играет N-вектор-столбец T, состоящий из чисел натурального ряда, начиная с 1, и
, и обычно предполагается, что значение параметра в каждый момент времени (при фиктивной переменной каждого момента времени) больше, чем в предыдущий момент времени на одну и ту же величину. Тогда роль матрицы C играет N-вектор-столбец T, состоящий из чисел натурального ряда, начиная с 1, и 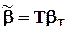 , где b T - скаляр. Уравнение регрессии с фактором времени имеет вид (эквивалентная исходной форма уравнения при использовании способа “б” исключения линейной зависимости фиктивных переменных):
, где b T - скаляр. Уравнение регрессии с фактором времени имеет вид (эквивалентная исходной форма уравнения при использовании способа “б” исключения линейной зависимости фиктивных переменных):
 e.
e.
Метод фиктивных переменных можно использовать для проверки влияния качественного фактора на коэффициент регрессии при любом обычном факторе. Исходная форма уравнения, в которое вводится качественный фактор для параметра a j, имеет следующий вид:
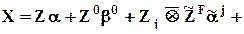 e,
e,
где 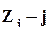 -й столбец матрицы Z,
-й столбец матрицы Z,
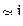 - k-вектор-столбец параметров влияния качественного фактора на a j;
- k-вектор-столбец параметров влияния качественного фактора на a j;
в векторе a j-я компонента теперь обозначается 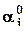 - средний уровень параметра a j;
- средний уровень параметра a j;
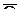 - операция прямого произведения столбцов матриц.
- операция прямого произведения столбцов матриц.
Замечание
Прямое произведение матриц A Ä B, имеющих размерность, соответственно, mA ´ nA и mB ´ nB есть матрица размерности (mAmB) ´ (nAnB) следующей структуры:
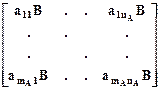
Прямое произведение матриц обладает следующими свойствами:
(A Ä B)(C Ä D) = (AC) Ä (BD), если произведения AC и BD имеют смысл,
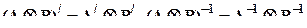 .
.
Прямое произведение столбцов матриц применимо к матрицам, имеющим одинаковое число строк, и осуществляется путем проведения операции прямого произведения последовательно с векторами-строками матриц.
Приоритет прямого произведения матриц выше, чем обычного матричного произведения.
При использовании способа “а” эквивалентная исходной форма уравнения имеет вид (форма “а”):
 e,
e,
где 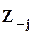 - матрица Z без j-го столбца,
- матрица Z без j-го столбца,
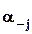 - вектр a без j-го элемента;
- вектр a без j-го элемента;
а в случае применения способа “б” (форма “б”):
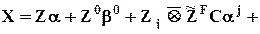 e.
e.
Все приведенные выше структуры матриц и соотношения между матрицами и векторами сохраняются.
В уравнение регрессии можно включать более одного качественного фактора. В случае двух факторов, принимающих, соответственно, k1 и k2 значения, форма “б” уравнения записывается следующим образом:
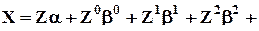 e,
e,
где вместо “F” в качестве индекса качественного фактора используется его номер.
Это уравнение может включать фиктивные переменные совместного влияния качественных факторов (взаимодействия фактров). В исходной форме компонента совместного влияния записывается следующим образом:
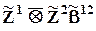 ,
,
где 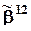 - k1 ´ k2-вектор-столбец
- k1 ´ k2-вектор-столбец 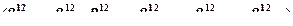 /,
/,
а 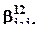 - параметр при фиктивной переменной, которая равна 1, если 1-й фактор принимает i1-е значение, а 2-й фактор - i2-е значение, и равна 0 в остальных случаях (вектором-столбцом наблюдений за этой переменной является (k1(i1-1)+i2)-й столбец матрицы
- параметр при фиктивной переменной, которая равна 1, если 1-й фактор принимает i1-е значение, а 2-й фактор - i2-е значение, и равна 0 в остальных случаях (вектором-столбцом наблюдений за этой переменной является (k1(i1-1)+i2)-й столбец матрицы 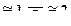 ).
).
Как и прежде, вектор параметров, из которого исключены все компоненты, линейно выражаемые через остальные, обозначается 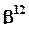 . Он имеет размерность (k1 - 1) ´ (k2 - 1) и связан с исходным вектором параметров таким образом:
. Он имеет размерность (k1 - 1) ´ (k2 - 1) и связан с исходным вектором параметров таким образом:
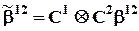 ,
,
где C1 и C2 - матрицы размерности k1 ´ (k1-1) и k2 ´ (k2-1), имеющие описанную выше структуру (матрица C).
Теперь компоненту совместного влияния можно записать следующим образом:
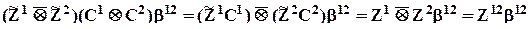 ,
,
а уравнение, включающее эту компоненту (форма “б”) -
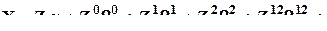 e.
e.
В общем случае имеется L качественных факторов, j-й фактор принимает kj значений. Пусть упорядоченное множество {1,2,...,L} обозначается F, а J - его подмножества. Общее их количество, включая пустое подмножество, равно 2L. Каждому такому подмножеству взаимно однозначно соответствует число, например, в системе исчисления с основанием 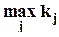 , и их можно упорядочить по возрастанию этих чисел. Если пустое подмножество обозначить 0, то можно записать J = 0,1,...,L,{1,2},...,{1,L},{2,3},...,{1,2,3},...,F. Тогда уравнение регрессии записывается следующим образом:
, и их можно упорядочить по возрастанию этих чисел. Если пустое подмножество обозначить 0, то можно записать J = 0,1,...,L,{1,2},...,{1,L},{2,3},...,{1,2,3},...,F. Тогда уравнение регрессии записывается следующим образом:
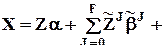 e
e 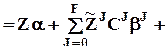 e
e 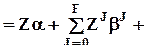 e,
e,
где 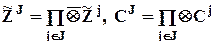 при j > 0; C0 = 1. Выражение
при j > 0; C0 = 1. Выражение 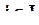 означает, что j принимает значения последовательно с 1-го по последний элемент подмножества J.
означает, что j принимает значения последовательно с 1-го по последний элемент подмножества J.
Очевидно, что приведенная выше запись уравнения для L = 2 является частным случаем данной записи.
Если p(J) - количество элементов в подмножестве J, то
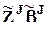 или
или 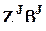 - J-е эффекты, эффекты p(J)-го порядка, при p(J) = 1 - главные эффекты, при p(J) > 1 - эффекты взаимодействия, эффекты совместного влияния или совместные эффекты.
- J-е эффекты, эффекты p(J)-го порядка, при p(J) = 1 - главные эффекты, при p(J) > 1 - эффекты взаимодействия, эффекты совместного влияния или совместные эффекты.
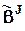 или b J - параметры соответствующих J-х эффектов или также сами эти эффекты.
или b J - параметры соответствующих J-х эффектов или также сами эти эффекты.
6.3. Дисперсионный анализ
Рассматривается частный случай уравнения регрессии с фиктивными переменными, когда оно включает только такие (фиктивные) переменные, и для каждого сочетания значений факторов имеется одно и только одно наблюдение за изучаемой переменной. Тогда 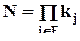 и уравнение имеет вид:
и уравнение имеет вид:
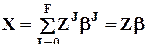 ,
,
в котором отсутствует вектор ошибок e, т.к. при учете эффектов всех порядков их сумма в точности равняется X.
Матрица Z имеет размерность N ´ N и она не вырождена. Поэтому b = Z - 1 X. Но чтобы получить общие результаты, имеющие значение и для частных моделей, в которых эффекты высоких порядков принимаются за случайную ошибку, ниже используется техника регрессионного анализа.
Это - регрессионная модель полного (учитываются эффекты всех порядков) одномерного (изучаемая переменная единственна) многофакторного дисперсионного анализа без повторений (для каждого сочетания значений фактров есть одно наблюдение).
Обычному линейному индексу 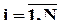 компонент вектора X можно поставить в соответствие мультииндекс I, принимающий значения из множества
компонент вектора X можно поставить в соответствие мультииндекс I, принимающий значения из множества 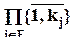 , так что, если I = {i1,i2,...,iL}, то
, так что, если I = {i1,i2,...,iL}, то 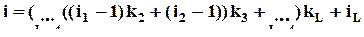 , и - при этом - обозначения xi и xI эквивалентны. При таком соответствии обычного индекса и мультииндекса в линейной последовательности значений мультииндекса быстрее меняются его младшие компоненты (с большим порядковым номером).
, и - при этом - обозначения xi и xI эквивалентны. При таком соответствии обычного индекса и мультииндекса в линейной последовательности значений мультииндекса быстрее меняются его младшие компоненты (с большим порядковым номером).
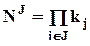 , если j > 0, и N0 = 1 - количество столбцов в матрице
, если j > 0, и N0 = 1 - количество столбцов в матрице 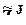 ;
;
 , если j > 0, и
, если j > 0, и 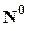 = 1 - количество столбцов в матрице
= 1 - количество столбцов в матрице 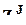 ; очевидно, что
; очевидно, что 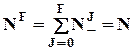 ;
;
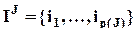 - мультииндекс с множеством значений
- мультииндекс с множеством значений 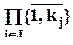 ; I = IF.
; I = IF.
Mb = m - система нормальных уравнений,
где M - N ´ N-матрица, b и m - N-вектора-столбцы и, как обычно, 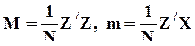 .
.
При выбранном порядке следования значений факторов от наблюдения к наблюдению (быстее меняют свои значения более младшие факторы)
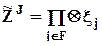 где x j есть
где x j есть 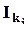 , если
, если 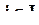 , или
, или 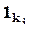 , в противном случае. Тогда
, в противном случае. Тогда
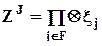 где x j есть
где x j есть 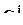 , если
, если 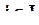 , или
, или 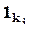 , в противном случае, и далее
, в противном случае, и далее
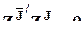 , если
, если 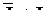 , т.е. переменные разных эффектов ортогональны друг другу,
, т.е. переменные разных эффектов ортогональны друг другу,
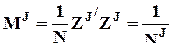
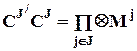 , M0 = 1;
, M0 = 1;
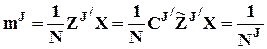
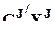 ,
,
где 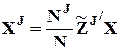 - NJ-вектор-столбец средних по сочетаниям значений факторов J с мультииндексом компонент IJ (
- NJ-вектор-столбец средних по сочетаниям значений факторов J с мультииндексом компонент IJ ( 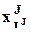 является средним значением x по тем наблюдениям, в которых 1-й фактор из множества J принимает i1-е значение, 2-й - i2-е значение и т.д.);
является средним значением x по тем наблюдениям, в которых 1-й фактор из множества J принимает i1-е значение, 2-й - i2-е значение и т.д.); 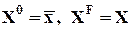 .
.
M - блочно-диагональная матрица {MJ}, m - вектор-столбец {mJ}.
После решения системы нормальных уравнений и перехода к “полным” векторам параметров эффектов получается следующее:
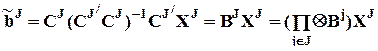 ,
,
где 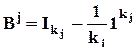 (как и прежде,
(как и прежде, 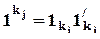 ), B0 = 1.
), B0 = 1.
Параметры разных эффектов 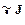 (разных по J) не зависят друг от друга, и исключение из уравнения некоторых из них не повлияет на значения параметров оставшихся эффектов.
(разных по J) не зависят друг от друга, и исключение из уравнения некоторых из них не повлияет на значения параметров оставшихся эффектов.
Чтобы получить более “прозрачные” формулы для определения парметров эффектов, следует ввести понятие сопоставимых векторов этих параметров.
Если  , то
, то
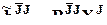 - NJ-вектор-столбец параметров
- NJ-вектор-столбец параметров  -го эффекта, сопоставимый с вектором
-го эффекта, сопоставимый с вектором 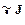 : он имеет ту же размерность, что и
: он имеет ту же размерность, что и 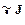 , и каждая компонента вектора
, и каждая компонента вектора 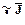 повторена в нем
повторена в нем 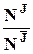 раз - так, что любой компоненте
раз - так, что любой компоненте 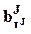 вектора
вектора 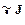 в векторе
в векторе 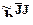 соответствует компонента
соответствует компонента 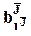 , для которой
, для которой 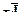 является подмножеством тех же элементов
является подмножеством тех же элементов 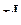 , что и
, что и  по отношению к J.
по отношению к J.
В этом выражении для сопоставимых векторов параметров эффектов
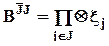 , где x j равен
, где x j равен 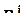 , если
, если 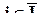 , или
, или 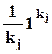 , в противном случае (
, в противном случае ( 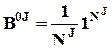 ,
, 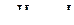 ).
).
Эти матрицы обладают следующим свойством: 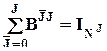 , откуда получается выражение
, откуда получается выражение
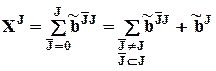
для рекурентного расчета параметров эффектов (например, если известны 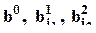 , то
, то 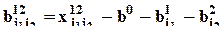 ).
).
При J = F это выражение представляет собой другую форму записи основного уравнения регрессии:
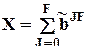 , т.е.
, т.е. 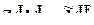 .
.
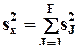 - основное тождество дисперсионного анализа, показывающее распределение общей дисперсии изучаемой величины по факторам и их взаимодействиям,
- основное тождество дисперсионного анализа, показывающее распределение общей дисперсии изучаемой величины по факторам и их взаимодействиям,
где 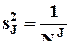
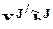 - дисперсия, объясненная совместным влиянием факторов J; представляет собой сумму квадратов с
- дисперсия, объясненная совместным влиянием факторов J; представляет собой сумму квадратов с 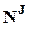 степенями свободы.
степенями свободы.
Все эти дисперсии не зависят друг от друга. Если совместное влияние факторов  так же существенно (или не существенно) как и факторов J, то статистика
так же существенно (или не существенно) как и факторов J, то статистика
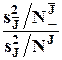 (предполагается, что она больше единицы)
(предполагается, что она больше единицы)
имеет 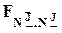 -распределение (предполагается, что x нормально распределено). Этот факт можно использовать для проверки гипотез о сравнительной существенности факторов и их взаимодействий.
-распределение (предполагается, что x нормально распределено). Этот факт можно использовать для проверки гипотез о сравнительной существенности факторов и их взаимодействий.
Обычно эффекты высоких порядков отождествляют со случайной ошибкой. Уравнение регрессии приобретает свою обычную форму и можно воспользоваться t- и F-критериями для проверки значимости отдельных факторов и их взаимодействий. Важно, что оценки оставшихся в уравнении эффектов при этом не меняются.
Переходя к более общему и более сложному случаю модели дисперсионного анализа с повторениями, полезно вспомнить следующее. Если в модели регрессионного анализа
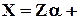 e
e
несколько строк матрицы Z одинаковы, то можно перейти к сокращенной модели, в которой из всех этих строк оставлена одна, а в качестве соответствующей компоненты вектора X взято среднее по этим наблюдениям с одинаковыми значениями независимых факторов. Т.е. совокупность наблюдений с одинаковыми значениями независимых факторов заменяется одним групповым наблюдением. При исходной гипотезе E( 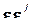 ) = s 2 I дисперсия остатка по этому наблюдению равна ng s 2, где ng - количество замененных наблюдений, и значения переменных в групповом наблюдении должны быть умножены на
) = s 2 I дисперсия остатка по этому наблюдению равна ng s 2, где ng - количество замененных наблюдений, и значения переменных в групповом наблюдении должны быть умножены на 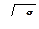 (в соответствии с ОМНК). Значения оценок параметров по исходной и сокращенной модели будут одинаковыми, но полная (
(в соответствии с ОМНК). Значения оценок параметров по исходной и сокращенной модели будут одинаковыми, но полная (  ) и остаточная (e/e) суммы квадратов в исходной модели будут больше, чем в сокращенной на сумму квадратов отклонений переменных x по исключенным наблюдениям от своей средней.
) и остаточная (e/e) суммы квадратов в исходной модели будут больше, чем в сокращенной на сумму квадратов отклонений переменных x по исключенным наблюдениям от своей средней.
Пусть теперь рассматривается регрессионная модель одномерного однофакторного дисперсионного анализа с повторениями:
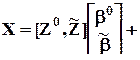 e.
e.
Фактор принимает k значений, и для каждого i-го значения существует ni наблюдений (ni повторений), т.е. исходная совокупность X разбита по какому-то признаку на k групп, причем сначала в ней идут наблюдения по 1-й группе, потом - по 2-й и т.д..
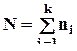 ;
; 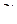 - N ´ k-матрица структуры
- N ´ k-матрица структуры  .
.
Всем повторениям в матрице Z соответствуют одинаковые строки, поэтому можно перейти к сокращенной модели.
 - среднее и
- среднее и 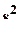 - дисперсия по i-й группе;
- дисперсия по i-й группе; 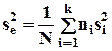 - суммарная дисперсия по группам. Сокращенная модель имеет следующий вид:
- суммарная дисперсия по группам. Сокращенная модель имеет следующий вид:
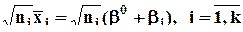 .
.
При естественном требовании 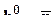 , которое эквивалентно
, которое эквивалентно  = 0, матрица C имеет вид
= 0, матрица C имеет вид  и
и  .
.
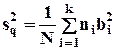 - объясненная дисперсия, равная полной дисперсии в сокращенной модели.
- объясненная дисперсия, равная полной дисперсии в сокращенной модели.
Полная дисперсия в исходной модели распадается на две части:
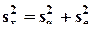
- объясненную и остаточную, или в терминах дисперсионного анализа - межгрупповую и внутригрупповую дисперсии, которые имеют, соответственно, k и N - k - 1 степеней свободы. Применяя F-критерий, можно оценить статистическую значимость использования данной группировки в целом или выделения отдельных групп.
Теперь рассматривается общий случай L-факторной модели.
В этом случае N больше NF на общее число повторений по всем сочетаниям значений факторов. Пусть
nI - число наблюдений при I-м сочетании значений факторов;  ;
;
xI - среднее значение и 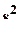 - дисперсия наблюдений при I-м сочетании;
- дисперсия наблюдений при I-м сочетании;
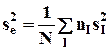 - суммарная внутригрупповая или остаточная дисперсия для исходной модели с N-NF-1 степенями свободы.
- суммарная внутригрупповая или остаточная дисперсия для исходной модели с N-NF-1 степенями свободы. 
Сокращенная модель имеет вид:
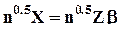 ,
,
где n - диагональная NF-матрица {nI};
X - NF-вектор-столбец {xI};
Z, b - аналогичны L-факторной модели без повторений.
Пусть далее
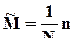 ,
,
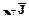 ´
´  -матрица
-матрица  , в частности
, в частности 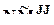 - диагональная NJ- матрица
- диагональная NJ- матрица 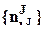 , где
, где 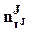 - количество наблюдений при IJ-м сочетании значений факторов J (
- количество наблюдений при IJ-м сочетании значений факторов J ( 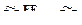 );
);
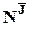 ´
´ 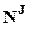 -матрица
-матрица 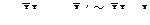 ,
,
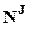 -вектор-столбец
-вектор-столбец 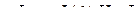 ,
,
где 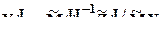 - NJ-вектор-столбец средневзвешенных x по сочетаниям значений факторов J.
- NJ-вектор-столбец средневзвешенных x по сочетаниям значений факторов J.
Матрица M и вектор m системы нормальных уравнений для b составляются естественным образом из блоков 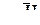 и mJ.
и mJ.
Формулы для MJ (в данном случае MJJ), mJ и XJ, приведенные для модели без повторений, являются частным случаем этих формул при 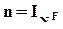 .
.
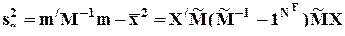 - полная дисперсия в сокращенной модели или объясненная дисперсия в исходной модели.
- полная дисперсия в сокращенной модели или объясненная дисперсия в исходной модели.
Разные эффекты могут оставаться ортогональными ( 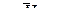 при
при 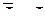 ) в одном специальном случае, когда каждый более младший фактор делит все выделенные до него подгруппы в одинаковых пропорциях, т.е.
) в одном специальном случае, когда каждый более младший фактор делит все выделенные до него подгруппы в одинаковых пропорциях, т.е. 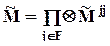 (в частности, когда количество повторений nI для всех сочетаний I одинаково). В этом случае для ортогональности эффектов достаточно матрицы
(в частности, когда количество повторений nI для всех сочетаний I одинаково). В этом случае для ортогональности эффектов достаточно матрицы 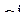 выбрать так, чтобы
выбрать так, чтобы 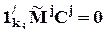 . Эти требования удовлетворяются, если данные матрицы обладают описанной выше (для однофакторной модели с повторениями) структурой:
. Эти требования удовлетворяются, если данные матрицы обладают описанной выше (для однофакторной модели с повторениями) структурой:
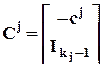 , где
, где 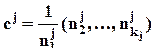 .
.
Такие матрицы обобщают структуру матриц 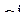 модели без повтрений.
модели без повтрений.
Для этого специального случая можно построить формулы решения задачи дисперсионного анализа, обобщающие приведенные выше формулы для модели без повторений.
В общем случае указанный выбор матриц 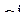 обеспечивает равенство нулю только
обеспечивает равенство нулю только 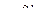 . Особым выбором CJ (p(J)>1) можно добиться равенства нулю еще некоторых блоков общей матрицы M.
. Особым выбором CJ (p(J)>1) можно добиться равенства нулю еще некоторых блоков общей матрицы M.
Матрица CJ не обязательно должна равняться прямому произведению 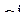 по
по  . Она должна быть размерности
. Она должна быть размерности  ´
´ 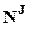 и иметь ранг
и иметь ранг 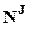 , т.е., например, обладать структурой
, т.е., например, обладать структурой 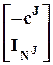 , где cJ -
, где cJ - 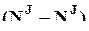 ´
´ 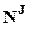 -матрица. Поэтому для определения этой матрицы необходимо иметь
-матрица. Поэтому для определения этой матрицы необходимо иметь 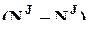 ´
´ 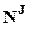 условий. Поскольку
условий. Поскольку
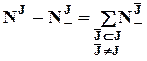 ,
,
нужное количество условий содержат требования

для всех 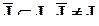 , включая пустое множество
, включая пустое множество 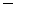 (C0 = 1).
(C0 = 1).
Таким образом, матрицы CJ всегда можно определить так, чтобы эффекты нулевого и высшего порядков были ортогональны друг с другом и с остальными эффектами, и, в частности,  .
.
Дисперсия 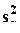 в общем случае не делится на факторные дисперсии, как это было в модели без повторений; точно в ней выделяется только дисперсия эффектов высшего порядка (при указанном выборе CJ):
в общем случае не делится на факторные дисперсии, как это было в модели без повторений; точно в ней выделяется только дисперсия эффектов высшего порядка (при указанном выборе CJ):
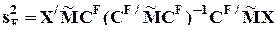 ,
,
и для нее непосредственно можно проверить нулевую гипотезу с помощью F-критерия
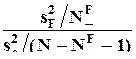 .
.
Нулевые гипотезы для остальных факторных дисперсий имеют вид b J = 0, и в числителе F-статистики помещается величина
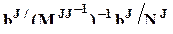 ,
,
где 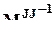 - соответствующий блок матрицы M - 1,
- соответствующий блок матрицы M - 1,
а в знаменателе -
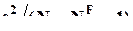 или
или 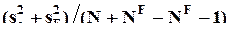 - если нулевая гипотеза для
- если нулевая гипотеза для 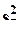 не отвергается.
не отвергается.
Практическое занятие № 4. «Применение Eviews при построении и анализе многофакторной модели регрессии. Выявление мультиколлинеарности и гетероскедастичности в модели. Проверка спецификации модели»
Пример 4. Имеются данные о вариации дохода кредитных организаций США за период 25 лет в зависимости от изменений годовой ставки по сберегательным депозитам и числа кредитных учреждений.
Введем следующие обозначения:
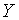 – прибыль кредитных организаций, %;
– прибыль кредитных организаций, %;
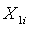 - чистый доход на 1$ депозита;
- чистый доход на 1$ депозита;
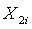 – число кредитных учреждений.
– число кредитных учреждений.
| Год | 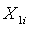 (Income) (Income)
| 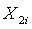 (Credit institutions) (Credit institutions)
| 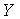 (Profit) (Profit)
|
| 1 | 3,92 | 7298 | 0,75 |
| 2 | 3,61 | 6855 | 0,71 |
| 3 | 3,32 | 6636 | 0,66 |
| 4 | 3,07 | 6506 | 0,61 |
| 5 | 3,06 | 6450 | 0,7 |
| 6 | 3,11 | 6402 | 0,72 |
| 7 | 3,21 | 6368 | 0,77 |
| 8 | 3,26 | 6340 | 0,74 |
| 9 | 3,42 | 6349 | 0,9 |
| 10 | 3,42 | 6352 | 0,82 |
| 11 | 3,45 | 6361 | 0,75 |
| 12 | 3,58 | 6369 | 0,77 |
| 13 | 3,66 | 6546 | 0,78 |
| 14 | 3,78 | 6672 | 0,84 |
| 15 | 3,82 | 6890 | 0,79 |
| 16 | 3,97 | 7115 | 0,7 |
| 17 | 4,07 | 7327 | 0,68 |
| 18 | 4,25 | 7546 | 0,72 |
| 19 | 4,41 | 7931 | 0,55 |
| 20 | 4,49 | 8097 | 0,63 |
| 21 | 4,7 | 8468 | 0,56 |
| 22 | 4,58 | 8717 | 0,41 |
| 23 | 4,69 | 8991 | 0,51 |
| 24 | 4,71 | 9179 | 0,47 |
| 25 | 4,78 | 9318 | 0,32 |
1. Создать файл с исходными данными в среде Excel (файл example _04. xls).
2. Осуществить импорт исходных данных в Eviews.
Создать workfile .
4. Найти значения описательных статистик по каждой переменной и объяснить их (рис. 58).
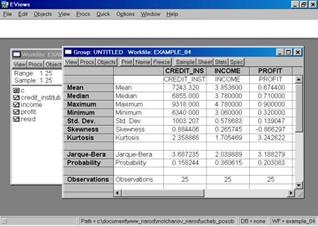
Рис. 58.
5. Построить корреляционную матрицу для всех переменных, включенных в модель (рис. 59).
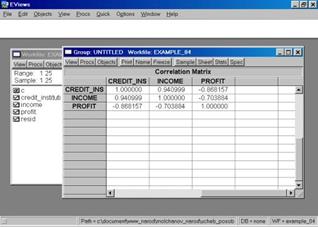
Рис. 59.
6. Построить регрессионное уравнение МНК, в котором зависимая переменная – прибыль кредитных организаций, а независимые – чистый доход на 1$ депозита и число кредитных учреждений (рис. 60, 61).
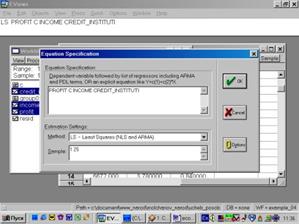
Рис. 60.
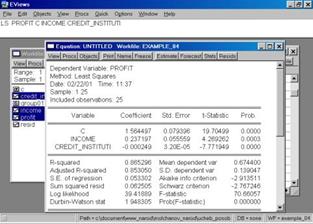
Рис. 61.
Уравнение примет следующий вид:
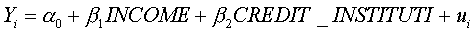 .
.
Подставим полученные оценки из итоговой формы вывода:
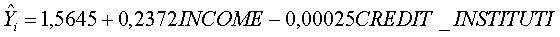 .
.
Дата добавления: 2019-11-25; просмотров: 385; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
