Основная модель линейной регрессии
Введение
Представленный курс посвящен начальному уровню эконометрики — регрессионному анализу. Лекции включают 7 теоретических разделов:
1. Описательная статистика.
2. Случайные ошибки измерения.
3. Алгебра линейной регрессии.
4. Основная модель линейной регрессии.
5. Гетероскедастичность и автокорреляция ошибок.
6. Ошибки измерения факторов и фиктивные переменные.
7. Оценка параметров систем уравнений.
Каждый раздел открывается кратким обзором теоретического материала, затем следует материал для освоения практических заданий. Практикум курса направлен на изучение и освоение практики эконометрики по следующим направлениям:
1. Знакомство с эконометрическим пакетом Econometric Views
2. Построение и анализ парной регрессии
3. Построение и анализ множественной регрессии
4. Использование фиктивных переменных в регрессии
Примеры выполнения практических заданий приводятся с использованием эконометрического пакета Econometric Views (EViews). Подробную информацию об условиях приобретения и распространения пакета можно получить на сайте производителя: http://www.eviews.com.
Все используемые в практикуме задания (примеры) основаны на учебном пособии Молчанов И.Н., Герасимова И.А. Компьютерный практикум по начальному курсу эконометрики (реализация на EViews). Приведенные примеры доступны в виде файлов в формате Excel и EViews по адресу: http://molchanov.narod.ru/econometrics.html .
При выполнении предлагаемых заданий могут оказаться полезными следующие учебники и пособия:
1. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. – М.: ЮНИТИ, 1998. – 1022 с. ISBN 5-238-00013-8.
2. Доугерти К. Введение в эконометрику. - М.: ИНФРА-М, 1997. – XIV, 402 с.: ил. - (Университетский учебник) Библиография: с.384-386. ISBN 5-86225-458-7; 0-19-50346-4.
3. Елисеева И.И. Эконометрика: Учебник /И.И.Елисеева и др. – М.: Финансы и статистика, 2001. – ISBN 5-279-01955-0.
4. Князевский В.С., Житников И.В. Анализ временных рядов и прогнозирование: Учеб. пособие. – Ростов-на-Дону: РГЭА, 1998. – 161 с.
5. Князевский В.С., Молчанов И.Н. Статистические расчеты на компьютере с использованием ППП Microstat. - Ростов-на-Дону: РГЭА, 1996. - 86 с.
6. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. – М.: Дело, 2000. – 400 с. ISBN 5-7749-0055-X.
7. Практикум по эконометрике: Учеб. пособие /И.И.Елисеева и др. – М.: Финансы и статистика, 2001. – 192 с. ISBN 5-279-02313-2.
8. Greene, W.H. Econometric analysis, Prentice Hall, 4th Edition, 2000. – 1004 pages.
9. Verbeek, M. A Guide to Modern Econometrics, Wiley, 2000. – 400 pages.
Лекция 1. Основы описательной статистики.
Описательная статистика
1.1. Ряды наблюдений и их характеристики
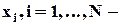 ряд наблюдений за непрерывной случайной переменной x, вариационный ряд, выборка.
ряд наблюдений за непрерывной случайной переменной x, вариационный ряд, выборка.
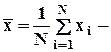 среднеарифметическое значение;
среднеарифметическое значение; 
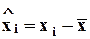 - центрированные значения наблюдений;
- центрированные значения наблюдений;
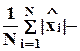 среднее линейное отклонение;
среднее линейное отклонение;
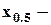 медиана, т.е. среднее значение в ряду наблюдений:
медиана, т.е. среднее значение в ряду наблюдений:
если 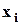 упорядочены по возрастанию, то она равна
упорядочены по возрастанию, то она равна 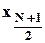 при N нечетном и
при N нечетном и 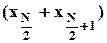 при N четном;
при N четном;

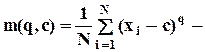 моменты q-го порядка, центральные при
моменты q-го порядка, центральные при 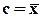 , начальные при
, начальные при 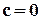 .
.

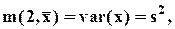 дисперсия x ,
дисперсия x ,
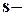 среднеквадратическое (стандартное) отклонение,
среднеквадратическое (стандартное) отклонение,
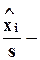 центрированные и нормированные значения наблюдений,
центрированные и нормированные значения наблюдений, 
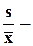 коэффициент вариации,
коэффициент вариации,
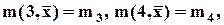
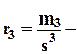 показатель асимметрии, если
показатель асимметрии, если 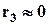 , то распределение величины симметрично, если
, то распределение величины симметрично, если 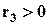 , то имеет место правая асимметрия, если
, то имеет место правая асимметрия, если 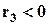 , - левая асимметрия;
, - левая асимметрия;
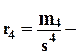 показатель эксцесса (куртозиса), если
показатель эксцесса (куртозиса), если 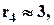 то распределение близко к нормальному, если
то распределение близко к нормальному, если  то распределение высоковершинное, если
то распределение высоковершинное, если 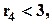 - низковершинное.
- низковершинное.
Пусть наряду с величиной x имеется N наблюдений yi за величиной y.
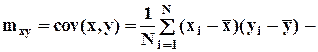 ковариация x и y,
ковариация x и y,
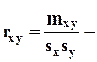 коэффициент корреляции x и y;
коэффициент корреляции x и y;  если
если 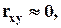 то величины x и y линейно независимы, если
то величины x и y линейно независимы, если 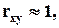 то они положительно линейно зависимы, если
то они положительно линейно зависимы, если 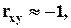 - отрицательно линейно зависимы.
- отрицательно линейно зависимы.
1.2. Эмпирические распределения случайной величины
Пусть все 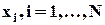 попадают в полуинтервал
попадают в полуинтервал 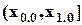 , который делится на k равных полуинтервалов длиной
, который делится на k равных полуинтервалов длиной 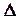 ;
;  . (предполагается, что
. (предполагается, что 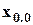 “чуть” меньше или равно
“чуть” меньше или равно 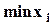 , а
, а 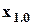 “чуть” больше или равно
“чуть” больше или равно 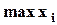 , так что некоторые из
, так что некоторые из 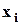 попадают как в 1-й, так и в последний из этих k полуинтервалов).
попадают как в 1-й, так и в последний из этих k полуинтервалов).
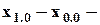 общий размах вариации.
общий размах вариации.
 оптимальное соотношение между k и N (формула Стерджесса).
оптимальное соотношение между k и N (формула Стерджесса).
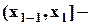 l -й полуинтервал
l -й полуинтервал 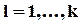 , где
, где
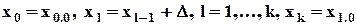 .
.
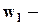 доля общего количества наблюдений N , попавших в l-й полуинтервал - частоты, эмпирические оценки вероятностей попадания в данный полуинтервал;
доля общего количества наблюдений N , попавших в l-й полуинтервал - частоты, эмпирические оценки вероятностей попадания в данный полуинтервал;
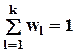 ;
;
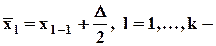 центры полуинтервалов;
центры полуинтервалов;
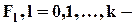 накопленные частоты (эмпирические вероятности, с которыми значения величины в выборке не превышают xl ):
накопленные частоты (эмпирические вероятности, с которыми значения величины в выборке не превышают xl ):
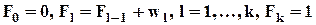 ;
;
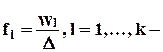 эмпирические плотности распределения вероятности.
эмпирические плотности распределения вероятности.
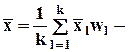 среднеарифметическое значение;
среднеарифметическое значение;
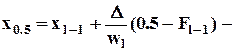 медиана, здесь l-й полуинтервал является медианным, т.е.
медиана, здесь l-й полуинтервал является медианным, т.е. 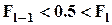 ;
;
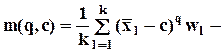 моменты q-го порядка;
моменты q-го порядка;
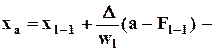 a-й (a100-процентный) квантиль, т.е. значение величины, которое не превышается в выборке с вероятностью a; здесь l-й полуинтервал является квантильным, т.е.
a-й (a100-процентный) квантиль, т.е. значение величины, которое не превышается в выборке с вероятностью a; здесь l-й полуинтервал является квантильным, т.е. 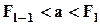 (
( 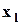 являются квантилями с
являются квантилями с 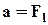 );
);
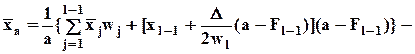 среднее по той (нижней) части выборки, которая выделяется a-м квантилем (l-й полуинтервал также квантильный).
среднее по той (нижней) части выборки, которая выделяется a-м квантилем (l-й полуинтервал также квантильный).
Среди квантилей особое значение имеют те, которые делят выборку на равные части (иногда именно эти величины называют квартилями):
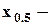 медиана;
медиана;
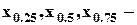 квартили;
квартили;
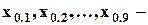 децили;
децили;
 процентили.
процентили.
 децильный размах вариации (может быть также квартильным или процентильным);
децильный размах вариации (может быть также квартильным или процентильным);
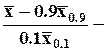 децильный коэффициент вариации (может быть медианным, квартильным или процентильным).
децильный коэффициент вариации (может быть медианным, квартильным или процентильным).
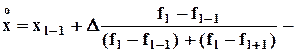 мода, т.е. наиболее вероятное значение величины в выборке; здесь l-й полуинтервал является модальным, fl на нем достигает максимума; если этот максимум единственный, то распределение величины называется унимодальным; если максимума два - бимодальным; в общем случае - при нескольких максимумах - полимодальным.
мода, т.е. наиболее вероятное значение величины в выборке; здесь l-й полуинтервал является модальным, fl на нем достигает максимума; если этот максимум единственный, то распределение величины называется унимодальным; если максимума два - бимодальным; в общем случае - при нескольких максимумах - полимодальным.
Гистограмма - эмпирическая (интервальная) функция плотности распределения; имеет ступенчатую форму: на l-м полуинтервале (l=1,...,k) принимает значение fl;
Полигон - функция, график которой образован отрезками, соединяющими точки 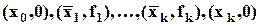 .
.
Гистограмма и полигон могут строиться непосредственно по весам wl, если (как в данном случае) все полуинтервалы 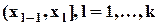 имеют одинаковую длину.
имеют одинаковую длину.
Кумулята - эмпирическая (интервальная) функция распределения вероятности, график которой образован отрезками, соединяющими точки 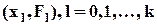 .
.
Огива - то же, что и кумулята, или (в традициях советской статистики) функция, обратная кумуляте.
1.3. Теоретические функции распределения случайной величины
x - случайная величина,
z - детерминированная переменная.
 функция распределения вероятности x;
функция распределения вероятности x;
 функция плотности распределения вероятности x;
функция плотности распределения вероятности x;
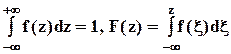 ,
,
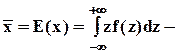 математическое ожидание, среднее (теоретическое);
математическое ожидание, среднее (теоретическое);
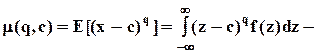 моменты q-го порядка (теоретические);
моменты q-го порядка (теоретические);
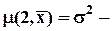 дисперсия (теоретическая);
дисперсия (теоретическая);
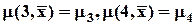 ;
;
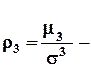 показатель асимметрии (теоретический),
показатель асимметрии (теоретический),
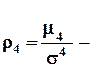 показатель эксцесса, куртозиса (теоретический).
показатель эксцесса, куртозиса (теоретический).
Для квантиля 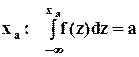 ; для моды
; для моды 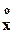 : максимум
: максимум 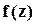 достигается при
достигается при 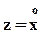 .
.
Если распределение случайной величины симметрично, то 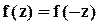 и
и 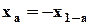 . В этом случае можно использовать понятие двустороннего квантиля
. В этом случае можно использовать понятие двустороннего квантиля 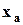 , для которого
, для которого 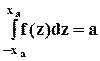 , и значение которого совпадает с
, и значение которого совпадает с 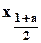 - значением обычного (одностороннего) квантиля.
- значением обычного (одностороннего) квантиля.
Если распределение случайной величины унимодально, то в случае симметричности 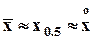 , при правой асимметрии
, при правой асимметрии  , при левой асимметрии
, при левой асимметрии 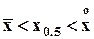 .
.
1.4. Функции распределения, используемые в эконометрике
В силу центральной предельной теоремы математической статистики, ошибки измерения и “остатки”, необъясняемые “хорошей” эконометрической моделью, имеют распределения близкие к нормальному. Поэтому все распределения, используемые в классической эконометрии, основаны на нормальном.
Пусть 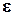 - случайная величина, имеющая нормальное распределение с нулевым мат.ожиданием и единичной дисперсией (
- случайная величина, имеющая нормальное распределение с нулевым мат.ожиданием и единичной дисперсией ( 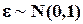 ). Функция плотности распределения ее прямо пропорциональна
). Функция плотности распределения ее прямо пропорциональна 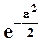 (для наглядности в записи функции плотности вместо z использован символ-имя самой случайной величины); 95-процентный двусторонний квантиль
(для наглядности в записи функции плотности вместо z использован символ-имя самой случайной величины); 95-процентный двусторонний квантиль 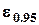 равен 1.96, 99-процентный квантиль - 2.57.
равен 1.96, 99-процентный квантиль - 2.57.
Пусть теперь имеется k таких взаимно независимых величин 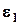
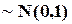 . Сумма их квадратов
. Сумма их квадратов 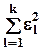 является случайной величиной, имеющей распределение
является случайной величиной, имеющей распределение 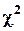 c k степенями свободы (обозначается
c k степенями свободы (обозначается 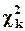 ). 95-процентный (односторонний) квантиль
). 95-процентный (односторонний) квантиль 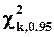 при k=1 равен 3.84 (квадрат 1.96), при k=5 - 11.1, при k=20 - 31.4, при k=100 - 124.3.
при k=1 равен 3.84 (квадрат 1.96), при k=5 - 11.1, при k=20 - 31.4, при k=100 - 124.3.
Если две случайные величины 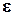 и
и 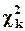 независимы друг от друга, то случайная величина
независимы друг от друга, то случайная величина 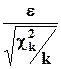 имеет распределение t -Стъюдента с k степенями свободы (
имеет распределение t -Стъюдента с k степенями свободы ( 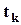 ). Ее функция распределения прямо пропопорциональна
). Ее функция распределения прямо пропопорциональна 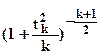 ; в пределе при
; в пределе при 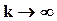 она становится нормально распределенной. 95-процентный двусторонний квантиль
она становится нормально распределенной. 95-процентный двусторонний квантиль 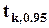 при k=1 равен 12.7, при k=5 - 2.57, при k=20 - 2.09, при k=100 - 1.98 .
при k=1 равен 12.7, при k=5 - 2.57, при k=20 - 2.09, при k=100 - 1.98 .
Если две случайные величины 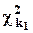 и
и  не зависят друг от друга, то случайная величина
не зависят друг от друга, то случайная величина 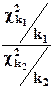 имеет распределение F-Фишера с k1 и k2 степенями свободы (
имеет распределение F-Фишера с k1 и k2 степенями свободы ( 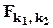 ). 95-процентный (односторонний) квантиль
). 95-процентный (односторонний) квантиль 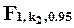 при k2=1 равен 161, при k2=5 - 6.61, при k2=20 - 4.35, при k2=100 - 3.94 (квадраты соответствующих
при k2=1 равен 161, при k2=5 - 6.61, при k2=20 - 4.35, при k2=100 - 3.94 (квадраты соответствующих 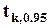 ); квантиль
); квантиль 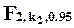 при k2=1 равен 200, при k2=5 - 5.79, при k2=20 - 3.49, при k2=100 - 3.09; квантиль
при k2=1 равен 200, при k2=5 - 5.79, при k2=20 - 3.49, при k2=100 - 3.09; квантиль 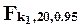 при k1=3 равен 3.10, при k1=4 - 2.87, при k1=5 - 2.71, при k1=6 - 2.60.
при k1=3 равен 3.10, при k1=4 - 2.87, при k1=5 - 2.71, при k1=6 - 2.60.
Случайные ошибки измерения
2.1. Первичные измерения
Путсь имеется N измерений xi, i = 1,...,N случайной величины x. Это - наблюдения за случайной величиной. Предполагается, что измерения проведены в неизменных условиях (факторы, влияющие на x, не меняют своих значений), и систематические ошибки измерений исключены. Тогда различия в результатах отдельных наблюдений (измерений) связаны только с наличием случайных ошибок:
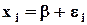 ,
,
где 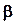 - истинное значение x,
- истинное значение x,
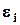 - случайная ошибка в i-м наблюдении.
- случайная ошибка в i-м наблюдении.
Если x и e - вектора-столбцы, соответственно, xi и e i, а 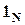 - N-компонентный вектор-столбец, состоящий из единиц, то данную модель можно записать в матричной форме:
- N-компонентный вектор-столбец, состоящий из единиц, то данную модель можно записать в матричной форме:
x 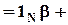 e.
e.
Предполагается, что ошибки по наблюдениям не зависят друг от друга и 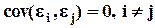 , а их дисперсии по наблюдениям одинаковы
, а их дисперсии по наблюдениям одинаковы  , или в матричной форме E( ee / ) = IN s 2 (где IN - единичная матрица размерности N). Требуется найти b и
, или в матричной форме E( ee / ) = IN s 2 (где IN - единичная матрица размерности N). Требуется найти b и 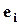 - оценки, соответственно, b и e i. Для этого используется метод наименьших квадратов (МНК), т.е. искомые оценки определяются так, чтобы
- оценки, соответственно, b и e i. Для этого используется метод наименьших квадратов (МНК), т.е. искомые оценки определяются так, чтобы 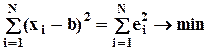 или e/e ® min, где e вектор-столбец оценок
или e/e ® min, где e вектор-столбец оценок 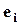 . В результате,
. В результате,
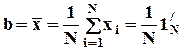 x, e = x
x, e = x 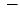 1Nb,
1Nb,
т.е. МНК-оценкой истинного значения измеряемой величины является среднее арифметическое по наблюдениям. Оценка b относится к классу линейных, поскольку линейно зависит от наблюдений за случайной величиной.
В рамках сделанных предположний доказывается, что
- b является несмещенной оценкой b (b = E( b )), ее дисперсия 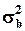 равна
равна 
 и является минимальной на множестве линейных оценок; класс таких оценок (процедур оценивания) называют BLUE - Best Linear Unbiased Estimators;
и является минимальной на множестве линейных оценок; класс таких оценок (процедур оценивания) называют BLUE - Best Linear Unbiased Estimators;
- несмещенной оценкой s 2 является
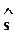 2
2 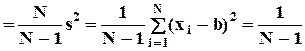 e/e .
e/e .
Пусть теперь e i распределены нормально, тогда оценка максимального правдоподобия b совпадает с b, она несмещена, состоятельна (в пределе при 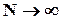 совпадает с b и имеет нулевую дисперсию) и эффективна (имеет минимально возможную дисперсию), величина
совпадает с b и имеет нулевую дисперсию) и эффективна (имеет минимально возможную дисперсию), величина 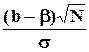 имеет распределение N(0,1) и (1- q )100-процентный доверительный интервал для b определяется как
имеет распределение N(0,1) и (1- q )100-процентный доверительный интервал для b определяется как
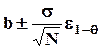 ,
,
где e 1- q - (1- q )100-процентный двусторонний квантиль нормального распределения.
Эта формула для доверительного интервала используется, если известно точное значение s .
На практике точное значение s, как правило,неизвестно, и используется другой подход.
Величина 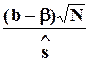 имеет распределение
имеет распределение 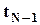 и (1- q )100-процентный доверительный интервал для b строится как
и (1- q )100-процентный доверительный интервал для b строится как
 ,
,
где tN-1,1- q - (1- q )100-процентный двусторонний квантиль tN-1-распределения.
Поскольку величина b детерминирована, доверительные интервалы интерпретируются следующим образом: если процедуру построения доверительного интервала повторять многократно, то (1- q )100 процентов полученных интервалов будут содержать истинное значение b измеряемой величины.
2.2. Производные измерения
Пусть xj, j = 1,...,n - выборочные (фактические) значения (наблюдения, измерения) n различных случайных величин, b j - их истинные значения, e j - ошибки измерений. Если x, b, e - соответствующие n-компонентные вектора-строки, то
x = b + e.
Предполагается, что E( e ) = 0, и ковариационная матрица ошибок E( e / e ) равна W.
Пусть величина y рассчитывается как f(x). Требуется найти дисперсию 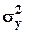 ошибки e y =
ошибки e y = 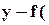 b ) измерения (расчета) этой величины.
b ) измерения (расчета) этой величины.
Разложение функции f в ряд Тэйлора в фактической точке x по направлению b - x (= -e), если в нем оставить только члены 1-го порядка, имеет вид:
f( b ) = y - e g или e y = e g (заменяя “»“ на “=“),
где g - градиент f в точке x (вектор-столбец с компонентами gj = 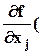 x)).
x)).
Откуда  и
и
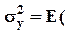 g/ e / e g) = g/ W g,
g/ e / e g) = g/ W g,
Это - общая формула, частным случаем которой являются известные формулы для дисперсии среднего, суммы, разности, произведения, частного от деления и др.
В случае, если ошибки величин xj не скоррелированы друг с другом и имеют одинаковую дисперсию s 2,
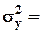 g/g s 2.
g/g s 2.
В случае, если известны только дисперсии ошибок e j, можно воспользоваться формулой, дающей верхнюю оценку дисперсии ошибки результата вычислений:
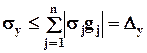 ,
,
где s j - среднеквадратическое отклонение e j.
Практическое занятие №1.
«Знакомство с эконометрическим пакетом Econometric Views»
Эконометрический пакет Eviews обеспечивает особо сложный и тонкий инструментарий обработки данных, позволяет выполнять регрессионный анализ, строить прогнозы в Windows-ориентированной компьютерной среде. С помощью этого программного средства можно очень быстро выявить наличие статистической зависимости в анализируемых данных и затем, используя полученные взаимосвязи, сделать прогноз изучаемых показателей. Особо широкие возможности открывает Eviews при анализе данных, представленных в виде временных рядов.
Eviews (далее пакет) установлен в директорий Program Files / Eviews 3. Запуск осуществляется выбором соответствующего значка в панели Пуск/Программы/Eviews 3/ Eviews 3.1 (файл C:\Program Files\EViews3\EViews3.exe) (см. рис. 1) или щелчком (двойным щелчком – в зависимости от установок) по соответствующей пиктограмме на рабочем столе.
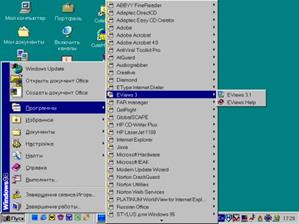
Рис. 1.
Если Вы все сделали правильно, появится стартовое окно пакета (рис.2).

Рис. 2.
Если в настоящий момент окно, содержащее пакет, является активным, то первая строка экрана (Title Bar) будет темнее остальных. При переключении в другое окно цветовая окраска данной строки изменит цвет на более приглушенный (серый).
Ниже следует строка основного меню (Main Menu). Принцип его построения прост – при нажатии на соответствующие клавиши появляется раскрывающееся меню (drop - down menu). Доступные в настоящий момент опции являются затемненными (darkened menu items). Те пункты, с которыми в настоящий момент работа невозможна, приглушены (grayed menu items).
Далее располагается командная строка (окно) (command window). В нем происходит непосредственный набор команд, которые выполняются после нажатия клавиши Enter (Ввод). Для исполнения многих команд отсутствует необходимость их набора – просто надо выбрать нужный пункт в основном меню.
Большая часть экрана пакета отведена под рабочую область (work area). В ней размещаются рабочие объекты. Переключение между ними осуществляется нажатием клавиши F 6.
Последняя область экрана показывает текущее состояние (status line) пакета (рабочий каталог, текущий файл и др.).
Завершение работы с пакетом осуществляется путем выбора в командной строке опции File / Exit. Система предложит сохранить/не сохранить имеющиеся данные. Если имя файла не было задано ранее, автоматически будет предложено имя UNTITLED. Его можно изменить на любое другое. Пакет имеет обширную справочную систему (пункт основного меню Help).
Знакомство с пакетом начнем с файла, содержащего данные о совокупном спросе на деньги (M1) – (aggregate money demand) (M 1) – зависимая переменная; независимые: доход (ВВП) - income (GDP); уровень цен (PR) - price level (PR); краткосрочная процентная ставка (RS) - short term interest rate (RS).
Проведем некоторые преобразования и расчеты.
Первым шагом создадим новый рабочий файл (workfile). Его имя должно иметь следующий вид и состоять только из латинских букв: Номер_группы_ demo _01. wf1 (расширение wf1 присваивается автоматически). Например: 451_ demo _01. wf 1. Расположить его следует в директории, относящемся к Вашему факультету (внимательно ознакомьтесь с памяткой в компьютерном классе). Исходные данные находятся в файле Excel. Они должны быть импортированы в пакет. Создание рабочего файла начнем с того, что выберем File / New / Workfile в основном меню (см. рис. 3).
После нажатия на кнопке со словом Workfile откроется диалоговое окно, с помощь которого можно задать тип вводимых Вами данных (см. рис. 4).
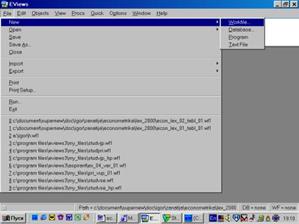
Рис. 3.
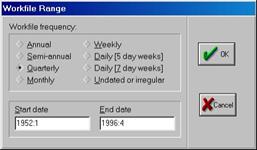
Рис. 4.
Как видно из рис. 4, в пакете допускается восемь типов данных. Это могут быть:
Годовые (Annual) – годы 20 в. идентифицируются по последним двум цифрам (97 эквивалентно 1997), для данных, относящихся к 21 в. необходима полная идентификация (например, 2020);
Полугодовые (Semi-annual) – 1999:1, 2001:2 (формат – год и номер полугодия);
Квартальные (Quarterly) – 1992:1, 65:4, 2005:3 (формат – год и номер квартала);
Ежемесячные (Monthly) – 1956:1, 1990:11 (формат – год и номер месяца);
Недельные (Weekly) и дневные (5/7 day weeks) – допускаются форматы Месяц/День/Год (по умолчанию) и (День/Месяц/Год) – настроить эту опцию можно в меню Options / Frequency Conversion & Date Display. Так, введенные числа 8:10:97 будут интерпретированы как Август, 10, 1997. Для установки, принятой в Европе, начальная дата будет выглядеть как Октябрь, 8, 1997;
Недатированные или нерегулярные (Undated or irregular) – допускают работу с данными, строго не привязанными к определенным временным периодам.
Важным является указание начальной (start) и конечной (end) даты/наблюдения (date/observation).
В нашем примере начальным периодом является первый квартал 1952 г. (1952:1), конечным – четвертый квартал 1996 г. (1996:4).
Закончив ввод временных периодов, надо нажать клавишу OK. Пакет создаст рабочий файл без имени, и на дисплее в рабочей области появится окно (см. рис. 5). Все рабочие файлы пакета всегда содержат вектор коэффициентов C и серию RESID.
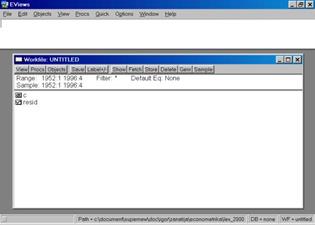
Рис. 5.
Следующим шагом является просмотр исходных данных, содержащихся в исходном файле по адресу Program Files / Eviews 3/ Example files / demo . xls (формат Exсel версии 5.0 и младше). Важное замечание: имеющаяся версия пакета позволяет импортировать файлы Excel не старше версии 5.0. В противном случае будет выдано сообщение об ошибке. Всегда сохраняйте свои файлы как файлы Microsoft Excel 5.0/95. Для визуализации данных необходимо запустить табличный процессор Excel (действия аналогичны запуску Eviews). Результат представлен на рис. 6. Ознакомившись с данными, файл, подлежащий экспортированию, необходимо закрыть.
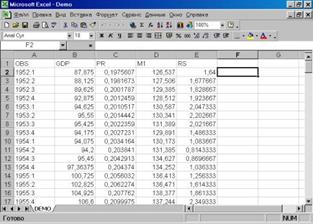
Рис. 6.
Для чтения данных, созданных в других программах, надо выбрать в рабочем файле опцию Procs/Import/Read Text-Lotus-Excel… (см. рис. 7). Появится диалог, представленный на рис. 8.

Рис. 7.
Перейдем к папке, содержащей искомый файл (для упрощения поиска в опции Тип файлов (Files of type) можно выбрать Excel . xls (см. рис.8). Для того, чтобы пакет «помнил» Ваши перемещения по папкам компьютера, можно поставить флажок в опции Update default directory (см. рис. 8).
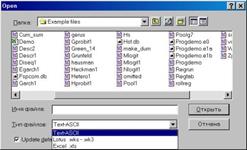
Рис. 8.
Наведем курсор на файл demo . xls и нажмем кнопку Открыть (см. рис. 8). Появится диалог открытия электронных таблиц формата Excel (см. рис. 9).
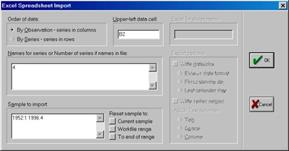
Рис. 9.
По умолчанию в окне, представленном на рис. 9, предполагается, что данные находятся в столбцах (by observation - series in columns). Если данные представлены в виде серий в строках, то надо отметить другую опцию (By series - series in rows).
Окно Upper - left data cell (левая верхняя ячейка данных) автоматически отобразило клетку B 2. Это означает, что данные будут импортироваться из исходной таблицы с клетки, указанной в этом окне (тем самым первая строка и первый столбец будут пропущены). Это вполне соответствует структуре нашего исходного файла (см. рис. 6). Иногда приходится исправлять адрес такой клетки на актуальный.
В окне Names for series or Number of series if names in file (имена для серий или число серий, если имена содержатся в файле) указываем цифру 4. Это связано с тем, что исходный файл (см. рис.6) содержит 4 переменные, находящиеся в столбцах. Имена для этих переменных будут взяты из первой строки электронной таблицы (клетки B1:E1). В том случае, когда необходимо импортировать часть данных (например, только первые две переменные), надо ввести их количество (цифра 2). Если имена переменных, по каким либо причинам, в исходном файле не заданы, можно вместо цифр ввести их имена (латинскими буквами). Если количество переменных, введенных в рассматриваемом окне, превышает количество реально существующих, то в рабочий файл будет введен столбец с заданным именем без данных (обозначаются такие клетки как NA). Если все другие установки удовлетворяют заданным Вами условиям, то можно нажать кнопку OK. Появится окно, отображенное на рис. 10.
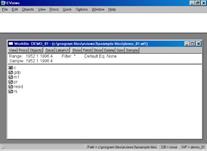
Рис. 10.
После того, как исходные данные перенесены Вами в рабочую область пакета (появились имена переменных), надо провести их верификацию (проверку правильности). Вам необходимо создать новую группу, содержащую все импортированные серии (переменные). Это делается следующим образом: необходимо кликнуть мышкой по имени первой переменной (например, GNP), затем, удерживая клавишу CTRL кликнуть по переменным M1, PR и RS. Все серии на экране будут зачернены. Затем необходимо подвести курсор мыши на зачерненную область экрана и кликнуть правой кнопкой. Далее необходимо выбрать опцию Open. Пакет откроет диалоговое окно со следующими опциями (см. рис. 11).
Выберем Open Group (открыть в одной группе). Пакет создаст группу с именем UNTITLED, в которую войдут все переменные (серии). По умолчанию, данные будут представлены в виде электронной таблицы (возможны другие варианты представления) – см. рис. 12.
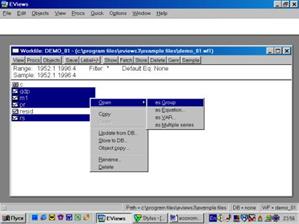
Рис. 11.
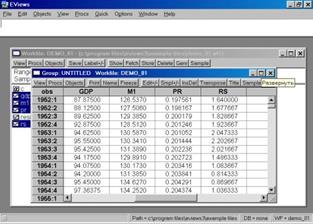
Рис. 12.
Проведите визуальную проверку корректности данных. Сравните, как разместились переменные из исходного файла, обратите внимание на столбец слева от первой переменной (он серого цвета). В нем отображены годы и порядковые номера кварталов. Полученной новой группе данных можно дать имя. Для этого необходимо нажать кнопку Name в текущем окне (см. рис. 12). Появится диалоговое окно (рис. 13.). Автоматически будет предложено имя – GROUP 01. Его можно принять, нажав кнопку OK . В рабочем файле сразу добавится одна переменная с введенным Вами именем. Теперь к ней всегда можно перейти простым нажатием клавиши мыши.
Рис. 13.
Образованную Вами группу можно просматривать не только в виде электронной таблицы. Если, находясь внутри GROUP 01, выбрать последовательность команд View / Multiple Graphs / Line (см. рис. 14), то данные предстанут не в виде таблицы, а как линейные графики по каждой серии (переменной) – см. рис. 15.
Рис. 14.
Для того, чтобы вернуться к прежней форме представления данных (например, электронной таблице), надо выбрать View / Spreadsheet.
Для просмотра числовых характеристик (описательных статистик) отмеченных переменных необходимо выбрать в рабочем файле View / Descriptive Stats / Individual Samples (см. рис. 16).
В результате появится окно, представленное на рис. 17. В нем содержатся:
Mean – Среднее арифметическое значение;
Median – Медиана;
Maximum – Максимальное значение;
Minimum – Минимальное значение;
Std . Dev. – Стандартное отклонение (среднее квадратическое отклонение);
Skewness – Коэффициент асимметрии;
Kurtosis – Эксцесс;
Probability –Вероятность;
Observations – Количество наблюдений.
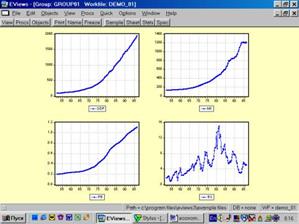
Рис . 15.
Рис . 16.
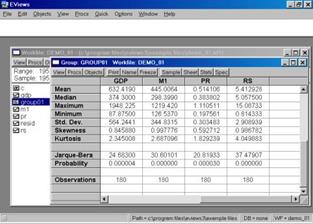
Рис. 17.
Если возникает необходимость проанализировать матрицу коэффициентов корреляции, то необходимо выбрать View / Correlations. Результат представлен на рис. 18.
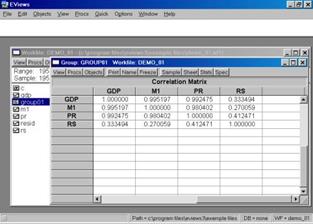
Рис. 18.
Вы также можете исследовать характеристики для отдельных серий (переменных), совместив вывод диаграммы и числовых характеристик. Дважды кликните на имени серии (например, на переменной М1) и выберете в рабочем файле пункт меню View/Descriptive Stats/Histogram and Stats (см. рис. 19). Результат наглядно виден на рис. 20.
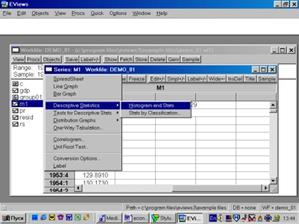
Рис. 19.

Рис. 20.
С другими возможностями пакета Вы познакомитесь на последующих занятиях.
Для индивидуальной работы по предложенной выше схеме предназначены нижеследующие данные. Подумайте, все ли данные необходимо заносить в электронную таблицу или импортировать из неё.
Пример 1. Стоимость однокомнатных квартир в Москве [6].
Данные из газеты «Из рук в руки» за период с декабря 1996 г. по сентябрь 1997г.
Была выбрана Юго-Западная часть города, в которой высок спрос на жилые площади (всего 69 наблюдений). Файл example _01. xls.
Переменные:
N - Номер по порядку.
distc Удаленность. от центра, км.
distm Удаленность от метро, мин.
totsq Общая площадь квартиры, кв.м.
kitsq Площадь кухни, кв.м.
livsq Площадь комнаты, кв.м.
floor Этаж. 0-первый/последний, 1-нет.
cat Категория дома. 1-кирпичный, 0-нет.
price Цена квартиры, тыс. USD.
Найдите среднее арифметическое, выборочное стандартное отклонение и другие статистики параметров. Найдите коэффициенты корреляции параметров с ценой квартиры. Соответствуют ли полученные значения экономической интуиции?
| N | region | distc | distm | totsq | kitsq | livsq | floor | cat | price |
| 1 | Фрунзенская | 4 | 10 | 34,00 | 7,50 | 19,00 | 1 | 1 | 54 |
| 2 | Ленинский пр. | 5,7 | 7 | 36,00 | 10,00 | 20,00 | 0 | 0 | 35 |
| 3 | Ленинский пр. | 5,7 | 12 | 45,00 | 13,00 | 20,00 | 1 | 1 | 59 |
| 4 | Академическая | 7,6 | 10 | 35,30 | 10,00 | 20,00 | 1 | 0 | 35 |
| 5 | Университет | 8,7 | 6 | 33,00 | 5,50 | 22,00 | 1 | 0 | 33 |
| 6 | Нов.Черемуш. | 10,3 | 3 | 33,00 | 8,50 | 18,00 | 1 | 1 | 57 |
| 7 | Юго-Западная | 13,3 | 10 | 37,00 | 10,00 | 19,00 | 1 | 0 | 43 |
| 8 | Коньково | 14,8 | 2 | 38,00 | 8,50 | 19,10 | 1 | 0 | 39 |
| 9 | Фрунзенская | 4 | 15 | 54,00 | 9,20 | 27,20 | 1 | 1 | 70 |
| 10 | Университет | 8,7 | 15 | 35,00 | 6,00 | 20,00 | 0 | 1 | 43 |
| 11 | Пр.Вернадск. | 11,4 | 10 | 31,40 | 5,20 | 21,30 | 1 | 0 | 33 |
| 12 | Ленинский пр. | 5,7 | 7 | 32,00 | 6,00 | 21,00 | 1 | 0 | 37 |
| 13 | Нов.Черемуш | 10,3 | 7 | 38,00 | 8,00 | 19,00 | 0 | 0 | 33 |
| 14 | Университет | 8,7 | 10 | 31,60 | 8,80 | 14,00 | 0 | 0 | 31 |
| 15 | Юго-Запад | 13,3 | 5 | 32,00 | 8,00 | 17,00 | 1 | 0 | 37 |
| 16 | Юго-Запад | 13,3 | 10 | 37,00 | 10,00 | 19,00 | 1 | 0 | 43 |
| 17 | Ленинский пр. | 5,7 | 5 | 32,00 | 8,00 | 17,00 | 1 | 1 | 38 |
| 18 | Академическая | 7,6 | 10 | 37,00 | 8,00 | 19,00 | 1 | 1 | 51 |
| 19 | Академическая | 7,6 | 15 | 32,20 | 6,50 | 17,00 | 0 | 1 | 30 |
| 20 | Коньково | 14,8 | 3 | 33,00 | 8,00 | 19,00 | 1 | 0 | 30 |
| 21 | Коньково | 14,8 | 5 | 37,50 | 9,60 | 19,80 | 1 | 0 | 36 |
| 22 | Коньково | 14,8 | 10 | 33,00 | 7,00 | 19,00 | 1 | 0 | 33 |
| 23 | Университет | 8,7 | 15 | 32,00 | 6,00 | 21,50 | 1 | 0 | 35 |
| 24 | Пр.Вернадск. | 11,4 | 5 | 29,70 | 6,00 | 16,10 | 0 | 0 | 28 |
| 25 | Пр.Вернадск. | 11,4 | 15 | 36,00 | 8,60 | 18,00 | 0 | 0 | 40 |
| 26 | Юго-Запад | 13,3 | 15 | 36,00 | 10,00 | 19,00 | 0 | 0 | 33 |
| 27 | Ленинский пр. | 5,7 | 2 | 31,60 | 6,00 | 21,60 | 1 | 1 | 35 |
| 28 | Ленинский пр | 5,7 | 5 | 52,00 | 12,00 | 34,00 | 1 | 1 | 75 |
| 29 | Коньково | 14,8 | 3 | 36,00 | 10,00 | 19,00 | 1 | 0 | 40 |
| 30 | Коньково | 14,8 | 5 | 33,00 | 8,00 | 18,00 | 1 | 0 | 30 |
| 31 | Университет | 8,7 | 5 | 32,00 | 5,50 | 20,10 | 1 | 0 | 31 |
| 32 | Академическая | 7,6 | 15 | 35,00 | 9,80 | 20,00 | 1 | 0 | 37 |
| 33 | Нов.Черемуш | 10,3 | 15 | 38,00 | 10,00 | 19,50 | 1 | 0 | 40 |
| 34 | Коньково | 14,8 | 1 | 39,00 | 8,50 | 19,00 | 1 | 0 | 40 |
| 35 | Фрунзенская | 4 | 5 | 34,00 | 8,00 | 19,00 | 1 | 1 | 58 |
| 36 | Фрунзенская | 4 | 10 | 38,00 | 6,50 | 18,00 | 0 | 1 | 48 |
| 37 | пр.Вернадск. | 11,4 | 3 | 35,00 | 10,00 | 20,00 | 1 | 0 | 40 |
| 38 | Юго-запад | 13,3 | 7 | 36,00 | 9,00 | 19,50 | 1 | 0 | 42 |
| 39 | Нов.Черемуш. | 10,3 | 7 | 34,00 | 8,00 | 18,00 | 1 | 1 | 51 |
| 40 | Коньково | 14,8 | 5 | 38,00 | 8,50 | 19,00 | 1 | 0 | 43 |
| 41 | Коньково | 14,8 | 7 | 33,00 | 6,00 | 19,00 | 1 | 0 | 30 |
| 42 | Коньково | 14,8 | 10 | 32,00 | 8,00 | 17,00 | 1 | 0 | 40 |
| 43 | Коньково | 14,8 | 10 | 38,00 | 8,50 | 19,10 | 1 | 0 | 43 |
| 44 | Академическая | 7,6 | 5 | 43,00 | 8,50 | 25,00 | 0 | 1 | 53 |
| 45 | Академическая | 7,6 | 10 | 30,00 | 6,00 | 18,30 | 1 | 1 | 28 |
| 46 | Коньково | 14,8 | 7 | 34,80 | 7,80 | 17,80 | 0 | 0 | 29 |
| 47 | Коньково | 14,8 | 15 | 35,00 | 10,00 | 19,60 | 1 | 0 | 37 |
| 48 | Коньково | 14,8 | 3 | 32,80 | 6,50 | 18,50 | 1 | 0 | 30 |
| 49 | НовЧеремуш. | 10,3 | 10 | 39,00 | 9,00 | 19,00 | 1 | 0 | 45 |
| 50 | Университет | 8,7 | 15 | 49,00 | 9,00 | 20,50 | 0 | 1 | 52 |
| 51 | Фрунзенская | 4 | 3 | 32,00 | 6,20 | 19,00 | 1 | 1 | 53 |
| 52 | Пр.Вернадск. | 11,4 | 10 | 33,00 | 6,50 | 19,00 | 1 | 0 | 32 |
| 53 | Пр.Вернадск. | 11,4 | 15 | 32,30 | 6,00 | 21,90 | 0 | 0 | 28 |
| 54 | Юго-Запад | 13,3 | 10 | 30,00 | 7,00 | 19,80 | 1 | 0 | 34 |
| 55 | Юго-Запад | 13,3 | 10 | 34,00 | 9,00 | 19,00 | 1 | 0 | 42 |
| 56 | Юго-Запад | 13,3 | 7 | 33,00 | 7,00 | 19,00 | 0 | 0 | 33 |
| 57 | Академическая | 7,6 | 10 | 30,00 | 6,00 | 18,30 | 1 | 1 | 28 |
| 58 | Академическая | 7,6 | 15 | 32,00 | 6,00 | 18,00 | 1 | 0 | 30 |
| 59 | Коньково | 14,8 | 5 | 33,10 | 7,50 | 18,00 | 1 | 0 | 32 |
| 60 | Коньково | 14,8 | 2 | 38,00 | 7,50 | 19,00 | 1 | 0 | 41 |
| 61 | Коньково | 14,8 | 7 | 38,00 | 8,60 | 19,00 | 1 | 0 | 43 |
| 62 | Коньково | 14,8 | 5 | 37,30 | 6,50 | 19,00 | 1 | 0 | 31 |
| 63 | Ленинский пр. | 5,7 | 8 | 31,40 | 5,60 | 21,00 | 1 | 0 | 33 |
| 64 | Ленинский пр. | 5,7 | 7 | 52,00 | 10,00 | 34,00 | 1 | 1 | 60 |
| 65 | Нов.Черемуш | 10,3 | 15 | 30,00 | 6,00 | 17,00 | 1 | 1 | 37 |
| 66 | Нов.Черемуш | 10,3 | 5 | 36,00 | 11,00 | 20,00 | 1 | 0 | 41 |
| 67 | Пр.Вернадск. | 11,4 | 5 | 28,00 | 6,70 | 14,40 | 1 | 0 | 35 |
| 68 | Пр.Вернадск. | 11,4 | 10 | 31,40 | 5,20 | 21,30 | 1 | 0 | 33 |
| 69 | Юго-Запад | 13,3 | 5 | 32,00 | 8,00 | 17,00 | 1 | 0 | 37 |
В дальнейшем мы продолжим работу с этим файлом.
Лекция 2.
Алгебра линейной регрессии
3.1. Обозначения и определения
x - n-вектор-строка переменных xj;
a - n-вектор-столбец коэффициентов (параметров) регрессии a j при переменных x;
b - свободный член в уравнении регрессии;
e - ошибки измерения (ошибки уравнения, необъясненные остатки);
x a = b + e - уравнение (линейной) регрессии;
x a = b - гиперплоскость регрессии размерности n - 1;
a, b, e - истинные значения соответствующих величин;
a, b, e - их оценки;
x - j - вектор x без j-й компоненты;
- a - j - вектор a без j-й компоненты;
Xj - N- вектор-столбец наблюдений {xij} за переменной xj (вектор фактических значений переменной);
X - N ´ n-матрица наблюдений {Xj} за переменными x;
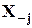 - та же матрица без j-го столбца;
- та же матрица без j-го столбца;
e - N- вектор-столбец ошибок (остатков) по наблюдениям;
X a = 1N b + e - регрессия по наблюдениям (уравнение регрессии);
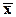
 - n-вектор-строка средних;
- n-вектор-строка средних;
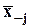 - тот же вектор без j-й компоненты;
- тот же вектор без j-й компоненты;
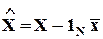 - матрица центрированных наблюдений;
- матрица центрированных наблюдений;
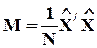 - n ´ n -матрица {mij} оценок ковариаций переменных x (эта матрица, по определению, - вещественная, симметрическая и положительно полуопределенная);
- n ´ n -матрица {mij} оценок ковариаций переменных x (эта матрица, по определению, - вещественная, симметрическая и положительно полуопределенная);
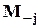 - та же матрица без j- го столбца и j-й строки;
- та же матрица без j- го столбца и j-й строки;
m - j - (n-1)-вектор-столбец (оценок) ковариаций xj c остальными переменными.
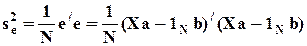 - оценка остаточной дисперсии.
- оценка остаточной дисперсии.
Коэффициенты регрессии a и b находятся так, чтобы 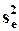 достигала своего наименьшего значения. В этом заключается применение метода наименьших квадратов.
достигала своего наименьшего значения. В этом заключается применение метода наименьших квадратов.
Из условия 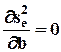 определяется, что
определяется, что  и
и 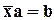 , т.е. гиперплоскость регрессии проходит через точку средних значений переменных, и ее уравнение можно записать в сокращенной форме:
, т.е. гиперплоскость регрессии проходит через точку средних значений переменных, и ее уравнение можно записать в сокращенной форме:
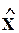 a = e.
a = e.
3.2. Простая регрессия
Когда на вектор параметров регрессии a накладывается ограничение a j=1, имеется в виду простая регрессия, в левой части уравнения которой остается только одна переменная:
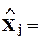
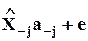
Это уравнение регрессии xj по x - j; переменная xj - объясняемая, изучаемая или моделируемая, переменные x - j - объясняющие, независимые факторы, регрессоры.
Из условия 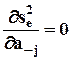 определяется, что
определяется, что  и m - j = M - j a - j. Последнее называется системой нормальных уравнений, из которой находятся искомые МНК-оценки параметров регрессии:
и m - j = M - j a - j. Последнее называется системой нормальных уравнений, из которой находятся искомые МНК-оценки параметров регрессии:
 .
.
Систему нормальных уравнений можно вывести, используя иную логику. Если обе части уравнения регрессии (записанного по наблюденям) умножить слева на 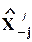 и разделить на N, то получится условие
и разделить на N, то получится условие  , из которого следует искомая система при требованиях
, из которого следует искомая система при требованиях 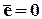 и
и 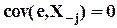 .
.
Такая же логика используется в методе инструментальных переменных. Пусть имеется N ´ (n-1)-матрица наблюдений Z за некоторыми величинами z, называемыми инструментальными переменными, относительно которых известно, что они взаимно независимы с e. Умножение обеих частей уравнения регрессии слева на 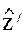 и деление их на N дает условие
и деление их на N дает условие 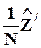
 , из которого - после отбрасывания 2-го члена правой части - следует система нормальных уравнений
, из которого - после отбрасывания 2-го члена правой части - следует система нормальных уравнений
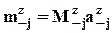
метода инструментальных переменных,
где  .
.
МНК-оценка остаточной дисперсии удовлетворяет следующим формулам:
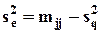 ,
,
где 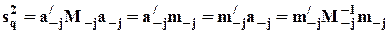 - объясненная дисперсия.
- объясненная дисперсия.
 или
или 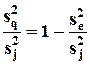 (т.к.
(т.к. 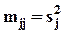 ) - коэффициент детерминации (равный квадрату коэффициента множественной корреляции между xj и x - j), показывающий долю исходной дисперсии моделируемой переменной, которая объяснена регрессионной моделью.
) - коэффициент детерминации (равный квадрату коэффициента множественной корреляции между xj и x - j), показывающий долю исходной дисперсии моделируемой переменной, которая объяснена регрессионной моделью.
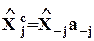 - расчетные значения моделируемой переменной (лежащие на гиперплоскости регрессии).
- расчетные значения моделируемой переменной (лежащие на гиперплоскости регрессии).
В n-пространстве переменных вектора-строки матрицы X образуют так называемое облако наблюдений. Искомая гиперплоскость регрессии в этом пространстве располагается так, чтобы сумма квадратов расcтояний от всех точек облака наблюдений до этой гиперплоскости была минимальна. Данные расcтояния измеряются параллельно оси моделируемой переменной xj.
В N-пространстве наблюдений показываются вектора-столбцы матрицы 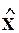 . Коэффициент множественной корреляции между xj и x - j равен косинусу угла между
. Коэффициент множественной корреляции между xj и x - j равен косинусу угла между 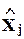 и гиперплоскостью,”натянутой” на столбцы матрицы
и гиперплоскостью,”натянутой” на столбцы матрицы 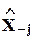 , вектор e является нормалью из
, вектор e является нормалью из 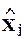 на эту гиперплоскость, а вектор a - j образован коэффициентами разложения проекции
на эту гиперплоскость, а вектор a - j образован коэффициентами разложения проекции 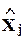 на эту гиперплоскость по векторам-столбцам матрицы
на эту гиперплоскость по векторам-столбцам матрицы 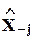 .
.
В зависимости от того, какая переменная остается в левой части уравнения регрессии, получаются различные оценки вектора a (и, соответственно, коэффициента b). Пусть a( j ) - оценка этого вектора из регрессии xj по x - j. Равенство
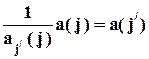
при 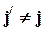 выполняется в том и только в том случае, если e = 0 и, соответственно, R2 = 1.
выполняется в том и только в том случае, если e = 0 и, соответственно, R2 = 1.
При n = 2 регрессия x1 по x2 называется прямой, регрессия x2 по x1 - обратной.
Замечание: в отечественной литературе простой обычно называют регрессию с одной переменной в правой части, а регрессию с несколькими независимыми факторами - множественной.
3.3. Ортогональная регрессия
В случае, когда ограничения на параметры a состоят в требовании равенства единице длины этого вектора
a / a = 1,
получается ортогональная регрессия, в которой расстояния от точек облака наблюдений до гиперплоскости регрессии измеряются перпендикулярно этой гиперплоскости.
Уравнение ортогональной регрессии имеет вид:
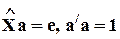 .
.
Теперь применение МНК означает минимизацию 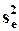 по a при указанном ограничении на длину этого вектора. Из условия равенства нулю производной по a соответствующей функции Лагранжа следует, что
по a при указанном ограничении на длину этого вектора. Из условия равенства нулю производной по a соответствующей функции Лагранжа следует, что
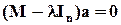 причем
причем 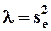 ,
,
(l - половина множителя Лагранжа указанного ограничения) т.е. применение МНК сводится к поиску минимального собственного числа l ковариационной матрицы M и соответствующего ему собственного (правого) вектора a. Благодаря свойствам данной матрицы, искомые величины существуют, они вещественны, а собственное число неотрицательно (предполагается, что оно единственно). Пусть эти оценки получены.
В ортогональной регрессии все переменные x выступают изучаемыми или моделируемыми, их расчетные значения определяются по формуле
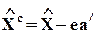 ,
,
а аналогом коэффициента детерминации выступает величина
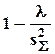 ,
,
где 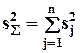 - суммарная дисперсия переменных x, равная следу матрицы M.
- суммарная дисперсия переменных x, равная следу матрицы M.
Таким образом, к n оценкам вектора a простой регрессии добавляется оценка этого вектора ортогональной регрессии, и общее количество этих оценок становится равным n+1.
Задачу простой и ортогональной регрессии можно записать в единой, обобщенной форме:
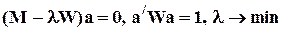 ,
,
где W - диагональная n ´ n-матрица, на диагонали которой могут стоять 0 или 1.
В случае, если в матрице W имеется единственный ненулевой элемент wjj = 1, это - задача простой регрессии xj по xj; если W является единичной матрицей, то это - задача ортогональной регрессии. Очевидно, что возможны и все промежуточные случаи, и общее количество оценок регрессии - 2n - 1.
Задача ортогональной регрессии легко обобщается на случай нескольких уравнений и альтернативного представления расчетных значений изучаемых переменных.
Матрица M, являясь вещественной, симметрической и положительно полуопределенной, имеет n вещественных неотрицательных собственных чисел, сумма которых равна 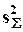 , и n соответствующих им вещественных взаимноортогональных собственных векторов, дающих ортонормированный базис в пространстве наблюдений. Пусть собственные числа, упорядоченные по возрастанию, образуют диагональную матрицу L, а соответствующие им собственные вектора (столбцы) - матрицу A. Тогда
, и n соответствующих им вещественных взаимноортогональных собственных векторов, дающих ортонормированный базис в пространстве наблюдений. Пусть собственные числа, упорядоченные по возрастанию, образуют диагональную матрицу L, а соответствующие им собственные вектора (столбцы) - матрицу A. Тогда
A/A = In, MA = A L.
Собственные вектора, если их рассматривать по убыванию соответствующих им собственных чисел, есть главные компоненты облака наблюдений, которые показывают направления наибольшей “вытянутости” (наибольшей дисперсии) этого облака. Количественную оценку степени этой “вытянутости” (дисперсии) дают соответствующие им собственные числа.
Пусть первые k собственных чисел “малы”.
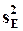 - сумма этих собственных чисел;
- сумма этих собственных чисел;
AE - часть матрицы A, соответствующая им (ее первые k стоблцов); это - коэффициенты по k уравнениям регрессии или k младших главных компонент;
AF - остальная часть матрицы A, это - n - k старших главных компонент или собственно главных компоненет;
A = [AE,AF];
xAE = 0 - гиперплоскость ортогональной регрессии размерности n - k;
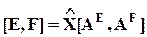 - координаты облака наблюдений в базисе главных компонент;
- координаты облака наблюдений в базисе главных компонент;
E - N ´ k-матрица остатков по уравнениям регрессии;
F - N ´ (n - k)-матрица, столбцы которой есть так называемые главные факторы.
Поскольку A/ = A-1 и AA/ = In, можно записать
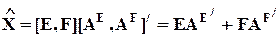 .
.
Откуда получается два возможных представления расчетных значений переменных:
 .
.
Первое из них - по уравнениям ортогональной регрессии, второе (альтернативное) - по главным факторам.
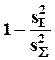 - аналог коэффициента детерминации, дающий оценку “качества” этих обеих моделей.
- аналог коэффициента детерминации, дающий оценку “качества” этих обеих моделей.
3.4. Многообразие оценок регрессии
Множество оценок регрессии не исчерпывается 2n - 1 отмеченными выше элементами.
D - N/ ´ N-матрица преобразований в пространстве наблюдений ( 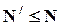 ).
).
Преобразование в пространстве наблюдений проводится умножением слева обеих частей уравнения регрессии (записанного по наблюдениям) на эту матрицу:
 .
.
После такого преобразования - если D не единичная матрица - применение МНК приводит к новым оценкам регрессии (как простой, так и ортогональной), при этом параметр b - если 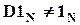 - теряет смысл свободного члена в уравнении.
- теряет смысл свободного члена в уравнении.
C - невырожденная n ´ n-матрица преобразований в пространстве переменных.
Преобразование в пространстве пременных проводится следующим образом: 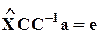 ,
,
и в результате получается новое выражение для уравнения регрессии:
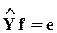 ,
,
где 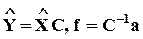 .
.
МНК-оценки f и a количественно различаются, если C не единичная матрица. Однако f является новой оценкой, только если 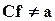 . В противном случае она совпадает с исходной оценкой a с точностью до сделанного преобразования (представляет ту же оценку в другой метрике или шкале измерения).
. В противном случае она совпадает с исходной оценкой a с точностью до сделанного преобразования (представляет ту же оценку в другой метрике или шкале измерения).
Результаты преобразования в пространстве переменных различны для простой и ортогональной регрессии.
В случае простой регрессии xj по x - j это преобразование не приводит к получению новых оценок, если j-я строка матрицы C является ортом, т.е. в независимые факторы правой части не “попадает” - после преобразования - моделируемая переменная. Если C диагональная матрица с элементами cjj=1, 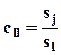 при
при 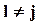 , то оценка f дается в так называемой стандартизированной шкале.
, то оценка f дается в так называемой стандартизированной шкале.
Если j-я строка матрицы C имеет ненулевые внедиагональные элементы, Cf и a совпадают только при R2 = 1.
В случае ортогональной регрессии задача определения f записывается следующим образом:
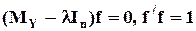 ,
,
где 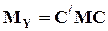 .
.
После обратной подстановки переменных и элементарного преобразования она приобретает следующий вид:
 ,
,
где 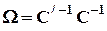 .
.
Решение этой задачи дает новую оценку, даже если C является диагональной матрицей. Это - так называемая регрессия в метрике W -1.
Основная модель линейной регрессии
4.1. Различные формы уравнения регрессии
x - моделируемая переменная;
z - n-вектор-строка независимых факторов;
x = z a + b + e - уравнение регрессии;
X, Z - N-вектор и N ´ n-матрица наблюдений за соответствующими переменными;
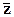 - n-вектор-строка средних значений переменных z.
- n-вектор-строка средних значений переменных z.
Первые две формы уравнения регрессии по наблюдениям аналогичны используемым в предыдущем разделе и имеют следующий вид:
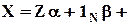 e,
e,
или 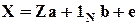 (истинные значения заменены их оценками)
(истинные значения заменены их оценками)
- исходная форма;
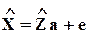
- сокращенная форма.
Оператор МНК-оценивания для этих двух форм имеет следующий вид:
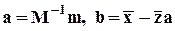 ,
,
где 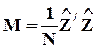 - nxn-матрица ковариации (вторых центральных моментов) z;
- nxn-матрица ковариации (вторых центральных моментов) z;
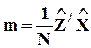 - n-вектор-столбец ковариации между z и x.
- n-вектор-столбец ковариации между z и x.
Третья форма - без свободного члена - записывается следующим образом:
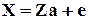 ,
,
где Z - N ´ (n+1)-матрица, последний столбец которой состоит из единиц (равен 1N);
a - (n+1)-вектор-столбец, последний элемент которого является свободным членом регрессии.
Какая из этих форм регрессии используется и, соответственно, что именно означают a и Z, будет в дальнейшем ясно из контекста или будет специально поясняться.
В этом разделе, в основном, используется форма уравнения регрессии без свободного члена.
Оператор МНК-оценивания для нее записывается более компактно:
 ,
,
но 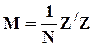 - (n+1) ´ (n+1)-матрица вторых начальных моментов [z,1];
- (n+1) ´ (n+1)-матрица вторых начальных моментов [z,1];
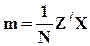 - (n+1)-вектор-столбец вторых начальных моментов между [z,1] и x.
- (n+1)-вектор-столбец вторых начальных моментов между [z,1] и x.
Если в этом операторе вернуться к обозначениям первых двух форм уравнения регрессии, то получится следующее выражение:
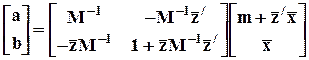 ,
,
из которого видно, что
- обратная матрица ковариации z (размерности N ´ N) совпадает с соответствующим блоком обратной матрицы вторых начальных моментов (размерности (N+1) ´ (N+1));
- результаты применения двух приведенных операторов оценивания одинаковы.
4.2. Основные гипотезы, свойства оценок
1. Между переменными x и z существует зависимость x = z a + b + e.
2. Переменные z детерминированы, наблюдаются без ошибок и линейно независимы (в алгебраическом смысле).
3. E( e ) = 0, E( ee / ) = s 2 IN.
4. В модели линейной регрессии математической статистики, в которой переменные z случайны, предполагается, что ошибки e не зависят от них и - по крайней мере - не скоррелированы с ними. В данном случае это предположение формулируется так: независимо от того, какие значения принимают переменные z, ошибки e удовлетворяют гипотезе 3.
В этих предположениях a относится к классу линейных оценок, т.к.
a = LX,
где L = 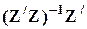 - неслучайный (n+1) ´ (N+1)-оператор оценивания;
- неслучайный (n+1) ´ (N+1)-оператор оценивания;
а также доказывается что
- a является несмещенной оценкой a, их матрица ковариации Ma равна 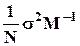 (в обозначениях сокращенной формы уравнения регрессии это выражение давало бы - как показано в предыдущем пункте - матрицу ковариации коэффициентов регрессии при независимых факторах, а дисперсия свободного члена определялась бы по формуле
(в обозначениях сокращенной формы уравнения регрессии это выражение давало бы - как показано в предыдущем пункте - матрицу ковариации коэффициентов регрессии при независимых факторах, а дисперсия свободного члена определялась бы по формуле  ), и дисперсия любой их линейной комбинации минимальна на множестве линейных оценок, т.е. они относятся к классу BLUE - Best Linear Unbiased Estimators;
), и дисперсия любой их линейной комбинации минимальна на множестве линейных оценок, т.е. они относятся к классу BLUE - Best Linear Unbiased Estimators;
- несмещенной оценкой s 2 является
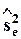 =
= 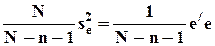 .
.
Для расчета коэффициента детерминации можно использовать следующую формулу:
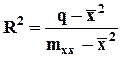 ,
,
где  ,
,
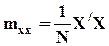 .
.
Если предположить, что e (и, следовательно, их оценки e) распределены нормально:
e 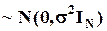 ,
,
то оценки a также будут иметь нормальное распределение:
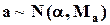 ,
,
они совпадут с оценками максимального правдоподобия, будут несмещенными, состоятельными и эффективными.
В этом случае можно строить доверительные интервалы для оценок и использовать статистические критерии проверки гипотез.
(1- q )100-процентный доверительный интервал для a i , i =1,...,n+1 (a n+1=b), строится следующим образом:
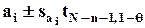 ,
,
где 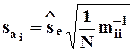 - среднеквадратическое отклонение ai (
- среднеквадратическое отклонение ai ( 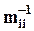 - ii-й элемент матрицы M - 1);
- ii-й элемент матрицы M - 1);
tN-n-1,1- q - (1- q )100-процентный двусторонний квантиль tN-n-1-распределения.
Для проверки нулевой гипотезы a i = 0 применяется t-критерий. Гипотеза отвергается (влияние i-го фактора считается статистически значимым) с вероятностью ошибки (1-го рода) q, если
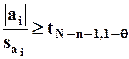 ,
,
т.к. при выполнении нулевой гипотезы величина 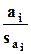 имеет tN-n-1-распределение. Эта величина называется t-статистикой (ti-статистикой) и ее фактическое значение обозначается в дальнейшем
имеет tN-n-1-распределение. Эта величина называется t-статистикой (ti-статистикой) и ее фактическое значение обозначается в дальнейшем 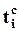 .
.
При использовании современных статистических пакетов программ не требуется искать нужные квантили t-распределения в статистических таблицах, поскольку в них (пакетах) рассчитывается уровеньошибки  , с которой можно отвергнуть нулевую гипотезу, т.е. такой, что:
, с которой можно отвергнуть нулевую гипотезу, т.е. такой, что:
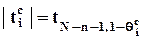 ,
,
и, если он меньше желаемого значения либо равен ему, то нулевая гипотеза отвергается.
Для проверки нулевой гипотезы об отсутствии искомой связи 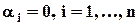 применяется F-критерий. Если эта гипотеза верна, величина
применяется F-критерий. Если эта гипотеза верна, величина
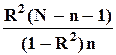
имеет Fn,N-n-1-распределение. Данная величина называется F-статистикой и ее фактическое значение обозначается в дальнейшем Fc. Нулевая гипотеза отвергается (влияние z на x считается статистически значимым) с вероятностью ошибки (1-го рода) q, если
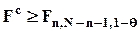 ,
,
где Fn,N-n-1,1- q - (1- q )100-процентный (односторонний) квантиль Fn,N-n-1-распределения.
В современных статистических пакетах программ также рассчитывается уровень q с ошибки для Fc, такой, что
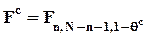 .
.
Уместно отметить, что приведенные в разделе 2.1. сведения являются частным случаем рассмотренных здесь результатов при n=0.
4.3. Независимые факторы
Если не выполняется 2-я гипотеза, и некоторые из переменных z линейно зависят от других, то матрица M вырождена, и использование приведенного оператора оценивания невозможно.
Вообще говоря, предложить метод оценивания параметров регрессии в этом случае можно. Так, пусть множество независимых факторов разбито на две части (в этом фрагменте используются обозначения сокращенной формы уравнения регрессии):
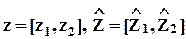 ,
, 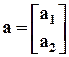 ,
,
и 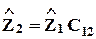 .
.
Тогда можно записать уравнение регрессии в форме
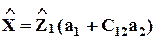 + e,
+ e,
и оценить линейную комбинацию параметров 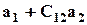 (предполагая, что столбцы Z1 линейно независимы). Но чтобы оценить сами параметры, нужна априорная информация, например:
(предполагая, что столбцы Z1 линейно независимы). Но чтобы оценить сами параметры, нужна априорная информация, например: 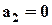 .
.
Однако вводить в регрессию факторы, которые линейно зависят от уже введенных факторов, не имеет смысла, т.к. при этом не растет объясненная дисперсия (см. ниже).
На практике редко встречается ситуация, когда матрица M вырождена. Более распространен случай, когда она плохо обусловлена (между переменными Z существуют зависимости близкие к линейным). В этом случае имеет место мультиколлинеарность факторов. Поскольку гипотеза 2 в части отсутствия ошибок измерения, как правило, нарушается, получаемые (при мультиколлинеарности) оценки в значительной степени обусловлены этими ошибками измерения. В таком случае (если связь существует), обычно, факторы по отдельности оказываются незначимыми по t-критерию, а все вместе - существенными по F-критерию. Поэтому в регрессию стараются не вводить факторы сильно скоррелированные с остальными.
В общем случае доказывается, что
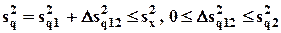 ,
,
где 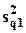 и
и 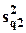 - дисперсии, объясненные факторами z1 и z2 по отдельности;
- дисперсии, объясненные факторами z1 и z2 по отдельности;
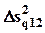 - прирост объясненной дисперсии, вызванный добавлением в регрессии факторов z2 к факторам z1.
- прирост объясненной дисперсии, вызванный добавлением в регрессии факторов z2 к факторам z1.
В соотношении для прироста объясненной дисперсии:
- левая часть выполняется как строгое равенство, если и только если
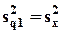 (коэффициент детерминации в регрессии по z1 уже равен единице), или
(коэффициент детерминации в регрессии по z1 уже равен единице), или
вектор остатков в регрессии по z1 ортогонален факторам 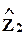 , т.е. имеет с ними нулевую корреляцию (возможное влияние факторов z2 уже “приняли” на себя факторы z1), или
, т.е. имеет с ними нулевую корреляцию (возможное влияние факторов z2 уже “приняли” на себя факторы z1), или
факторы 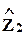 линейно зависят от факторов
линейно зависят от факторов 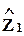 ;
;
- правая часть выполняется как строгое равенство, если и только если
факторы 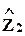 ортогональны факторам
ортогональны факторам 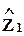 .
.
Если в множество линейно независимых факторов добавлять новые элементы, то коэффициент детерминации растет вплоть до единицы, после чего рост прекращается. Своего максимального значения он обязательно достигнет при n = N (возможно и раньше) - даже если вводимые факторы не влияют по-существу на изучаемую переменную. Поэтому сам по себе коэффициент детерминации не может служить статистическим критерием “качества” уравнения регрессии. Более приемлем в этой роли коэффициент детерминации, скорректированный на число степеней свободы:
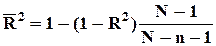 ,
,
который может и уменьшиться при введении нового фактора. Точную же статистическую оценку качества (в случае нормальности распределения остатков) дает F-критерий. Однако учитывая, что значения Fc оказываются несопоставимыми при изменении n (т.к. получают разное число степеней свободы), наиболее правильно эту роль возложить на уровень ошибки q с для Fc.
В результате введения новых факторов в общем случае меняются оценки параметров при ранее введенных факторах:
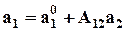 ,
,
где 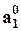 - оценка параметров регрессии по z1 (до введения новых факторов);
- оценка параметров регрессии по z1 (до введения новых факторов);
A12 - матрица, столбцы которой являются оценками параметров регрессии переменных z2 по z1.
“Старые” оценки параметров сохраняются ( 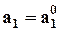 ), если и только если
), если и только если
- коэффициент детерминации в регрессии по z1 уже равен единице, или
вектор остатков в регрессии по z1 ортогонален факторам 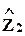 (в этих двух случаях a2 = 0), или
(в этих двух случаях a2 = 0), или
факторы 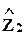 ортогональны факторам
ортогональны факторам 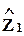 (в этом случае A12 = 0).
(в этом случае A12 = 0).
Итак, возникает проблема определения истинного набора факторов, фигурирующих в гипотезе 1, который позволил бы найти оценки истинных параметров регрессии. Определение такого набора факторов есть спецификация модели. Формальный подход к решению этой проблемы заключается в поиске так называемого наилучшего уравнения регрессии, для чего используется процесс (метод) шаговой регрессии.
Пусть z - полный набор факторов, потенциально влияющих на x. Рассматривается процесс обращения матрицы ковариации переменных [x,z]. В паре матриц (n+1) ´ (n+1)
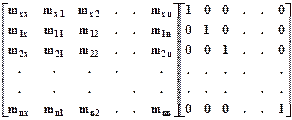
делаются одновременные преобразования их строк в орты. Известно, что, если 1-ю матрицу преобразовать в единичную, то на месте 2-й матрицы будет получена обратная к 1-й (исходной). Пусть этот процесс не завершен, и только несколько строк 1-й матрицы (но не ее 1-я строка) преобразованы в орты. Это - ситуация на текущем шаге процесса.
На этом шаге строкам-ортам в 1-й матрице соответствуют включенные в регрессию факторы, на их месте в 1-й строке этой матрицы оказываются текущие оценки параметров регрессии при них. Строкам-ортам во 2-й матрице соответствуют невведенные факторы, на их месте в 1-й строке 1-й матрицы размещаются коэффициенты ковариации этих факторов с текущими остатками изучаемой переменной. На месте mxx показывается текущее значение остаточной дисперсии.
На каждом шаге оцениваются последствия введения в регрессию каждого не включенного фактора (преобразованием в орты сответствующих строк 1-й матрицы) и исключения каждого введенного ранее фактора (преобразованием в орты соответствующих строк 2-й матрицы). Выбирается тот вариант, который дает минимальный уровень ошибки q с для Fc. Процесс продолжается до тех пор, пока этот уровень сокращается.
Иногда в этом процессе используются более простые критерии. Например, задается определенный уровень t-статистики (правильнее - уровень ошибки q с для tc), и фактор вводится в уравнение, если фактическое значение tc для него выше заданного уровня (ошибка q с ниже ее заданного уровня), фактор исключается из уравнения в противном случае.
Такие процессы, как правило, исключают возможность введения в уравнение сильно скоррелированных факторов, т.е. решают проблему мультиколлинеарности.
Формальные подходы к спецификации модели должны сочетаться с теоретическими подходами, когда набор факторов и, часто, знаки параметров регрессии определяются из теории изучаемого явления.
4.4. Прогнозирование
Требуется определить наиболее приемлемое значения для xN+1 (прогноз), если известны значения независимых факторов (вектор-строка):
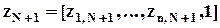 .
.
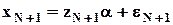 - истинное значение искомой величины;
- истинное значение искомой величины;
 - ожидаемое значение;
- ожидаемое значение;
 - искомый МНК-прогноз.
- искомый МНК-прогноз.
Полученный прогноз не смещен относительно ожидаемого значения:
 ,
,
и его ошибка 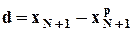 имеет нулевое матожидание:
имеет нулевое матожидание:
E(d) = 0,
и дисперсию 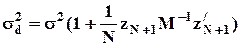 , которая минимальна в классе линейных оценок a.
, которая минимальна в классе линейных оценок a.
Оценка стандартной ошибки прогноза при n = 1 рассчитывается по формуле
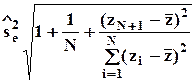 .
.
Дата добавления: 2019-11-25; просмотров: 173; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
