Гетероскедастичность и автокорреляция ошибок

5.1. Обобщенный метод наименьших квадратов (взвешенная регрессия)

Если матрица ковариации ошибок по наблюдениям отлична от s ² I_N (нарушена 3-я гипотеза основной модели), то МНК-оценки параметров регрессии остаются несмещенными, но перестают быть эффективными в классе линейных. Смещенными оказываются МНК-оценки их ковариции, в частности оценки их стандартных ошибок (как правило, они преуменьшаются).

Пусть теперь E( ee ^/ ) = s ² W, где W - вещественная, симметрическая положительно определенная матрица (структура ковариации ошибок). Обобщенный метод наименьших квадратов (ОМНК), приводящий к оценкам класса BLUE, означает минимизацию взвешенной суммы квадратов отклонений:

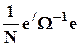Для доказательства проводится преобразование в пространстве наблюдений с помощью невырожденной N ´ N-матрицы D, такой, что . После такого преобразования остатки D e начинают удовлетворять 2-й гипотезе.

На практике с матрицами W общего вида обычно не работают. Рассматривается два частных случая.

5.2. Гетероскедастичность ошибок

Пусть ошибки не скоррелированы по наблюдениям, и матрица W диагональна. Если эта матрица единична, т.е. дисперсии ошибок одинаковы по наблюдениям (гипотеза 3 не нарушена), то имеет место гомоскедастичность или однородность ошибок по дисперсии. В противном случае констатируют гетероскедастичность ошибок или их неоднородность по дисперсии.

Для проверки гипотезы о гомоскедастичности можно использовать критерий Бартлета. Для расчета b^c - статистики, лежащей в основе применения этого критерия, множество МНК-оценок остатков e_i, i = 1,...,N делится на k непересекающихся подмножеств.

N_l - количество элементов в l-м подмножестве, ;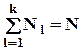

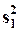- оценка дисперсии в l-м подмножестве;

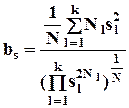- отношение средней арифметической дисперсий к средней геометрической; это отношение больше или равно единице, и чем сильнее различаются дисперсии по подмножествам, тем оно выше;

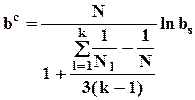При однородности наблюдений по дисперсии эта статистика распределена как .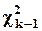

Факт неоднородности наблюдений по дисперсии остатков мало сказывается на качестве оценок регрессии, если эти дисперсии не скоррелированы с независимыми факторами. Проверить наличие зависимости дисперсии ошибок от факторов-регрессоров можно следующим образом.

Все наблюдения упорядочиваются по возрастанию одного из независимых факторов или расчетного значения изучаемой переменной Za. Оценивается остаточная дисперсия 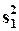по K “малым” и 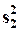по K “большим” наблюдениям (“средние” N - 2K наблюдения в расчете не участвуют, а K выбирается приблизительно равным трети N). В случае гомоскедастичности ошибок отношение 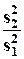распределено как F_K-n-1,K-n-1.

Если гипотеза гомоскедастичности отвергается, необходимо дать оценку матрице W. Совместить проверку этой гипотезы с оценкой данной матрицы можно следующим образом.

В качестве оценок дисперсии ошибок по наблюдениям принимаются квадраты оценок остатков 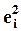, и строится регрессия 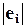на все множество независимых факторов или какое-то их подмножество. Если какая-то из этих регрессий оказывается статистически значимой, то гипотеза гомоскедастичности отвергается, и в качестве оценок 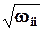( по предположению) примаются расчетные значения .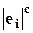

В некоторых статистических критериях проверки на гомоскедастичность в качестве оценок w _ii принимаются непосредственно .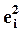

Имея оценку матрицы W, можно провести преобразование в пространстве наблюдений с помощью матрицы 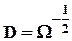, после которого остатки D e можно считать удовлетворяющими гипотезе 3.

5.3. Автокорреляция ошибок

Пусть теперь наблюдения однородны по дисперсии и их последовательность имеет физический смысл и жестко фиксирована (например, наблюдения проводятся в последовательные моменты времени).

Для проверки гипотезы о наличии линейной автокорреляции 1-го порядка ошибок по наблюдениям

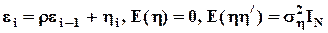где r - коэффициент авторегрессии 1-го порядка;

h - N-вектор-столбец { h _i };

можно использовать критерий Дарбина-Уотсона или DW-критерий (при автокорреляции 2-го и более высоких порядков его применение становится ненадежным).

Фактическое значение d^c статистики Дарбина-Уотсона (отношения Фон-Неймана) или DW-статистики раcсчитывается следующим образом:

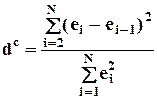
Оно лежит в интервале от 0 до 4, в случае отсутствия автокорреляции ошибок приблизительно равно 2, при положительной автокорреляции смещается в меньшую сторону, при отрицательной - в большую сторону.

Если r = 0, величина d распределена нормально, но параметры этого распределения зависят не только от N и n. Поэтому существует по два значения для каждого (двустороннего) квантиля, соответствующего определенным q, N и n: его нижняя d_L и верхняя d_U границы. Нулевая гипотеза принимается, если 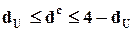; она отвегается в пользу гипотезы о положительной автокорреляции, если 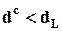, и в пользу гипотезы об отрицательной автокорреляции, если 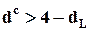. Если или 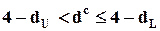, вопрос остается открытым (это - зона неопределенности DW-критерия).

Пусть нулевая гипотеза отвергнута. Тогда необходимо дать оценку матрицы W.

Оценка r параметра авторегрессии r определяется из приближенного равенства

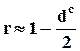или рассчитывается непосредственно из регрессии e на него самого со двигом на одно наблюдение.

Оценкой матрицы W является 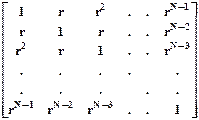, а матрица D

преобразований в пространстве наблюдений равна .

Для преобразования в простанстве наблюдений, называемом в данном случае авторегрессионным, используют обычно указанную матрицу без 1-й строки, что ведет к сокращению количества наблюдений на одно. В результате такого преобразования из каждого наблюдения, начиная со 2-го, вычитается предыдущее, умноженное на r, теоретическими остатками становятся h _i, которые удовлетворяют гипотезе 2.

После этого преобразования снова оцениваются параметры регрессии. Если новое значение DW-статистики неудовлетворительно, то можно провести следующее авторегрессионное преобразование.

Обобщает процедуру последовательных авторегрессионных преобразований метод Кочрена-Оркарта, который заключается в следующем.

Для одновременной оценки r, a и b используется критерий ОМНК (в обозначениях исходной формы уравнения регрессии):

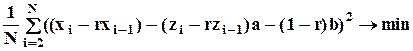где z_i - n-вектор-строка значений независимых факторов в i-м наблюдении (i-строка матрицы Z).

Поскольку производные функционала по искомым величинам нелинены относительно них, применяется итеративная процедура, на каждом шаге которой сначала оцениваются a и b при фиксированном значении r предыдущего шага (на первом шаге обычно r = 0), а затем - r при полученных значениях a и b. Процесс, как правило, сходится.

Дата добавления: 2019-11-25; просмотров: 217; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 Следующая ⇒

Мы поможем в написании ваших работ!