Элементы математической статистики

1. Проработать текст лекции, ответить на вопросы для самопроверки

(с. 51 вопросы 1 – 27)

Тема лекции 3.1 Статистическое распределение выборки. Эмпирическая функция распределения

Тема лекции 3.2 Статистические оценки параметров распределения

Тема лекции 3.3 Доверительные интервалы для оценки математического ожидания и среднеквадратического отклонения нормального распределения

Рассмотреть примеры решения задач

3. Решить задачи для самостоятельной работы и подготовиться к практической работе № 9 по теме «Эмпирические функции. Вычисление выборочных средней и дисперсии. Построение доверительных интервалов»

Выполнение семестрового задания (с. 57)

Примеры решения задач

Пример 1. Построить эмпирическую функцию по данному распределению выборки:

варианты x_i 2 6 10

частоты n_i 12 18 30

Решение. Найдем объем выборки: 12 + 18 + 30 = 60. Наименьшая варианта равна 2, следовательно,

F*(x) = 0 при х ≤ 2.

Значение X < 6, а именно x₁ = 2, наблюдалось 12 раз, следовательно, F*(x)=12/60 =0,2 при 2 < x ≤ 6.

Значения X < 10, а именно х₁ = 2 и х₂ = 6, наблюдались 12 + 18 = 30 раз, следовательно, F* (х) = 30/60 = 0,5 при 6 < х ≤ 10. Так как x = 10 — наибольшая варианта, то F*(x)= 1 при х > 10.

Искомая эмпирическая функция

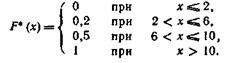
График этой функции изображен на рисунке

Пример 2. Случайная величина X имеет нормальное распределение с известным средним квадратическим отклонением σ = 3. Найти доверительные интервалы для оценки неизвестного математического ожидания а по выборочным средним 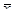, если объем выборки

n= 36 и задана надежность оценки γ = 0,95.

Решение. Найдем t. Из соотношения 2∙Ф( t ) = 0,95 получим Ф( t ) = 0,475. По таблице значений функции Лапласа находим t = 1,96.

Найдем точность оценки:

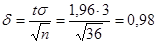
Доверительный интервал таков: ( 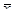— 0,98; 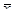+0,98). Например, если 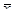= 4,1, то доверительный интервал имеет следующие доверительные границы:

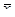— 0,98 = 4,1 — 0,98 = 3,12; 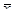+ 0,98 = 4,1+ 0,98 = 5,08.

Таким образом, значения неизвестного параметра а, согласующиеся с данными выборки, удовлетворяют неравенству 3,12 < а < 5,08.

Пример 3. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n =16 найдены выборочная средняя 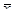= 20,2 и «исправленное» среднее квадратическое отклонение s = 0,8. Оценить неизвестное математическое ожидание при помощи доверительного интервала с надежностью 0,95.

Решение. Найдем t_γ. Пользуясь таблицей приложения 3, по γ = 0,95 и n=16 находим t_γ=2,13.

Найдем доверительные границы:

20,2 — 2,13 ∙ 0,8/ =19,774

20,2 + 2,13 ∙ 0,8/ = 20,626.

Итак, с надежностью 0,95 неизвестный параметр а заключен в доверительном интервале 19,774 < а < 20,626.

Пример 4. Количественный признак X генеральной совокупности распределен нормально. По выборке объема n = 25 найдено «исправленное» среднее квадратическое отклонение s=0,8. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение σ с надежностью 0,95.

Решение. По таблице приложения 4 по данным γ = 0,95 и n = 25 найдем q = 0,32.

Искомый доверительный интервал таков:

0,8 (1—0,32) < а < 0,8 (1+0,32), или 0,544 < а < 1,056.

Решение. По таблице приложения 4 по данным γ = 0,95 и n = 25 найдем q = 0,32.

Искомый доверительный интервал таков:

0,8 (1—0,32) < а < 0,8 (1+0,32), или 0,544 < а < 1,056.

Дата добавления: 2019-09-13; просмотров: 280; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 4 5 6 7 8 91011 12 13 Следующая ⇒

Мы поможем в написании ваших работ!