Полученное уравнение называется уравнением прямой, проходящей через данную точку с заданным угловым коэффициентом.
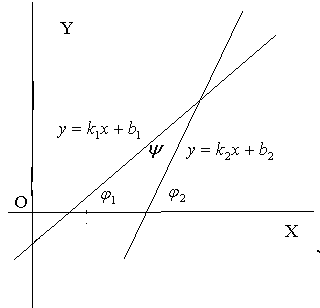
Пусть даны две прямые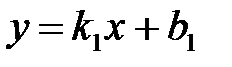 
, 
. Обозначим 
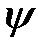- угол между ними. Пусть 
, 
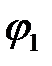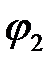углы наклона к оси Х соответствующих прямых
Тогда =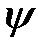 
, 
.
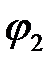
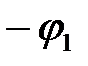Тогда условие параллельности прямых имеет вид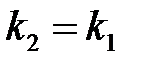 
, а условие перпендикулярности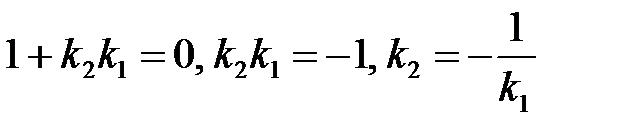 
В заключение рассмотрим две задачи.
Задача. Вершины треугольника АВС имеют координаты: A(4;2), B(10;10), C(20;14).
Найти: а) уравнение и длину медианы, проведенной из вершины А;
б) уравнение и длину высоты, проведенной из вершины А;
в) уравнение биссектрисы, проведенной из вершины А;
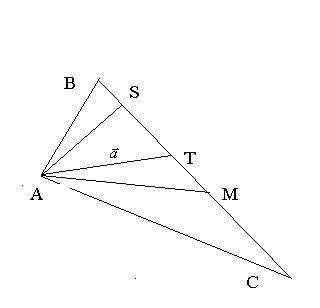
Определим уравнение медианы АМ.
Точка М(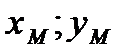 
) середина отрезка ВС.
Тогда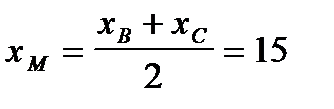 
, 
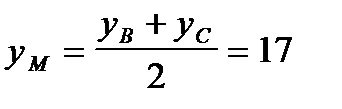. Следовательно, точка М имеет координаты M(15;17). Уравнение медианы на языке аналитической геометрии это уравнение прямой, проходящей через точку А(4;2) параллельно вектору 
={11;15}. Тогда уравнение медианы имеет вид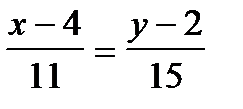 
. Длина медианы АМ= 
.
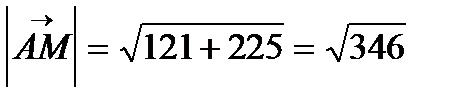Уравнение высоты AS - это уравнение прямой, проходящей через точку А(4;2) перпендикулярно вектору 
={10;4}. Тогда уравнение высоты имеет вид 10(x-4)+4(y-2)=0, 5x+2y-24=0.
Длина высоты - это расстояние от точки А(4;2) до прямой ВС. Данная прямая проходит через точку B(10;10) параллельно вектору ={10;4}. Ее уравнение имеет вид 
, 2x-5y+30=0. Расстояние AS от точки А(4;2) до прямой ВС, следовательно, равно AS=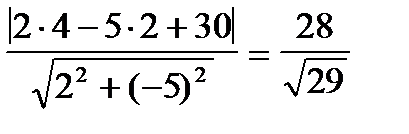 
.
Для определения уравнения биссектрисы найдем вектор 
параллельный этой прямой. Для этого воспользуемся свойством диагонали ромба. Если от точки А отложить единичные векторы одинаково направленные с векторам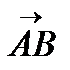и 
и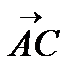 
, то вектор, равный их сумме, будет параллелен биссектрисе. Тогда имеем = 
+ 
.
|
|
|
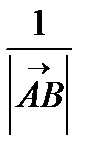
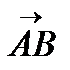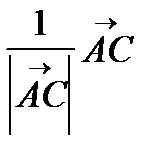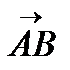={6;8}, 
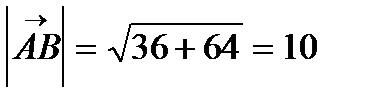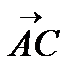, ={16,12}, 
.
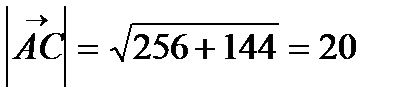Тогда = 
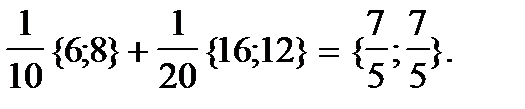В качестве направляющего вектора искомой прямой может служить вектор 
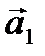={1;1}, коллинеарный данному. Тогда уравнение искомой прямой имеет вид 
или x-y-2=0.
Уравнение окружности
Определение. Общим уравнением линии второго порядка называется уравнение вида
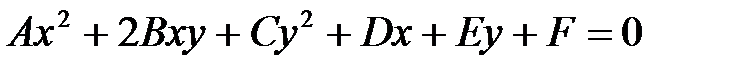, где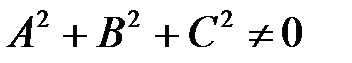 
.
Пусть окружность имеет радиус 
, а ее центр находится в точке 
. Точка 
лежит на окружности тогда и только тогда, когда модуль вектора 
равен , то есть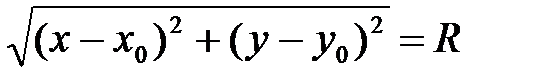 
. Последнее равенство выполнено тогда и только тогда, когда
(1)
Уравнение (1) и является искомым уравнением окружности.
Уравнение сферы
Пусть сфера имеет радиус , а ее центр находится в точке 
. Точка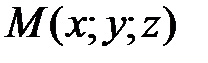 
лежит на сфере тогда и только тогда, когда модуль вектора равен , то есть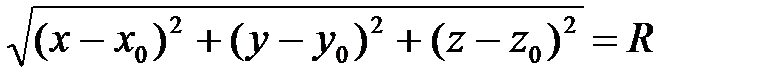 
. А последнее равенство выполнено тогда и только тогда, когда
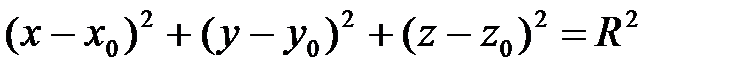(1)
Уравнение (1) и является искомым уравнением сферы.
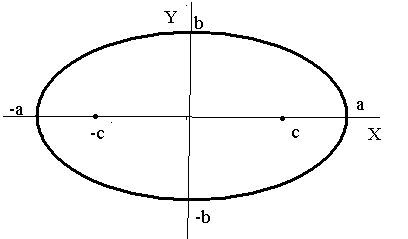
5.3 Эллипс.
Определение. Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами эллипса равна постоянной величине, большей, чем расстояние между фокусами.
|
|
|
Нарисовать эллипс очень просто. Берем нерастяжимую нить, по длине равную сумме расстояний до фокусов. Концы нити закрепляем в фокусах. А далее ведем карандашом вдоль нити, оставляя ее все время натянутой.
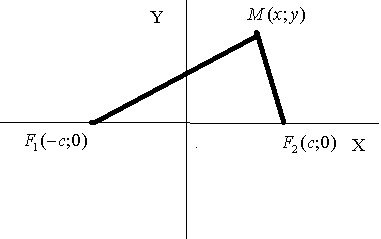
Обозначим расстояние между фокусами 
.
Сумму расстояний до фокусов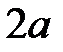 
.
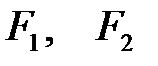- фокусы эллипса имеют координаты. 
.
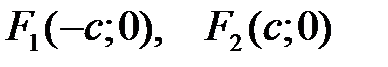Пусть точка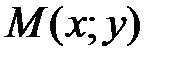 
- лежит на эллипсе.
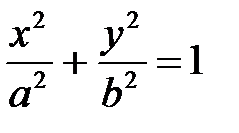- каноническое уравнением эллипса.
Заметим, что в каноническом уравнении обязательно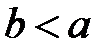 
.
Величины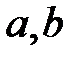 
называются соответственно большая и малая полуоси эллипса. Фокусы эллипса соответственно имеют координаты 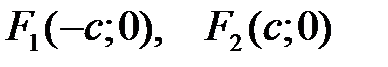, где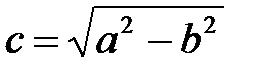 
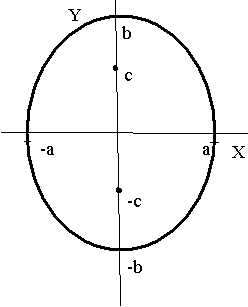
Иногда приходится иметь дело с уравнением вида 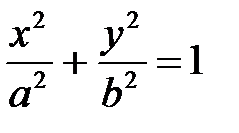, где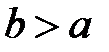 
. Это уравнение так же является уравнением эллипса, но не является каноническим, поскольку фокусы лежат на оси OY. Такой эллипс называется сопряженным.
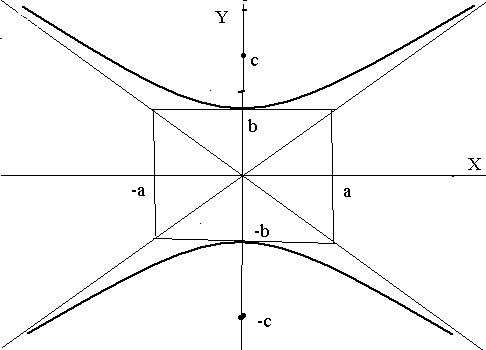
Гипербола
Гиперболой называется геометрическое место точек плоскости, для которых разность расстояний до двух фиксированных точек плоскости, называемых фокусами эллипса равна по абсолютной величине постоянной, меньшей, чем расстояние между фокусами.
|
|
|
Обозначим расстояние между фокусами .
Разность расстояний до фокусов .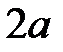
Тогда точки 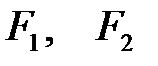- фокусы гиперболы имеют координаты. 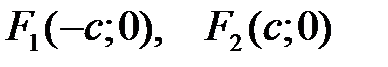. Пусть точка 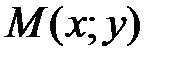- лежит на гиперболе.
- каноническое уравнением гиперболы.
Фокусы гиперболы соответственно имеют координаты 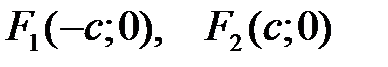, где 
Асимптотами являются прямые 
. Отметим, что эти прямые являются диагоналями прямоугольника, образованного прямыми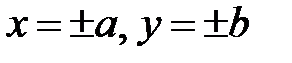 
Иногда приходится иметь дело с уравнением вида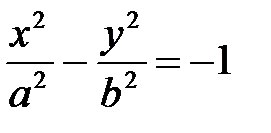 
. Это уравнение так же является уравнением гиперболы, но не является каноническим. Фокусы данной гиперболы лежат на оси Y. Такая гипербола называется сопряженной.
5.5 Парабола.
Определение. Параболой называется геометрическое место точек плоскости, для которых расстояние до фиксированной точки плоскости, называемой фокусом параболы, равно расстоянию до фиксированной прямой, называемой директрисой параболы.
Каноническое уравнение параболы.
Расстояние между фокусом и директрисой обозначим 
. Тогда фокус F имеет координаты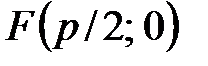 
. Уравнение директрисы имеет вид 
. Пусть точка 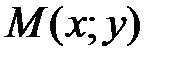лежит на параболе.
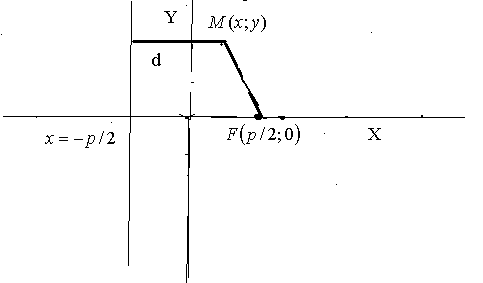
Расстояние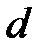 
от этой точки до директрисы равно 
,
Уравнение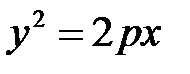 
называется каноническим уравнением параболы.
|
|
|
Точка О с координатами О(0;0) называется вершиной параболы.
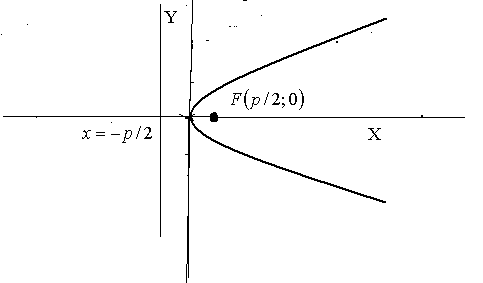
Иногда приходится рассматривать уравнения вида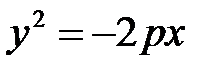 
; 
; 
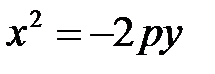. Эти уравнения являются уравнениями параболы, но не являются каноническими.
Дата добавления: 2019-09-13; просмотров: 185; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!