Исследование очередного решения на оптимальность
С помощью метода потенциалов, уменьшающего объём вычислений, легко определить, является ли полученное решение оптимальным. Так для определе-ния оптимальности решения, представленного таблицей 2, каждый тариф сij, находящийся в одной клетке с базисной переменной, выражается в виде суммы потенциалов соответствующей базы αiи заказчика βj. Тогда для найденного плана перевозок образуется система уравнений
с11 = α1 + β1 = 70,
с12 = α1 + β2 = 50,
с13 = α1 + β3 = 15,
с21 = α2 + β1 = 80,
с24 = α2 + β4 = 60,
с34 = α3 + β4 = 11.
Если α1 = 0, то β1 = 70,
α2 = 10, β2 = 50,
α3 = – 39, β3 = 15,
β4 = 50.
При этом значения алгебраической суммы тарифов для свободных клеток таблицы 2 оказываются равными
s14 = c14 – c'14 = c14 – (α1 + β4) = 80 – 50 = 30,
s22 = c22 – c'22 = c22 – (α2 + β2) = 90 – (10 + 50) = 30,
s23 = c23 – c'23 = c23 – (α2 + β3) = 40 – (10 + 15) = 15,
s31 = c31 – c'31 = c31 – (α3 + β1) = 50 – (–39 + 70) = 19,
s32 = c32 – c'32 = c32 – (α3 + β2) = 10 – (–39 + 50) = –1,
s33 = c33 – c'33 = c33 – (α3 + β3) = 90 – (–39 + 15) = 114.
Вычисления показывают, что план перевозок, соответствующий последнему решению, представленному в таблице 2, можно улучшить, производя цикл пересчёта со свободной клеткой (3;2):
Таблица 3
|
Базы | Заказчики | Запасы на базах | |||
| В1 | В2 | В3 | В4 | ||
| А1 | 70 140 | 50 60 | 15 100 | 80 – | 300 т. |
| А2 | 80 30 | 90 – | 40 – | 60 120 | 150 т. |
| А3 | 50 – | 10 50 | 90 – | 11 – | 50 т. |
| Потребности заказчика | 170 т. | 110 т. | 100 т. | 120 т. | 500 т. 500 т. |
|
|
|
Исследование очередного решения на оптимальность продолжается аналогичным образом:
с11 = α1 + β1= 70, с21 = α2 + β1= 80,
с12 = α1 + β2= 50, и с24 = α2 + β4= 60,
с13 = α1 + β3= 15 с32 = α3 + β2= 10.
Тогда, если α1 = 0, то β1= 70,
α2 = 10, β2= 50,
α3 = – 40, β3= 15,
β4= 50.
При этом значения алгебраической суммы тарифов для свободных клеток таблицы 3 оказываются равными
s14 = c14 - c'14 = c14 – (α1 + β4) = 80 – 50 = 30,
s22 = c22 - c'22 = c22 – (α2 + β2) = 90 – (10 + 50) = 30,
s23 = c23 - c'23 = c23 – (α2 + β3) = 40 – (10 + 15) = 15,
s31 = c31 - c'31 = c31 – (α3 + β1) = 50 – (– 40 + 70) = 20,
s33 = c33 - c'33 = c33 – (α3 + β2) = 90 – (– 40 + 15) = 115,
s34 = c34 - c'34 = c34 – (α3 + β4) = 11 – (– 40 + 50) = 1.
Алгебраические суммы тарифов для всех свободных клеток таблицы 3 оказались положительными. Следовательно, план перевозок, представленный таблицей 3, является оптимальным.
Ответ: При оптимальном плане перевозок потребность заказчика В1 удовлетворяется как базой А1, из которой поступает 140т. так и базой А2, из которой поступает 30т. ; потребность заказчика В2 удовлетворяется базами А1, из которой поступает 60т. и А3, из которой поступает 50т.; потребность заказчика В3 удовлетворяет база А1 , из которой поступает 100т., а потребность заказчика В4 удовлетворяет база А2, из которой поступает 120т. При этом стоимость перевозок составит
|
|
|
Fопт. = 70 ·140 + 50 · 60 + 15 · 100 + 80 · 30 + 60 ·120 + 10 · 50 = 24400 (т.км.),
что меньше стоимости перевозки по первоначальному плану (Fнач.= 25650 т.км.) на 1250 т.км.
Задания для самостоятельной работы
Расчетная работа 4
Вычислить определитель

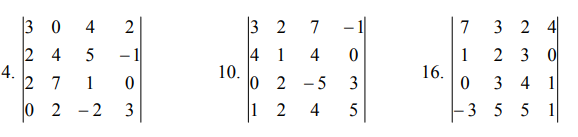
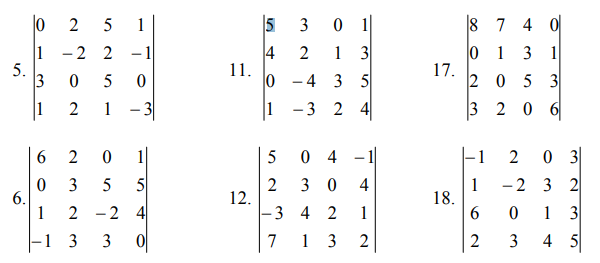

С матрицами А, В, С совершить указанные действия. Найти обратную к матрице А.
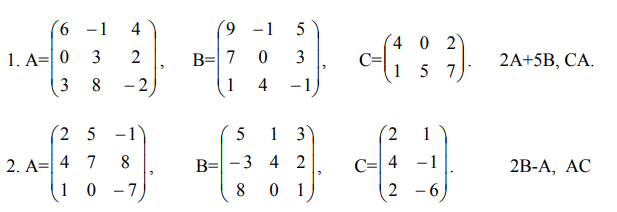
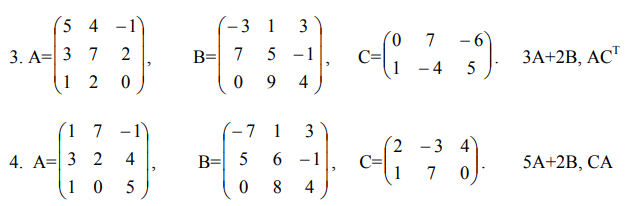

Решить системы линейных уравнений: а) методом Крамера; б) методом Гаусса.
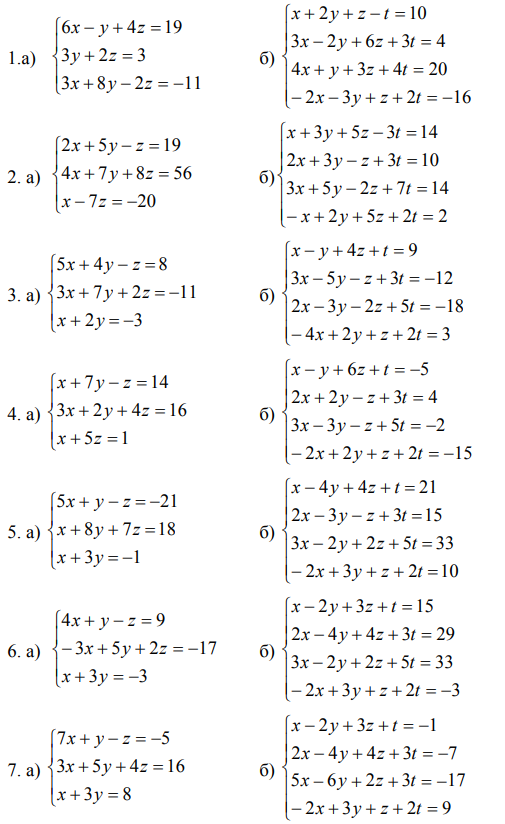
Найти начальное опорное решение методом северо-западного угла и методом минимального элемента.
| 1 | 
| 2 | 
|
| 3 | 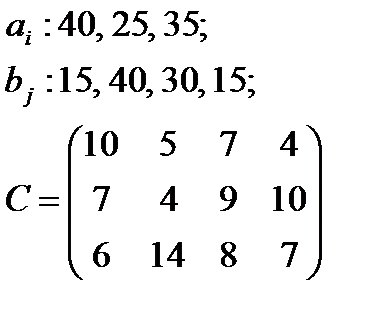
| 4 | 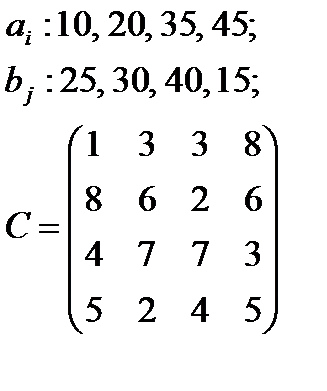
|
| 5 | 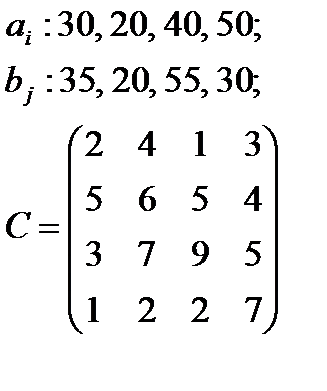
| 6 | 
|
| 7 | 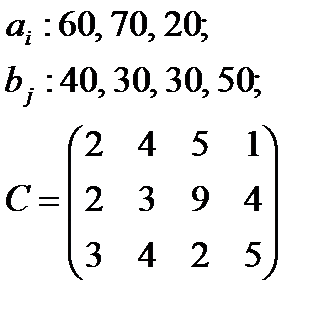
| 8 | 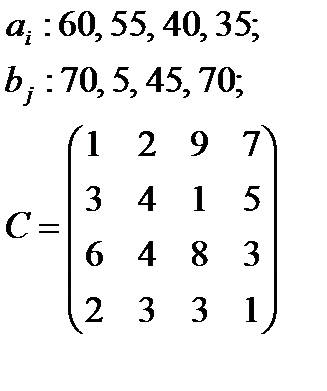
|
5. По указанным ниже данным о ресурсах ai , потребностях bj и матрицы коэффициентов затрат с c оставить математические модели и решить соответствующие транспортные задачи.
|
|
|
| 1 | 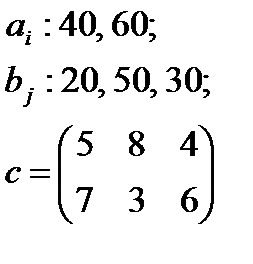
| 2 | 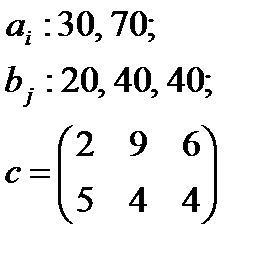
|
| 3 | 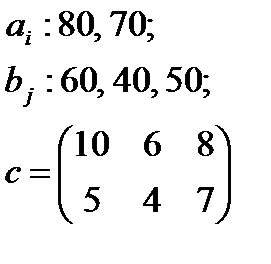
| 4 | 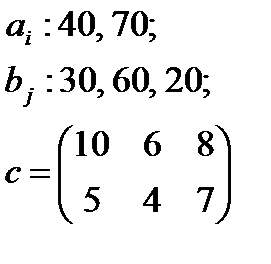
|
| 5 | 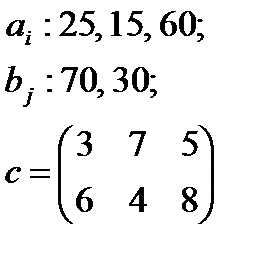
| 6 | 
|
| 7 | 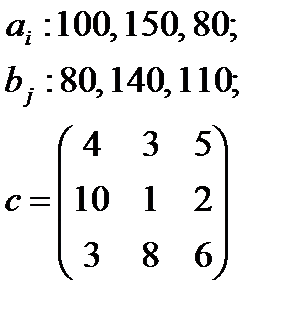
| 8 | 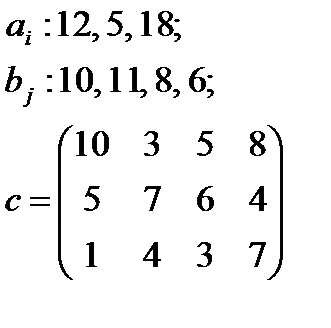
|
| 9 | 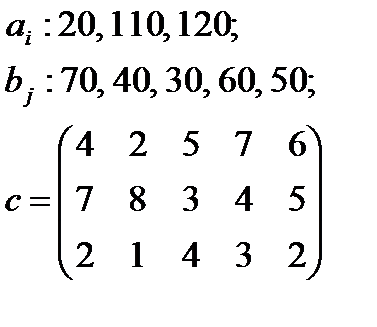
| 10 | 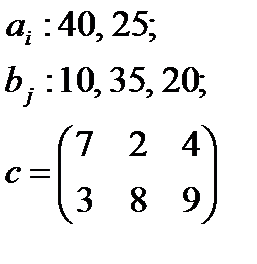
|
| 11 | 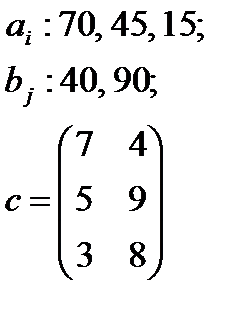
| 12 | 
|
| 13 | 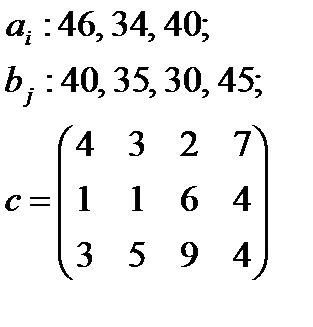
| 14 | 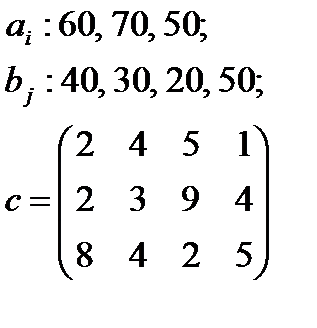
|
РАЗДЕЛ 5.ОСНОВЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
Уравнение прямой
Уравнение окружности
Эллипс
Гипербола
Парабола
Задания для самостоятельной работы
Уравнение прямой
Вначале дадим определение понятия уравнения линии на плоскости.
Пусть на плоскости 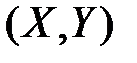 задана некоторая линия
задана некоторая линия 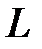 .
.
Уравнение 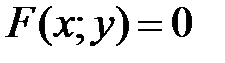 называется уравнением линии
называется уравнением линии 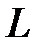 , если выполнены два условия:
, если выполнены два условия:
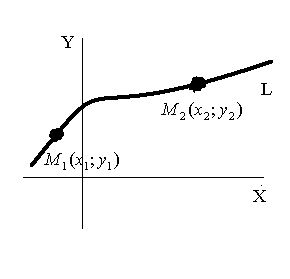
1.для любой точки 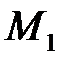 с координатами
с координатами 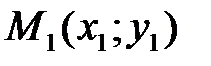 , лежащей на линии
, лежащей на линии 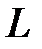 , выполнено
, выполнено  , то есть ее координаты удовлетворяют уравнению линии;
, то есть ее координаты удовлетворяют уравнению линии;
2. любая точка 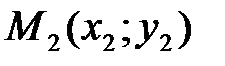 , координаты которой удовлетворяют уравнению
, координаты которой удовлетворяют уравнению 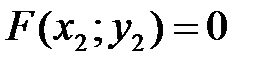 , лежит на линии.
, лежит на линии.
Дата добавления: 2019-09-13; просмотров: 183; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
