Система Кенига. Теорема об изменении кинетического момента относительно центра масс механической системы
|
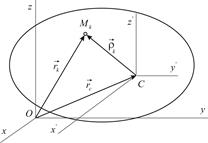
| Рис. 3.2 |
Пусть система отсчета 
неподвижная (инерциальная). Система 
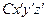движется поступательно по отношению к 
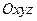, причем ее начало во все время движения совпадает с центром масс механической системы (Рис.3.2). Такая система координат называется системой Кенига. Следует заметить, что система Кенига играет исключительно важную роль при описании движения твердого тела.
Можно показать (доказательство.......), теорема об изменении кинетического момента сохраняет свой вид, если в качестве моментной точки используется центр масс механической системы.
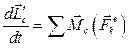(3.13)
Таким образом,
производная по времени от кинетического момента механической системы относительно ее центра масс равна сумме моментов относительно центра масс всех приложенных к системе внешних сил.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
- Как выглядит система дифференциальных уравнений движения точек механической системы?
- Что называется внешними силами?
- Что называется внутренними силами?
- Каковы основные свойства внутренних сил системы?
- Что называется количеством движения механической системы и как оно вычисляется?
- В чём состоит теорема об изменении количества движения механической системы?
- Что называется центром масс механической системы?
- В чём состоит теорема о движении центра масс механической системы?
- Что называется моментом количества движения материальной точки и механической системы?
- В чём состоит теорема об изменении момента количества движения механической системы относительно неподвижного центра?
- Что такое система координат Кёнига?
- В чём состоит теорема об изменении момента количества движения механической системы относительно центра масс механической системы?
|
|
|
ЛЕКЦИЯ 4 (12)
ДИНАМИКА АБСОЛЮТНО ТВЁРДОГО ТЕЛА
Простейшие движения твердого тела
Поступательное движение твердого тела
Как известно из курса кинематики, что поступательное движение твердого тела полностью определяется движением одной любой его точки. Таким образом, все вопросы динамики поступательного движения твердого тела решаются при помощи теоремы о движении центра масс механической системы
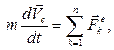(4.1)
которая связывает координаты центра масс тела с приложенными к нему внешними силами. Записывая уравнение (4.1) в проекциях на координатные оси, получаем в общем случае три уравнения движения твердого тела:
|
|
|
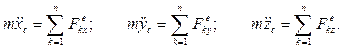
В случае плоского или прямолинейного поступательного движения тела число дифференциальных уравнений движения будет, естественно, меньше.
Если траектория центра масс тела известна, имеет смысл использовать уравнение (4.1) в проекциях на оси естественного трехгранника:
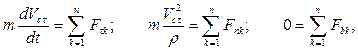
где 
– радиус кривизны траектории центра масс тела.
Вращение твердого тела вокруг неподвижной оси
Пусть абсолютно твердое тело вращается вокруг неподвижной оси под действием системы внешних сил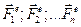 
(как активных, так и реакций связей).
|
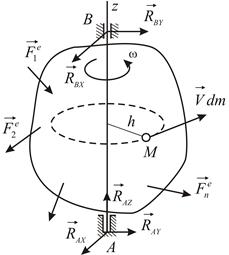
| Рис.4.1 |
Как известно, положение тела, имеющего ось вращения, определяется углом поворота. Для вывода дифференциального уравнения движения используем теорему об изменении кинетического момента относительно неподвижной оси, которую примем за координатную ось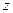 
(Рис.4.1):
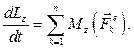(4.2)
Вычислим кинетический момент тела относительно оси вращения. Количество движения 
любой частицы 
тела перпендикулярно оси вращения, причем,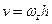 
, где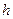 
– кратчайшее расстояние от частицы до оси вращения. Таким образом,
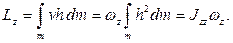
Подставляя полученный результат в уравнение (4.2), получаем дифференциальное уравнение вращательного движения твердого тела:
|
|
|
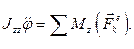(4.3)
Уравнение (4.3) называется дифференциальным уравнением вращательного движения твердого тела. Интегрируя это уравнение, находим угол 
как функцию времени и тем самым полностью определяем движение, поскольку в рассматриваемом случае система имеет одну степень свободы и ее положение вполне определяется углом . Заметим, что неизвестные реакции опор 
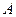и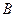 
в уравнение движения (4.3) не входят, так как они не создают момента относительно оси вращения (шарниры считаем идеальными).
Дата добавления: 2019-09-02; просмотров: 1280; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!