ЛИНЕЙНЫЕ КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
Постановка задачи
Пусть материальная точка 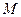 с массой
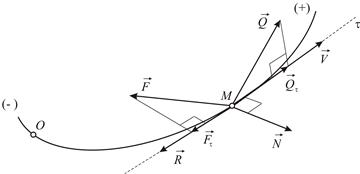
с массой 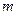 , в силу наложенных на нее связей, движется по известной траектории, на которой установлена криволинейная система отсчета (Рис.2.1). Начало отсчета дуговой координаты
, в силу наложенных на нее связей, движется по известной траектории, на которой установлена криволинейная система отсчета (Рис.2.1). Начало отсчета дуговой координаты 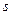 совместим с положением равновесия точки
совместим с положением равновесия точки 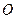 . Пусть среди сил, действующих на точку, есть восстанавливающая сила. Восстанавливающей называется сила, возникающая при смещении точки из положения равновесия и стремящаяся вернуть точку в равновесное положение. Такая сила всегда направлена в сторону положения равновесия, а её модуль пропорционален величине смещения точки из положения равновесия. Проекцию восстанавливающей силы на направление касательной к траектории можно записать в виде
. Пусть среди сил, действующих на точку, есть восстанавливающая сила. Восстанавливающей называется сила, возникающая при смещении точки из положения равновесия и стремящаяся вернуть точку в равновесное положение. Такая сила всегда направлена в сторону положения равновесия, а её модуль пропорционален величине смещения точки из положения равновесия. Проекцию восстанавливающей силы на направление касательной к траектории можно записать в виде 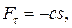 где
где  – коэффициент пропорциональности, который называется коэффициентом жесткости.
– коэффициент пропорциональности, который называется коэффициентом жесткости.
|
| Рис. 2.1 |
Природа таких сил весьма разнообразна (упругие, архимедовы, гравитационные силы и т.п.). В практическом отношении интересны задачи, в которых кроме восстанавливающей силы на точку действует сила сопротивления 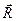 и некоторая сила
и некоторая сила 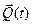 , которую называют возмущающей силой.
, которую называют возмущающей силой.
Поскольку траектория точки считается известной, для определения закона движения используем уравнение:
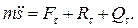 (2.2)
(2.2)
Ограничиваясь случаем пропорциональности силы сопротивления первой степени скорости (вязкое трение при малых скоростях), получаем: 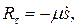 где
где 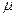 – коэффициент пропорциональности.
– коэффициент пропорциональности.
|
|
|
Рассмотрим случай периодической возмущающей силы:
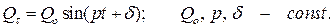 (2.4)
(2.4)
Таким образом, дифференциальное уравнение движения (2.2) принимает вид:
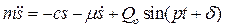 или
или 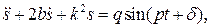 (2.5)
(2.5)
где обозначено:
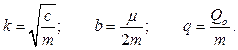 (2.6)
(2.6)
Задача состоит в определении решения уравнения (2.5) при заданных начальных условиях:
при 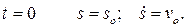 (2.7)
(2.7)
Следует отметить, что многие функции 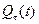 при определенных условиях могут быть представлены на интервале движения разложением в ряд Фурье, т.е. в виде суммы (вообще говоря, бесконечной), каждый член которой имеет вид (2.4). Тогда решение уравнения движения, в силу его линейности, может быть представлено соответствующей суммой решений уравнений вида (2.5). Таким образом, рассматриваемый случай возмущающей силы является довольно общим.
при определенных условиях могут быть представлены на интервале движения разложением в ряд Фурье, т.е. в виде суммы (вообще говоря, бесконечной), каждый член которой имеет вид (2.4). Тогда решение уравнения движения, в силу его линейности, может быть представлено соответствующей суммой решений уравнений вида (2.5). Таким образом, рассматриваемый случай возмущающей силы является довольно общим.
|
|
|
Движение точки под действием восстанавливающей силы
Пусть на точку действует только восстанавливающая сила. Полагая в уравнении (2.5) 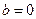 и
и 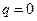 , получаем:
, получаем:
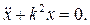 (2.8)
(2.8)
Здесь и в дальнейшем полагаем 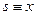 , имея ввиду, что в учебной литературе обычно рассматривается случай прямолинейного движения, хотя все полученные результаты справедливы для движения точки по любой криволинейной траектории.
, имея ввиду, что в учебной литературе обычно рассматривается случай прямолинейного движения, хотя все полученные результаты справедливы для движения точки по любой криволинейной траектории.
Уравнение (2.8) представляет собой обыкновенное линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами.
Общее решение уравнения (2.8) имеет вид:
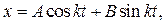 (2.9)
(2.9)
где 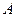 и
и 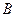 — постоянные интегрирования.
— постоянные интегрирования.
Дифференцируя решение (2.9) по времени, получаем закон изменения скорости точки:
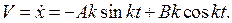 (2.10)
(2.10)
Для определения постоянных интегрирования 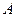 и
и 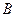 подставляем начальные условия, которые в принятых нами обозначениях имеют вид
подставляем начальные условия, которые в принятых нами обозначениях имеют вид
|
|
|
при 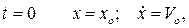 (2.11)
(2.11)
в уравнения (10.9) и (10.10). Получаем: 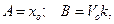 так что общее решение уравнения (10.8) принимает вид:
так что общее решение уравнения (10.8) принимает вид:
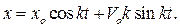 (2.12)
(2.12)
или
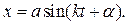 (2.13)
(2.13)
|
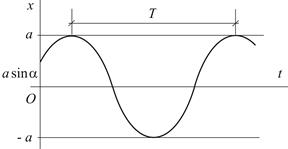
| Рис. 2.2 |
Скорость точки при этом вычисляется по формуле:
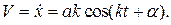 (2.14)
(2.14)
Движение, совершаемое точкой под действием восстанавливающей силы, называется простым гармоническим или свободным незатухающим колебанием (Рис.2.2).
Постоянная 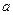 определяет наибольшее отклонение точки от положения равновесия; ее называют амплитудой колебаний. Величина
определяет наибольшее отклонение точки от положения равновесия; ее называют амплитудой колебаний. Величина 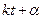 , определяющая положение и скорость точки в данный момент времени, называется фазой колебаний;
, определяющая положение и скорость точки в данный момент времени, называется фазой колебаний; 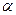 – начальная фаза.
– начальная фаза.
Как видно, движение будет периодическим. Периодом колебаний называется промежуток времени 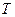 , в течение которого точка совершает одно полное колебание
, в течение которого точка совершает одно полное колебание
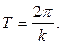 (2.15)
(2.15)
|
|
|
Величина 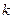 , пропорциональная
, пропорциональная 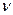 , называется круговой или циклической частотой колебаний.
, называется круговой или циклической частотой колебаний.
Дата добавления: 2019-09-02; просмотров: 251; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
