Координатный способ задания движения точки.
 При этом способе задается 3 функции (при движении в пространстве), определяющие три координаты точки в каждый момент времени. Системы координат могут быть разными, например: прямоугольная декартова, цилиндрическая или сферическая система координат. В первом случае задается: х=х( t ); y =у( t ); z = z ( t ) - это и есть уравнения движения точки (рис.2). в цилиндрической системе координат (рис.3) задаются: ρ= ρ( t ); φ= φ ( t ); z = z ( t ). В сферической (рис.4): φ = φ( t ); θ= θ( t ); r = r ( t ) . если движение задано в какой - то из этих систем координат, то всегда можно перейти к заданию движения в любой из двух других.
При этом способе задается 3 функции (при движении в пространстве), определяющие три координаты точки в каждый момент времени. Системы координат могут быть разными, например: прямоугольная декартова, цилиндрическая или сферическая система координат. В первом случае задается: х=х( t ); y =у( t ); z = z ( t ) - это и есть уравнения движения точки (рис.2). в цилиндрической системе координат (рис.3) задаются: ρ= ρ( t ); φ= φ ( t ); z = z ( t ). В сферической (рис.4): φ = φ( t ); θ= θ( t ); r = r ( t ) . если движение задано в какой - то из этих систем координат, то всегда можно перейти к заданию движения в любой из двух других.
Естественный способ задания движения точки.
 Он заключается в задании (рис.5):
Он заключается в задании (рис.5):
1) траектории точки: у = f (х),
2) начала отсчета (точка О),
3) положительного направления отсчета,
4) закона движения s = s(t), где s - дуговая
координата.
Естественные оси координат.
Естественные оси двигаются вместе с точкой и изменяют свое положение в пространстве. Этих осей три (рис.6):
касательная, главная нормаль, 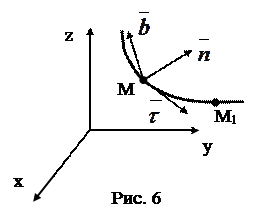 бинормаль.
бинормаль.
Единичный вектор касательной - 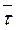 (тау) направлен по касательной к траектории в сторону положительного отсчета дуги.
(тау) направлен по касательной к траектории в сторону положительного отсчета дуги.
Соприкасающаяся плоскость - предельное положение плоскости, проходящей через т. М1, лежащую на кривой и касательную в
т. М, при стремлении т. М1 к т. М. Единичный вектор главной нормали 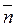 - перпендикулярен
- перпендикулярен 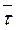 , лежит в соприкасающейся плоскости и направлен в сторону вогнутости траектории. Плоскость перпендикулярная касательной называется нормальной. Единичный вектор бинормали
, лежит в соприкасающейся плоскости и направлен в сторону вогнутости траектории. Плоскость перпендикулярная касательной называется нормальной. Единичный вектор бинормали  - перпендикулярен соприкасающейся плоскости и направлен в ту сторону, откуда вращение от
- перпендикулярен соприкасающейся плоскости и направлен в ту сторону, откуда вращение от 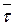 к
к 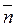 , по кратчайшему пути, видно происходящим против часовой стрелки. Плоскость (
, по кратчайшему пути, видно происходящим против часовой стрелки. Плоскость ( 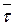 ,
, 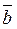 ) называется спрямляющей.
) называется спрямляющей.
|
|
|
Скорость при векторном способе задания движения.
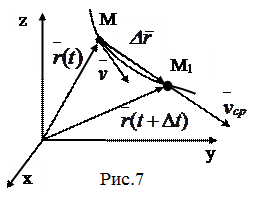
Пусть за время Δt точка переместилась из М в М 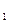 (рис.7) , вектор Δ
(рис.7) , вектор Δ 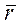 - вектор перемещения. Средней скоростью точки за время Δt называется вектор
- вектор перемещения. Средней скоростью точки за время Δt называется вектор 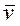 ср = Δ
ср = Δ 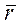 /Δt. Скоростью точки в данный момент времени называется предел, к которому стремится отношение вектора перемещения к промежутку времени, за которое оно произошло, при стремлении последнего к нулю :
/Δt. Скоростью точки в данный момент времени называется предел, к которому стремится отношение вектора перемещения к промежутку времени, за которое оно произошло, при стремлении последнего к нулю :
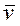 = lim Δ
= lim Δ 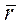 /Δt
/Δt
Δt 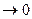
Из рис. 7 видно, что: 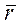 ( t ) + Δ
( t ) + Δ 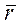 =
= 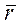 ( t +Δ t ) тогда: Δ
( t +Δ t ) тогда: Δ 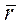 =
= 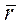 ( t +Δ t ) -
( t +Δ t ) - 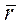 ( t ), и
( t ), и
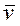 = lim Δ
= lim Δ 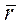 /Δt = lim(
/Δt = lim( 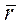 (t+Δt) -
(t+Δt) - 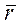 (t)) / Δt = d
(t)) / Δt = d 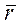 / dt.
/ dt.
Δt 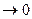 Δt
Δt 
то есть, скорость точки в данный момент времени равна первой производной от радиуса вектора по времени. Из рисунка видно, что вектор скорости в данный момент времени занимает положение касательной. Скорость измеряется в м/с.
6 . Ускорение при векторном способе задания движения.
|
|
|
Средним ускорением называется отношение вектора изменения скорости к промежутку времени, за которое оно произошло: 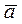 ср=Δ
ср=Δ 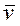 /Δt.
/Δt.
 Ускорением точки в данный момент называется предел этого отношения при стремлении промежутка времени к нулю.
Ускорением точки в данный момент называется предел этого отношения при стремлении промежутка времени к нулю.
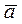 = lim Δ
= lim Δ 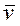 / Δ t = lim(
/ Δ t = lim( 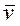 (t+ Δ t) -
(t+ Δ t) - 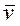 (t))/ Δ t.
(t))/ Δ t.
Δ t 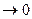 Δ t
Δ t 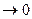
Ускорение равно первой производной от скорости или второй производной от радиуса вектора по времени:
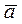 = d
= d 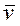 / dt = d
/ dt = d 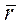 / dt
/ dt 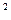 .
.
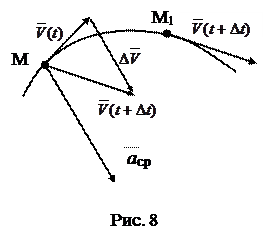
Ускорение 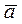 ср, а значит и ускорение в данный момент времени -
ср, а значит и ускорение в данный момент времени -  направлено в сторону вогнутости траектории (рис.8). Ускорение измеряется в м/с2.
направлено в сторону вогнутости траектории (рис.8). Ускорение измеряется в м/с2.
7 . Скорость при координатном способе задания движения.
Известно, что: 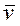 = d
= d 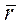 / dt,но
/ dt,но 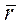 = x ·
= x · 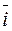 + y ·
+ y · 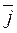 + z ·
+ z · 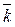 , тогда (т.к.
, тогда (т.к. 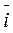 ,
, 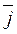 ,
,  - const):
- const):
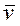 = dx / dt ·
= dx / dt · 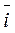 + dy / dt ·
+ dy / dt · 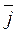 + dz / dt ·
+ dz / dt · 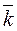 , (1)
, (1)
С другой стороны: 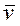 = v
= v 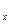 ·
· 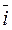 + v
+ v 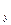 ·
· 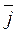 + v
+ v  ·
·  . (2)
. (2)
сравнивая (1) и (2) получим: v х = dx / dt ; v у = dy / dt ; v  = dz / dt, т.е. проекция скорости на ось равна первой производной от соответствующей координаты по времени. Зная проекции можно найти модуль скорости:
= dz / dt, т.е. проекция скорости на ось равна первой производной от соответствующей координаты по времени. Зная проекции можно найти модуль скорости:
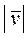 =
= 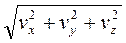 , а так же направляющие косинусы:
, а так же направляющие косинусы:
соs( 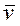 ;
; 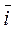 ) = vx / |
) = vx / | 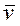 | ; соs(
| ; соs( 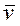 ;
; 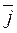 ) = vy / |
) = vy / | 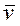 |; соs(
|; соs( 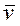 ;
; 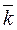 ) = vz / |
) = vz / | 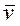 |.
|.
8. Ускорение при координатном способе задания движения.
|
|
|
Известно, что: 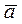 = d
= d 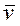 / dt, но
/ dt, но 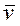 = vx ·
= vx · 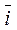 + v y ·
+ v y · 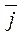 + vz ·
+ vz · 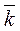 , тогда:
, тогда:
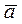 = dv x /d t ·
= dv x /d t · 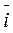 +dvy /d t ·
+dvy /d t · 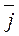 +dvz /dz ·
+dvz /dz ·  , (1)
, (1)
с другой стороны : 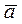 = ах ·
= ах ·  + ау ·
+ ау · 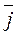 + а z ·
+ а z · 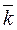 . (2)
. (2)
сравнивая (1) и (2) получим:
а x = dv x / dt = d 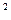 x / dt
x / dt 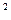 ; а y = dvy / dt = d
; а y = dvy / dt = d 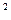 y / dt
y / dt 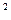 ; а
; а  = dvz / dt = d
= dvz / dt = d 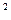 z / dt
z / dt 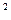 . то есть: проекция ускорения на ось равна первой производной от проекции скорости на ту же ось, или второй производной от соответствующей координаты по времени.
. то есть: проекция ускорения на ось равна первой производной от проекции скорости на ту же ось, или второй производной от соответствующей координаты по времени.
Модуль ускорения : | 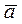 | =
| = 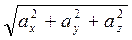 , направляющие косинусы:
, направляющие косинусы:
соs ( 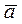 ;
; 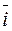 ) = а x / |
) = а x / | 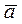 | ; соs(
| ; соs( 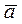 ;
; 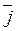 ) = а y / |
) = а y / | 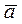 |; соs (
|; соs (  ;
; 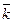 ) = а z / |
) = а z / |  |.
|.
Дата добавления: 2019-09-02; просмотров: 301; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
