С эллипсом связаны две прямые, называемые директрисами. Их уравнения :
x = a/e; x = -a/e.
Теорема. Для того, чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.
Пример. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса, заданного уравнением :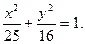 
1) Координаты нижней вершины: x = 0; y 2 = 16; y = -4.
2) Координаты левого фокуса: c 2 = a 2 – b 2 = 25 – 16 = 9; c = 3; F 2 (-3; 0).
3) Уравнение прямой, проходящей через две точки:
Пример. Составить уравнение эллипса, если его фокусы F 1 (0; 0), F 2 (1; 1), большая ось равна 2.
Уравнение эллипса имеет вид: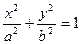 
. Расстояние между фокусами:
2 c = 
, таким образом, a 2 – b 2 = c 2 = ½
по условию 2а = 2, следовательно, а = 1, b = 
Итого: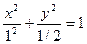 
.
Гипербола.
Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.
y
B M(x, y)
r1
r2
F1 a F2
C
По определению ï r 1 – r 2 ï = 2 a . F 1 , F 2 – фокусы гиперболы. F 1 F 2 = 2 c .
|
|
|
Выберем на гиперболе произвольную точку М(х, у). Тогда :
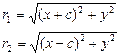
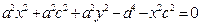
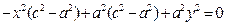
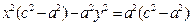
обозначим с2 – а2 = b 2 (геометрически эта величина – меньшая полуось)
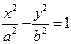
Получили каноническое уравнение гиперболы.
Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.
Ось 2а называется действительной осью гиперболы.
Ось 2 b называется мнимой осью гиперболы.
Гипербола имеет две асимптоты, уравнения которых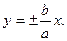 
Определение. Отношение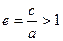 
называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.
С учетом того, что с2 – а2 = b 2 :
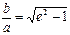
Если а = b , e = 
, то гипербола называется равнобочной (равносторонней).
Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: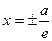 
.
Теорема. Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r / d – величина постоянная, равная эксцентриситету.
|
|
|
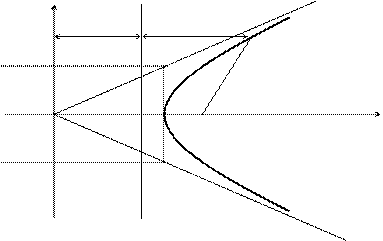
Доказательство. Изобразим схематично гиперболу.
y
A / e d
M ( x , y )
r 1
0 a F 1 x
OF 1 = c
Из очевидных геометрических соотношений можно записать:
a / e + d = x , следовательно d = x – a / e .
( x – c )2 + y 2 = r 2
Из канонического уравнения: 
, с учетом b 2 = c 2 – a 2 :
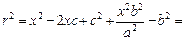
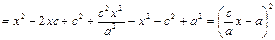
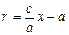
Тогда т . к . с /a = e, то r = ex – a.
Итого: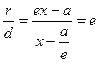 
.
Для левой ветви гиперболы доказательство аналогично. Теорема доказана.
Пример. Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих вершинах и фокусах эллипса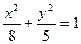 
.
Для эллипса: c 2 = a 2 – b 2 .
Для гиперболы: c 2 = a 2 + b 2 . 
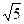
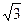
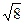
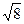
Уравнение гиперболы: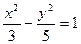 
.
Пример. Составить уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением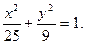 
|
|
|
Находим фокусное расстояние c 2 = 25 – 9 = 16.
Для гиперболы: c 2 = a 2 + b 2 = 16, e = c / a = 2; c = 2 a ; c 2 = 4 a 2 ; a 2 = 4;
b 2 = 16 – 4 = 12.
Итого: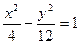 
- искомое уравнение гиперболы.
Парабола.
Определение. Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.
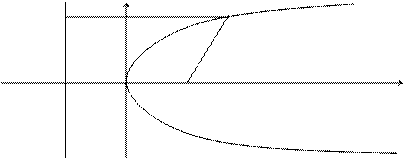Расположим начало координат посередине между фокусом и директрисой.
У
А М(х, у)
 | |||
 | |||
О F x
 |
P /2 p /2
Дата добавления: 2019-02-12; просмотров: 222; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!