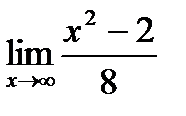Первый и второй замечательные пределы.
 Рис. 1 Рис. 1
| Первый замечательный предел.
Вывод первого замечательного предела представляет интерес с точки зрения приложения теории пределов, и поэтому мы предлагаем Вам его практически целиком.
Рассмотрим поведение функции 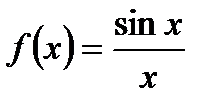 при при 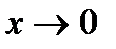 . Для этого рассмотрим окружность радиуса 1; обозначим центральный угол МОВ через х, при этом . Для этого рассмотрим окружность радиуса 1; обозначим центральный угол МОВ через х, при этом 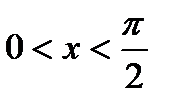 . .
|
Тогда явно площадь DМОА < площадь сектора МОА < площадь DСОА (см. рис. 1).
S DМОА = 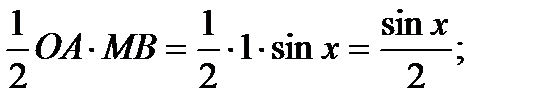
S МОА= 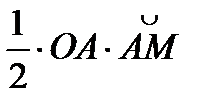 =
= 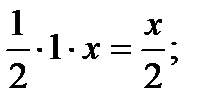 S DCОА=
S DCОА= 
Вернувшись к упомянутому неравенству и удвоив его, получим:
sin x < x < tg x.
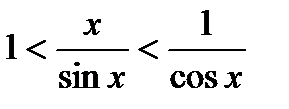 или
или 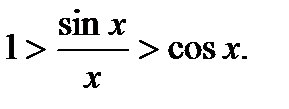
Поскольку 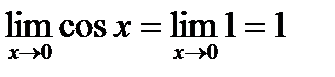 , то переменная
, то переменная 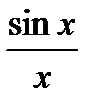 заключена между двумя величинами, имеющими один и тот же предел, т.е. , на основании теоремы о пределе промежуточной функции предыдущего пункта имеем:
заключена между двумя величинами, имеющими один и тот же предел, т.е. , на основании теоремы о пределе промежуточной функции предыдущего пункта имеем:
- первый замечательный предел.
Пример. Вычислите пределы функций, используя первый замечательный предел:
1) 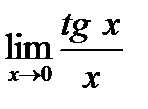 ; 2)
; 2) 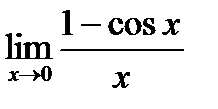 ; 3)
; 3) 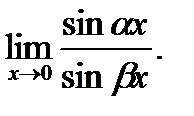
Решение.
1) Разложим 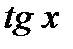 как отношение
как отношение  и объединим множители по вышеуказанной схеме:
и объединим множители по вышеуказанной схеме:
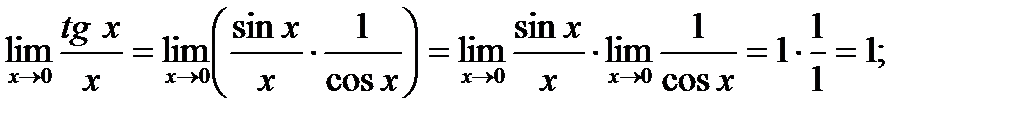
2) Применяя формулу 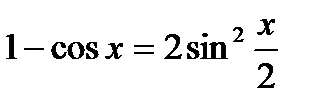 , произведем подстановку и получим:
, произведем подстановку и получим:
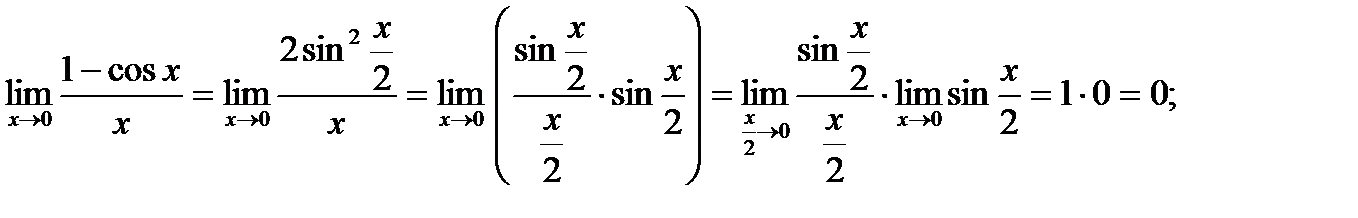
3) Разделим числитель и знаменатель дроби на х, затем выровняем сложные аргументы, компенсируя преобразование добавочным коэффициентом 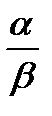 и получим:
и получим:
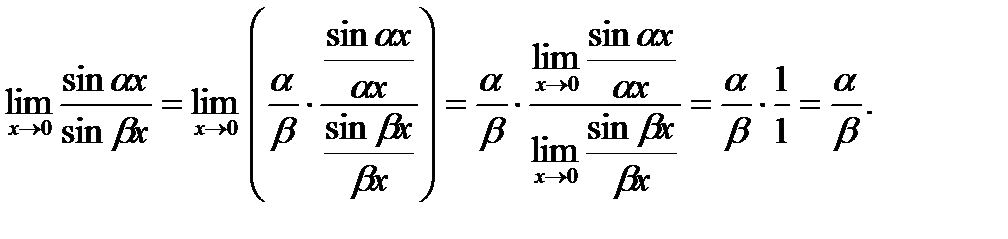
Ответ. 1) 1, 2) 0, 3) 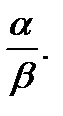
Задание: Вычислите предел функции, используя первый замечательный предел:
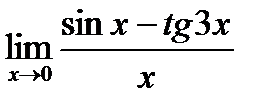
Решение:
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________Ответ:-2.
Второй замечательный предел.
Для вывода второго замечательного предела введем определение числа е:
Определение. Предел переменной величины 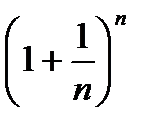 при
при  называется числом е:
называется числом е:
- второй замечательный предел
Число е – иррациональное число. Его значение с десятью верными знаками после запятой обычно округляют до одного верного знака после запятой:
e = 2,7182818284…» 2,7.
Теорема. Функция 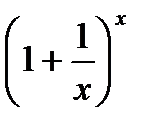 при х, стремящемся к бесконечности, стремится к пределу е:
при х, стремящемся к бесконечности, стремится к пределу е:
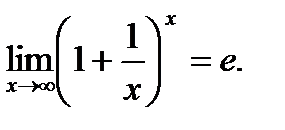
Пример. Вычислите пределы функций:
1) 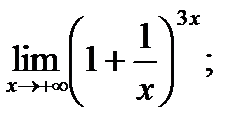 2)
2) 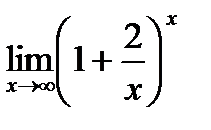 ; 3)
; 3) 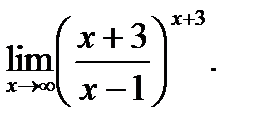
Решение.
1)

2) Введем новую переменную с целью свести предел ко второму замечательному пределу:  , отсюда
, отсюда 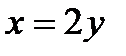 . При
. При 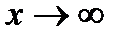 имеем
имеем 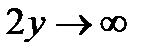 , т. е.
, т. е. 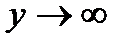 .
.
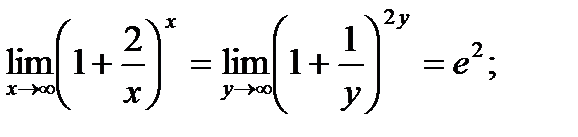
Кроме того, аналогичным образом можно доказать, что 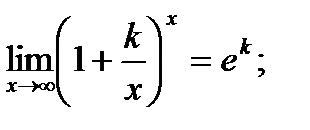
3) Разложив числитель данной дроби на слагаемые, добьемся выделения 1, а затем примем 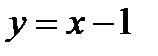 и используем упомянутое выше утверждение:
и используем упомянутое выше утверждение:
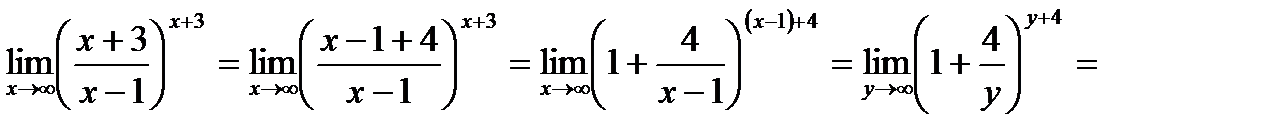
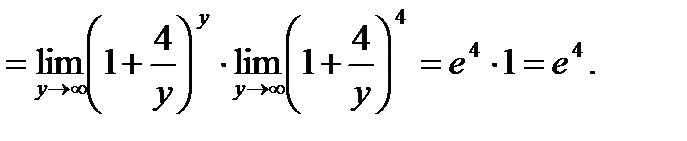
Ответ. 1) е3 , 2) е2, 3) е4.
Задание. Вычислите предел функции, используя второй замечательный предел:
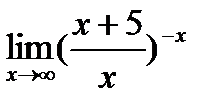
Решение:
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
 Ответ: е-5
Ответ: е-5
Непрерывность функции
Непрерывность функции в точке
Определение. Функция f( x), x Î ( a; b) называется непрерывной в точке xо Î ( a; b), если предел функции f( x) в точке хо существует и равен значению функции в этой точке:
 .
.
Согласно данному определению, непрерывность функции f( x) в точке хо означает выполнимость следующих условий:
1) функция f( x) должна быть определена в точке хо;
2) у функции f( x) должен существовать предел в точке хо;
3) предел функции f( x) в точке хо должен совпадать со значением функции в этой точке.
Пример.
Функция f( x) = x2 определена на всей числовой прямой и непрерывна в точке х = 1 поскольку f(1) = 1 и 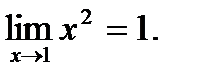
Непрерывность функции на множестве
Определение. Функция f(x), называется непрерывной на интервале (a; b), если она непрерывна в каждой точке этого интервала.
Если функция непрерывна в некоторой точке, то эта точка называется точкой непрерывности данной функции. В тех случаях, когда предел функции в данной точке не существует или его значение не совпадает со значением функции в данной точке, то функция называется разрывной в этой точке, а сама точка – точкой разрыва функции f(x).
Свойства непрерывных функций.
1) Сумма конечного числа функций, непрерывных в точке а, есть функция, непрерывная в этой точке.
2) Произведение конечного числа функций, непрерывных в точке а, есть функция, непрерывная в этой точке.
3) Отношение конечного числа функций, непрерывных в точке а, есть функция, непрерывная в этой точке, если значение функции, стоящей в знаменателе, отлично от нуля в точке а.
Пример.
1) Функция f( x) = xп, где n Î N, непрерывна на всей числовой прямой. Доказать этот факт можно, используя свойство 2 и непрерывность функции f( x) = x.
2) Функция f( x) = с xп (с – константа) непрерывна на всей числовой прямой, исходя из свойства 2 и примера 1.
Теорема 2. Любая дробно-рациональная функция непрерывна в каждой точке своей области определения.
Пример.
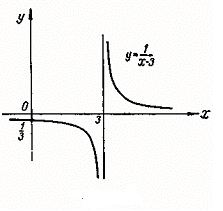
1) Функция 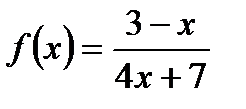 непрерывна на всей числовой прямой, кроме точки
непрерывна на всей числовой прямой, кроме точки 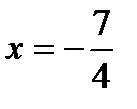 , в которой знаменатель дроби обращается в нуль.
, в которой знаменатель дроби обращается в нуль.
2)
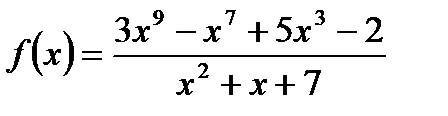 непрерывна всюду на R, т.к. знаменатель нигде не обращается в нуль.
непрерывна всюду на R, т.к. знаменатель нигде не обращается в нуль.
Определение Функция f( x) называется непрерывной в точке х = а, если в этой точке ее приращение  стремится к нулю, когда приращение аргумента
стремится к нулю, когда приращение аргумента 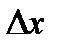 стремится к нулю, или иначе: функция f (х) называется непрерывной в точке х = а , если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т. е. если
стремится к нулю, или иначе: функция f (х) называется непрерывной в точке х = а , если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т. е. если 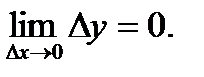
Односторонние пределы функции*
Левосторонний предел функции.Если отыскивается предел функции f( x) при условии, что х, стремясь к а, может принимать только такие значения, которые меньше а, то этот предел, если он существует, называется левосторонним пределом функции f (х) (или левым пределом функции).
Для того чтобы показать, что х стремится к а, оставаясь меньше а, употребляется запись: 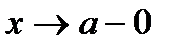 , а левосторонний предел функции обозначается символом:
, а левосторонний предел функции обозначается символом: 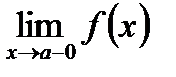 .
.
Правосторонний предел функции.Если отыскивается предел функции f( x) при условии, что х, стремясь к а, может принимать только такие значения, которые больше а, то этот предел, если он существует, называется правосторонним пределом функции f( x) (или правым пределом функции).
То, что х, стремясь к а, остается больше а, обозначается так: 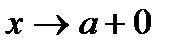 , а правосторонний предел функции обозначается символом:
, а правосторонний предел функции обозначается символом:  .
.
Очевидно, что предел функции при 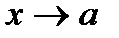 существует только тогда, когда существуют и равны между собой ее левосторонний и правосторонний пределы, т. е. когда
существует только тогда, когда существуют и равны между собой ее левосторонний и правосторонний пределы, т. е. когда 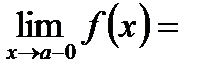
 .
.
Определение Функция f( x) называется непрерывной при х = а, если ее левосторонний и правосторонний пределы существуют, между собой равны и равны значению функции в этой точке, т. е. f( a). То есть:
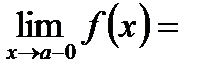
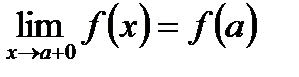 .
.
Точки разрыва и их классификация*
Если равенство 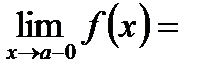
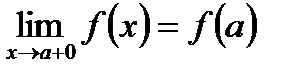 в какой-либо его части не выполняется, то о точке
в какой-либо его части не выполняется, то о точке 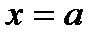 говорят, что она является точкой разрыва.
говорят, что она является точкой разрыва.
Точка разрыва первого рода
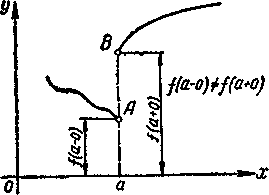 Рис. 2 Рис. 2
|
Определение. Если левосторонний предел функции и ее правосторонний предел существуют, но не равны, между собой, т. е. если
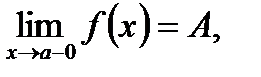 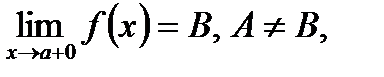 то точка а называется точкой разрыва первого рода (см. рис. 2).
то точка а называется точкой разрыва первого рода (см. рис. 2).
|
Точка разрыва второго рода
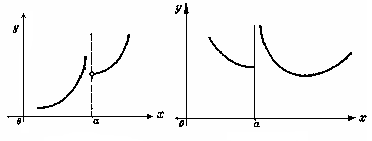 а) б) а) б)
| Определение. Если в точке х = а не существует конечный левосторонний или правосторонний предел функции или оба одновременно, то эта точка называется точкой разрыва второго рода. На рис. 3, а отсутствует левосторонний предел функции; на рис. 3, б – нет правостороннего предела функции. |
| Рис. 3 |
Рис. 4
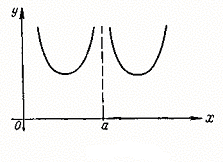
| На рис. 4 представлен график функции, которая не имеет в точке х = а ни левостороннего, ни правостороннего предела. Во всех этих случаях говорят, что функция в точке х = а терпит разрыв второго рода (иначе: точка х = а — точка разрыва второго рода). |
Устранимый разрыв
Определение. Если в точке х = а функция f( x) имеет левосторонний и правосторонний пределы и эти пределы между собой равны, но их значения не совпадают со значением функции в точке а, т. е. со значением f( a), то точка х = а называется точкой устранимого» разрыва.
Таким образом, в этом случае 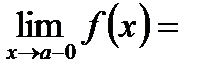
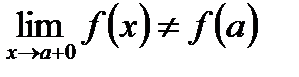 . Разрыв «устраняется» тем, что полагают
. Разрыв «устраняется» тем, что полагают 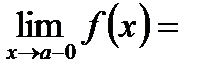
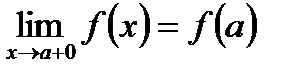 , т. е. принимают, что
, т. е. принимают, что 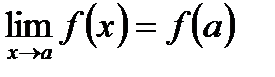 .
.
Пример. Пользуясь определением непрерывности функции через предел 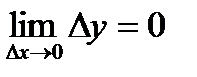 , докажем, что функция
, докажем, что функция 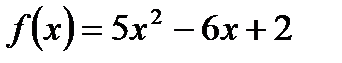 непрерывна в произвольной точке.
непрерывна в произвольной точке.
Решение. Выразим приращение функции при произвольном приращении аргумента в некоторой точке х:
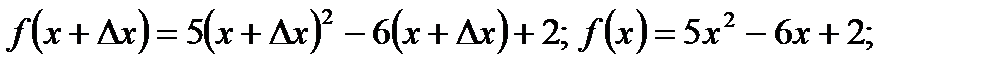
Подставим полученные выражения в формулу приращения функции, и после упрощения получим:
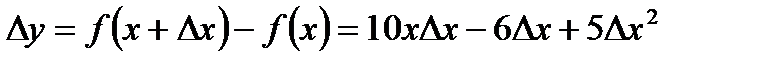 .
.
Найдем предел приращения функции при приращении аргумента, стремящемся к 0:
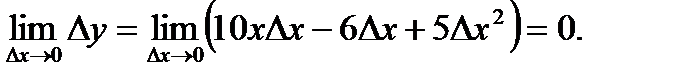
В итоге получаем, что при любом значении х предел приращения функции равен нулю, что доказывает ее непрерывность при любом значении х.
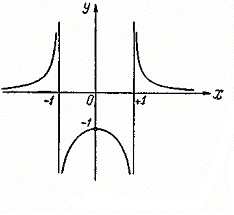
Пример. Исследуем на непрерывность при х = 1 следующую функцию:
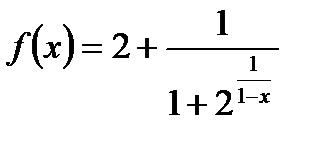 .
.
Решение. Так как знаменатель 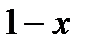 дроби равен нулю при
дроби равен нулю при 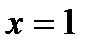 , то функция разрывна при
, то функция разрывна при 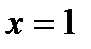 . Установим характер этой точки разрыва. Найдем сначала левосторонний предел функции:
. Установим характер этой точки разрыва. Найдем сначала левосторонний предел функции:
Если 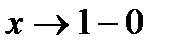 , то можно представить
, то можно представить 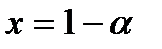 ,
, 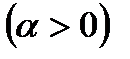 и считать, что
и считать, что 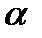 , оставаясь положительной, стремится к нулю. Заменяя х на
, оставаясь положительной, стремится к нулю. Заменяя х на 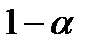 , получим:
, получим:
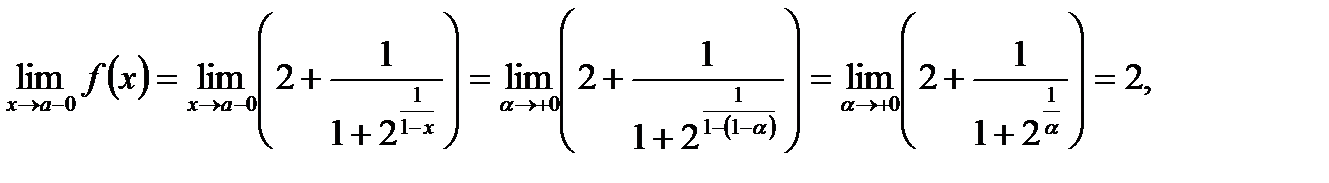
так как при  величина
величина 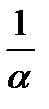 бесконечно большая,
бесконечно большая, 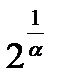 также бесконечно велика,
также бесконечно велика, 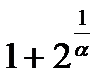 – бесконечно большая величина, обратная ей величина
– бесконечно большая величина, обратная ей величина 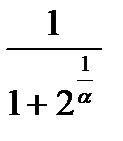 бесконечно мала:
бесконечно мала: 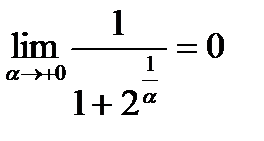 , а потому
, а потому 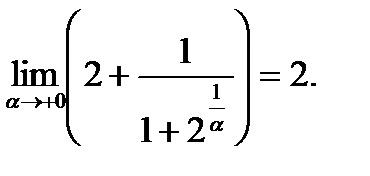
Теперь определим правосторонний предел функции. Если х →1 + 0, можно положить х = 1 + α (α > 0) и считать, что α, оставаясь положительной, стремится к нулю.
Тогда, заменяя х на 1 + α, получим:
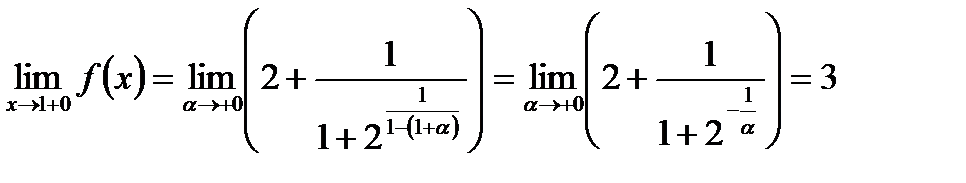 ,
,
| .) |
 величина
величина 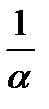 бесконечно большая,
бесконечно большая, 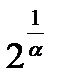 также бесконечно велика,
также бесконечно велика, 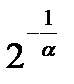 – величина бесконечно малая, т.е. ее предел будет равен 0.
– величина бесконечно малая, т.е. ее предел будет равен 0.
Итак, у функции существуют и левосторонний предел, равный 2, и правосторонний предел, равный 3, но между собой они не равны. Из этого мы заключаем, что точка 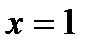 является для заданной функции точкой разрыва первого рода.
является для заданной функции точкой разрыва первого рода.
Пример. Построим графики и определим, какого рода разрыв имеет функция в данной точке (если точка не указана, определим точки разрыва самостоятельно):
1) 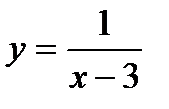 ,
,  2)
2) 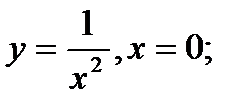 3)
3) 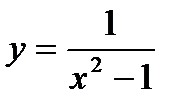 .
.
Решение.
1) в точке  функция имеет разрыв второго рода, поскольку не имеет в этой точке ни одного конечного предела (см. рис. 5, а).
функция имеет разрыв второго рода, поскольку не имеет в этой точке ни одного конечного предела (см. рис. 5, а).
2) в точке 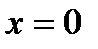 функция имеет разрыв второго рода, поскольку не имеет в этой точке ни одного конечного предела (см. рис. 5, в).
функция имеет разрыв второго рода, поскольку не имеет в этой точке ни одного конечного предела (см. рис. 5, в).
3) функция имеет точки разрыва 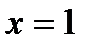 и
и 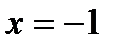 . В обеих точках функция имеет разрыв второго рода (см. рис. 5, б).
. В обеих точках функция имеет разрыв второго рода (см. рис. 5, б).
|
| 
| |
| а) | б) | в) |
| Рис. 5 | ||
Вопросы для самоконтроля
- Дайте определение предела последовательности.
- Дайте определение предела функции.
- Сформулируйте теоремы о пределе функции.
- Дайте определения бесконечно малых и бесконечно больших функций.
- Назовите основные неопределенности при вычислении пределов функции.
- Объясните основные методы раскрытия неопределенностей.
- Дайте определение непрерывной функции.
- Дайте определение точек разрыва функции 1 и 2 рода*.
Контрольные задания
Вычислить пределы функции:
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________________________________________________________
Дата добавления: 2019-01-14; просмотров: 578; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!