Рекомендации по конспектированию
Конспект — сложная запись содержания исходного текста, включающая в себя заимствования (цитаты, формулы, определения) наиболее примечательных мест в соответствии с планом источника, а также сжатый анализ записанного материала и выводы по нему.
Общий порядок работы над конспектом:
¾ определение структуры конспектируемого материала, при этом очень помогает составление плана по ходу изучения текста;
¾ отбор и последующая запись наиболее существенного содержания текста в форме цитат, доказательств или близкого изложения без потерь смысла;
¾ анализ записей и на его основе дополнение наиболее сложных элементов текста;
¾ комментарии (располагать их можно на полях или в виде сносок);
¾ завершение формулирования и запись выводов по каждой из частей текста, а также общих выводов в заключении.
Рекомендации по решению задач
Хорошее усвоение теоретического материала невозможно без решения задач. Многочисленные формулы запомнить трудно, в процессе же решения задач они запоминаются легче. Поэтому в каждой теме содержатся задачи и упражнения, рекомендованные для самостоятельного решения. Темы и задания, отмеченные * - повышенной трудности, выполняются по желанию студента.
Приступая к решению задачи, необходимо внимательно прочесть условие и, уяснив смысл, записать кратко, используя математические символы, условие и искомые результаты. Затем записать необходимые формулы и приступить к решению.
|
|
|
Результатом работы является Рабочая тетрадь с выполненными заданиями для самостоятельной работы, контрольными заданиями, которая сдается на проверку в электронном или печатном варианте.
Раздел 1. Теория пределов
В результате изучения раздела студент должен
знать:
¾ определение предела функции в точке;
¾ свойства предела функции в точке;
¾ формулы замечательных пределов;
¾ определение непрерывности функции в точке,
¾ свойства непрерывных функций;
уметь:
¾ вычислять пределы функций в точке и на бесконечности.
Предел последовательности
Определение предела последовательности
Определение. Если по некоторому закону каждому натуральному числу n поставлено в соответствие вполне определенное число ап, то говорят, что задана числовая последовательность 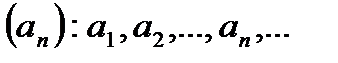
Т.е. числовая последовательность – это функция натурального аргумента: 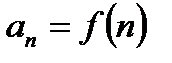 . Числа а1, а2,…,ап называются членами последовательности, а число ап – общим или п – м членом последовательности.
Определение. Последовательность (an) называется ограниченной, если существуют числа M и m такие, что для любого n выполняется неравенство: m £ (an) £ M. В противном случае она называется неограниченной. . Числа а1, а2,…,ап называются членами последовательности, а число ап – общим или п – м членом последовательности.
Определение. Последовательность (an) называется ограниченной, если существуют числа M и m такие, что для любого n выполняется неравенство: m £ (an) £ M. В противном случае она называется неограниченной.
|
Определение. Число А называется пределом последовательности (аn), если для каждого положительного числа e найдется такое натуральное число N, что для любого n > N справедливо неравенство:  . В этом случае пишут
. В этом случае пишут 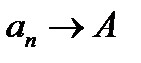 при
при  или
или 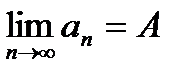
|
|
|
Определение. Последовательность (an), имеющая предел А, называется сходящейся к числу А, не имеющая предела последовательность называется расходящейся.
Геометрический смысл сходимости можно выявить, преобразовав выражение 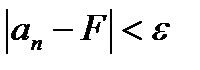 : : 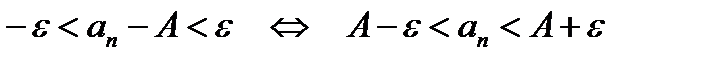
|
Таким образом, все члены последовательности (an), сходящейся к числу А, имеющие порядковые номера 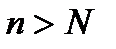 лежат в интервале (А– e; А + e), который называется e-окрестностью точки А.
лежат в интервале (А– e; А + e), который называется e-окрестностью точки А.
Величина  может стремиться к своему пределу различными способами:
может стремиться к своему пределу различными способами:
1) оставаясь меньше своего предела, 2) оставаясь больше своего предела, 3) колеблясь около своего предела и 4) принимая значения, равные своему пределу.
Пример. Докажем, что последовательность с общим членом 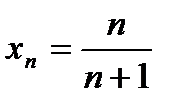 имеет предел, равный 1.
имеет предел, равный 1.
|
|
|
Решение.Выберем произвольно положительное число ε и покажем, что для него можно определить такое натуральное число N, что для всех номеров п > N будет выполняться неравенство, рассмотренное выше, в котором надо взять А = 1, т. е. неравенство
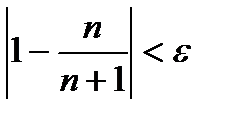
После приведения в скобках к общему знаменателю получим
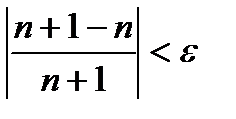 или
или 
Но если 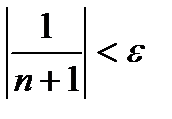 то и
то и 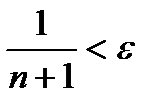 .
.
Из последнего неравенства следует, что 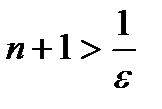 , а
, а  .
.
Значит, если номер N больше, чем 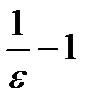 , то неравенство
, то неравенство 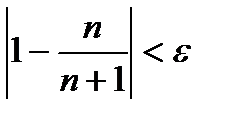 будет выполняться.
будет выполняться.
Теперь надо решить вопрос о числе N, о котором идет речь в определении. За число N можно принять наибольшее целое число, содержащееся в числе  . Наибольшее целое число, содержащееся в числе х, обозначается знаком Е (х). На основании этого наибольшее целое число, содержащееся в числе
. Наибольшее целое число, содержащееся в числе х, обозначается знаком Е (х). На основании этого наибольшее целое число, содержащееся в числе  надо обозначить так:
надо обозначить так: 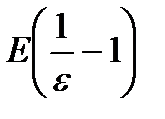 Итак, можно принять
Итак, можно принять 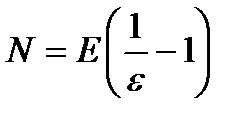 (предполагается, что
(предполагается, что 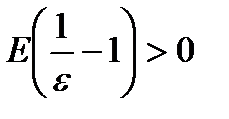 , иначе N не будет натуральным и его надо брать равным 1).
, иначе N не будет натуральным и его надо брать равным 1).
Таким образом, попроизвольно заданному положительному числу 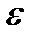 мы нашли такое натуральное число N, что для всех номеров n > N неравенство
мы нашли такое натуральное число N, что для всех номеров n > N неравенство 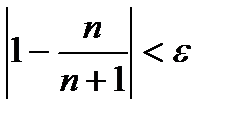 действительно выполняется, а этим и доказано, что 1 является пределом последовательности с общим членом
действительно выполняется, а этим и доказано, что 1 является пределом последовательности с общим членом 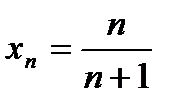 .
.
Проиллюстрируем это числовым примером.
Пусть, например, 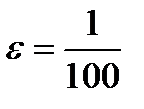 . Тогда при
. Тогда при 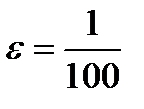 получаем из
получаем из 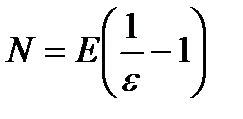 следующее значение:
следующее значение: 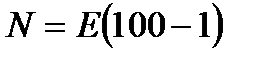 или
или 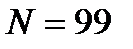
|
|
|
Таким образом, для членов последовательности с номером большим, чем 99, выполняется неравенство: 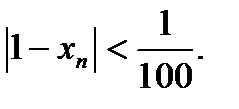
Пусть п = 97; тогда, так как 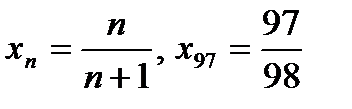 , то
, то  , а
, а 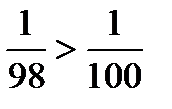
если п = 98, то 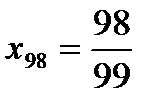 и
и 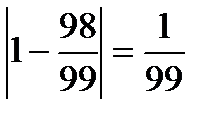 , а
, а 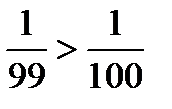
Из этих расчетов видно, что когда номер п члена последовательности меньше 99 неравенство 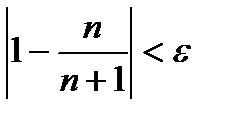 не выполняется, т.е.
не выполняется, т.е. 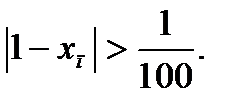 Если взять номер, превышающий 99, например, п = 101, то получим
Если взять номер, превышающий 99, например, п = 101, то получим 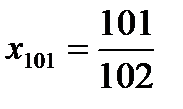 и
и 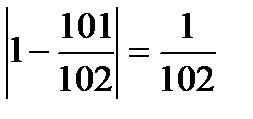 , а
, а 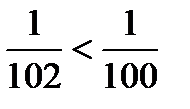 .
.
если п = 98, то 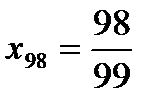 и
и 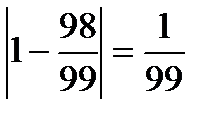 , а
, а 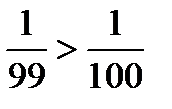
Полученный результат можно записать так: 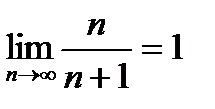 . Иначе можно сказать, что последовательность
. Иначе можно сказать, что последовательность 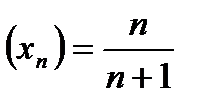 сходится к 1.
сходится к 1.
Мы употребили запись 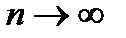 , которую следует понимать так: переменная величина п становится все большей и большей и не существует предела для ее возрастания. Какое бы большое число мы ни задали, п в процессе своего возрастания его превзойдет. Для того чтобы коротко описать этот характер изменения п, принято говорить «эн стремится к бесконечности» и записывать это так:
, которую следует понимать так: переменная величина п становится все большей и большей и не существует предела для ее возрастания. Какое бы большое число мы ни задали, п в процессе своего возрастания его превзойдет. Для того чтобы коротко описать этот характер изменения п, принято говорить «эн стремится к бесконечности» и записывать это так: 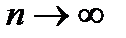 . Символ
. Символ 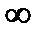 произносится «бесконечность» и применяется для сокращенной записи слова «бесконечность».
произносится «бесконечность» и применяется для сокращенной записи слова «бесконечность».
Символ 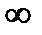 ни в коем случае не может рассматриваться как число, а потому бессмысленной является запись
ни в коем случае не может рассматриваться как число, а потому бессмысленной является запись 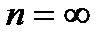 , так как п может равняться числу и не может быть равно символу, введенному только для сокращенной записи и сокращенного произношения фразы, которой заранее был придан определенный, указанный выше, смысл.
, так как п может равняться числу и не может быть равно символу, введенному только для сокращенной записи и сокращенного произношения фразы, которой заранее был придан определенный, указанный выше, смысл.
Очевидно, что последовательность 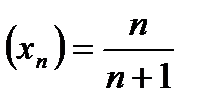 может быть записана таким образом:
может быть записана таким образом:
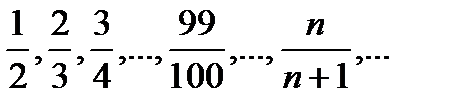
Пример. Докажем, что последовательность 3, З2, 33,34,..., 3" ... не имеет предела.
Решение. Мы докажем требуемое, если установим, что общий член этой последовательности  превзойдет любое наперед заданное число.
превзойдет любое наперед заданное число.
Пусть А такое число. Возьмем 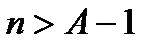 .
.
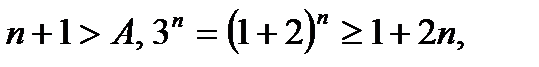 и подавно
и подавно 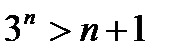 , или 3п > А. Тем самым показано, что 3п может превзойти любое число А. Если бы существовал предел переменной
, или 3п > А. Тем самым показано, что 3п может превзойти любое число А. Если бы существовал предел переменной 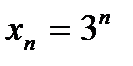 , и был бы равен А, то для любого
, и был бы равен А, то для любого 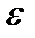 > 0 можно было бы подобрать такое N, что при номерах п > N выполнялись бы неравенства a
> 0 можно было бы подобрать такое N, что при номерах п > N выполнялись бы неравенства a 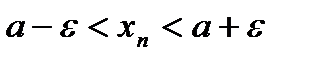 , т. е.
, т. е. 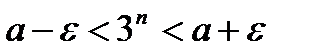 , а это противоречит доказанному, так как 3п при
, а это противоречит доказанному, так как 3п при 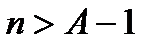 превзойдет любое число А, а тем самым и число a +
превзойдет любое число А, а тем самым и число a + 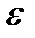 , меньше которого оно должно оставаться. Это противоречие и доказывает, что данная последовательность предела не имеет. Этот пример иллюстрирует утверждение: не всякая последовательность имеет предел.
, меньше которого оно должно оставаться. Это противоречие и доказывает, что данная последовательность предела не имеет. Этот пример иллюстрирует утверждение: не всякая последовательность имеет предел.
Свойства пределов последовательностей
Если две последовательности 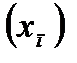 и
и 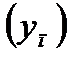 имеют пределы, равные соответственно А и В, то:
имеют пределы, равные соответственно А и В, то:
1) Последовательность 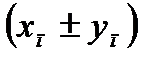 имеет предел, равный
имеет предел, равный 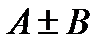 :
:

Это свойство распространяется на случай любого фиксированного числа слагаемых,
2) Последовательность 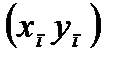 имеет предел, равный
имеет предел, равный 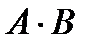 , т. е.
, т. е.
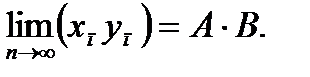
Это свойство распространяется также на случай любого фиксированного числа сомножителей.
Постоянный множитель можно выносить за знак предела:

при любом постоянном k.
3) Последовательность 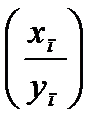 имеет предел, равный
имеет предел, равный 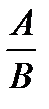 , т. е.
, т. е.
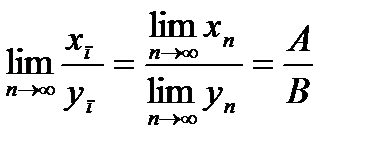 .
.
при условии, что все уп не равны нулю и 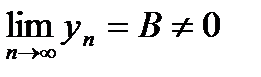 .
.
Пример. Найдем предел последовательности: 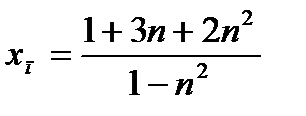 .
.
Решение. Очевидно, что числитель и знаменатель данной дроби имеют бесконечные пределы, т. е. представляют собой расходящиеся последовательности. Для разрешения проблемы произведем тождественное преобразование дроби, почленно разделив ее на наибольшую из степеней п (в данном случае, на 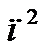 ). Предел полученной дроби найдем, определив значение предела каждого слагаемого в отдельности и учитывая, что
). Предел полученной дроби найдем, определив значение предела каждого слагаемого в отдельности и учитывая, что 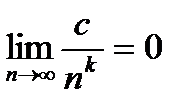 при условии, что с и k – постоянные, причем k больше 1. Помните, что предел постоянной величины есть сама величина, поскольку последовательность, все члены которой равны, имеет предел, равный ее общему члену. После этих подробных рассуждений укажем, как следует расположить записи:
при условии, что с и k – постоянные, причем k больше 1. Помните, что предел постоянной величины есть сама величина, поскольку последовательность, все члены которой равны, имеет предел, равный ее общему члену. После этих подробных рассуждений укажем, как следует расположить записи:
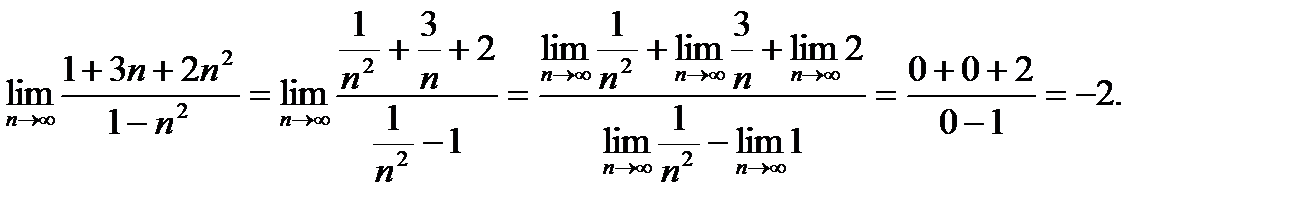
Здесь применена теорема о пределе дроби.
Ответ:–2.
Пример. Найдем 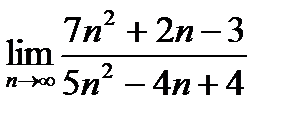 .
.
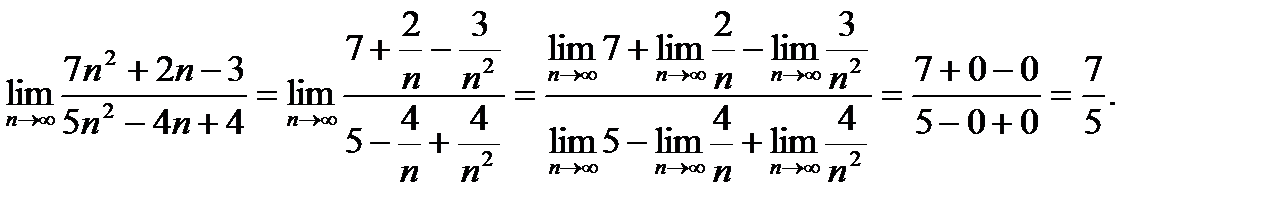
Ответ: 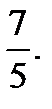
Задание. Вычислите предел последовательности:
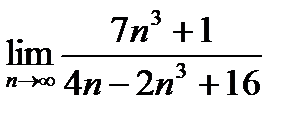
Решение:
__________________________________________________________________________________________________________________________________________________________

Ответ:
Предел функции
Определение предела функции в точке
Сформулируем определение предела функции в точке.
Определение. Пусть функция f( x) определена в некоторой окрестности точки а, кроме, может быть, самой точки а, Число В называется пределом функции f( x) в точке а (или при х, стремящемся к а), если для любой последовательности значений аргумента хп ¹ а, п Î N, сходящейся к а, последовательность соответствующих значений функции f( xп), п Î N, сходится к числу В.
В этом случае пишут: 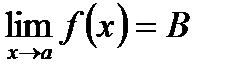 или
или 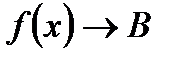 при
при 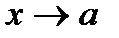 .
.
Если же для некоторой последовательности значений аргумента, сходящейся к а, соответствующая последовательность значений функции не является сходящейся, то функция в данной точке не имеет предела. То же заключение можно сделать, если для двух различных последовательностей значений аргумента последовательности соответствующих значений функции имеют различные пределы.
Очевидно, число В является пределом функции 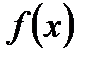 при
при 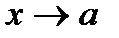 тогда и только тогда, когда
тогда и только тогда, когда 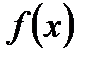 можно представить в виде:
можно представить в виде:
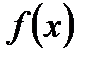 = В +
= В + 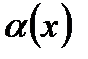 , где
, где 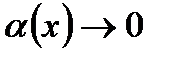 при
при 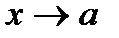 .
.
Отметим, что точка а, в которой рассматривается предел функции 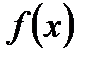 , может принадлежать области определения функции
, может принадлежать области определения функции 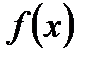 , а может и не принадлежать. При нахождении предела функции в точке не рассматривается значение функции в этой точке.
, а может и не принадлежать. При нахождении предела функции в точке не рассматривается значение функции в этой точке.
Пример. Докажем справедливость следующих равенств:
1)  , при
, при 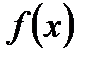 = с; 2)
= с; 2) 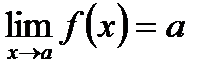 при
при 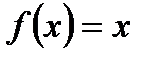 .
.
Решение.
1) Пусть 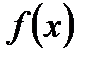 = с для всех х из некоторого интервала, содержащего точку а. Тогда для любой последовательности (х n) такой, что х n ® а при n ® ¥, имеем
= с для всех х из некоторого интервала, содержащего точку а. Тогда для любой последовательности (х n) такой, что х n ® а при n ® ¥, имеем 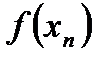 = с и
= с и 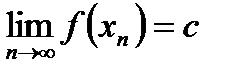 .
.
Следовательно 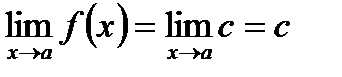 .
.
2) Для любой последовательности (х n) такой, что х n ® а при n ® ¥, имеем
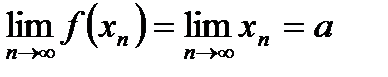 .
.
Следовательно, согласно определению предела 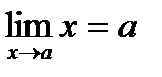 .
.
Свойства пределов функций
Основные свойства пределов функций аналогичны теоремам о пределах числовых последовательностей:
1) Предел суммы (разности) функций равен сумме (разности) их пределов, если последние существуют: 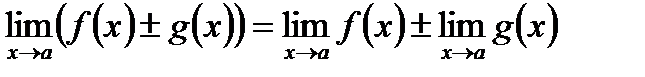 .
.
2) Предел произведения функций равен произведению их пределов, если последние существуют: 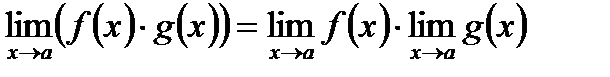 .
.
Следствие. Постоянный множитель можно выносить за знак предела: 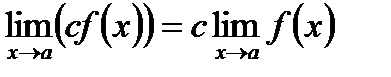 , если
, если 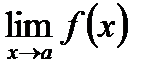 существует.
существует.
3) Предел отношения двух функций равен отношению их пределов, если последние существуют и предел делителя отличен от нуля: 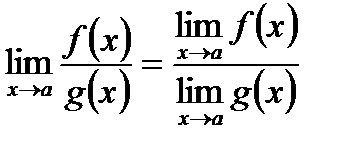 , если
, если 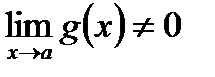 .
.
При изучении пределов функций иногда полезно использовать следующую «теорему о пределе промежуточной функции».
Теорема. Если 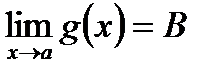 ,
,  и в некоторой окрестности точки а, кроме, быть может, самой точки а, выполняются неравенства
и в некоторой окрестности точки а, кроме, быть может, самой точки а, выполняются неравенства 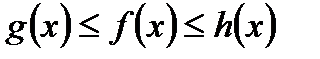 , то
, то 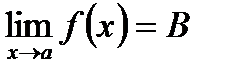 .
.
Пример. Вычислите пределы фукций: 1) 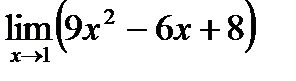 ; 2)
; 2) 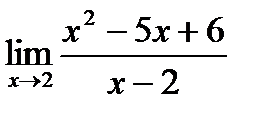 ; 3)
; 3) 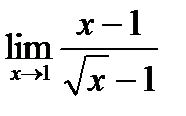 .
.
Решение.
1) 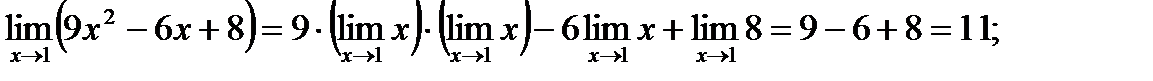
2) Поскольку предел знаменателя равен 0, то воспользоваться теоремой о пределе частного невозможно. Поэтому первоначально сократим дробь, разложив числитель на множители:
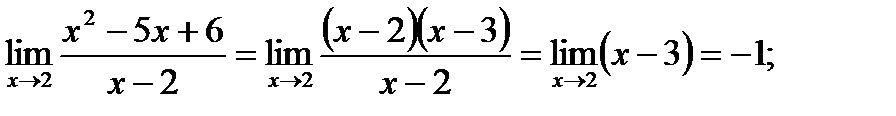
3)
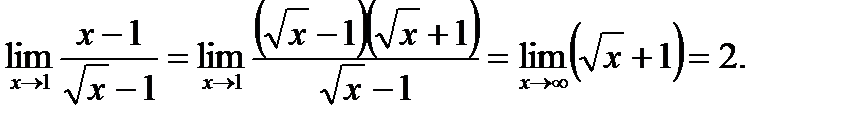
Ответ. 1) 11, 2) –1, 3) 2.
Задание. Вычислите пределы функций:
1). 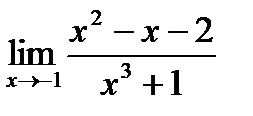
Решение:
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Ответ:-1
2). 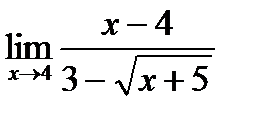
Решение:
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________Ответ:-6.
Определение предела функции на бесконечности
При изучении свойств функции приходится рассматривать предел функции в бесконечности, бесконечный предел функции в точке, а также бесконечный предел в бесконечности.
Рассмотрим более подробно предел функции в бесконечности, т.е. при 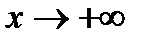 и при
и при 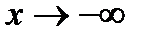 .
.
Определение. Пусть функция f( x) определена на всей числовой прямой. Число В называется пределом f( x) при 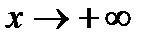 , если
, если 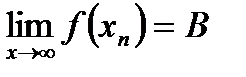 для любой последовательности (хп) такой, что
для любой последовательности (хп) такой, что 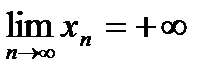 .
.
В этих случаях пишут, что 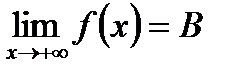 . Аналогично,
. Аналогично, 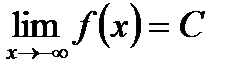 ,если
,если  для любой последовательности (хп) такой, что
для любой последовательности (хп) такой, что 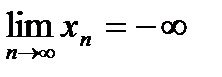 .
.
Пример. Докажем, что 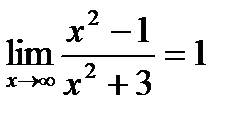
Решение.
Рассмотрим произвольную последовательность (хп) такую, что
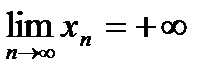 .
.
Так как последовательность 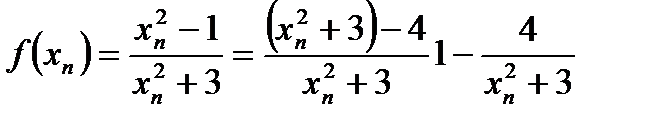 , где n Î N, сходится к 1, то согласно определению
, где n Î N, сходится к 1, то согласно определению 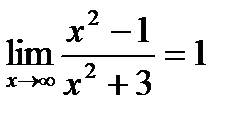 . Легко видеть, что и
. Легко видеть, что и 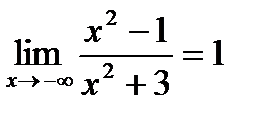 .
.
Кроме рассмотренного случая конечного предела функции f( x) при х ® ∞ (или иначе х ® ± ¥) используется понятие бесконечного предела. Например, функция  , определенная для всех х ¹ 0, принимает сколь угодно большие значения при х ® 0. В этом случае говорят, что функция в точке х = 0 имеет своим пределом бесконечность, и пишут
, определенная для всех х ¹ 0, принимает сколь угодно большие значения при х ® 0. В этом случае говорят, что функция в точке х = 0 имеет своим пределом бесконечность, и пишут 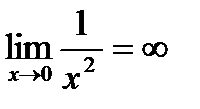 .
.
Определение. Если для любой последовательности значений аргумента (хп) такой, что хп ¹ 0 и 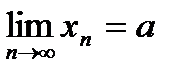 , имеет место
, имеет место 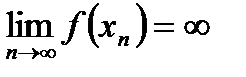 , то говорят, что предел функции f( x) в точке а есть бесконечность, и пишут
, то говорят, что предел функции f( x) в точке а есть бесконечность, и пишут 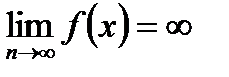 .
.
Пример. Найдите пределы функций:
1) 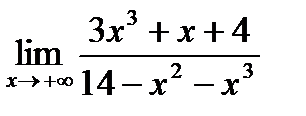 ; 2)
; 2) 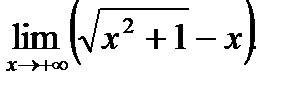
Решение. При определении значений предела функции на бесконечности воспользуемся тем же приемом, что и в случае последовательности:
1) 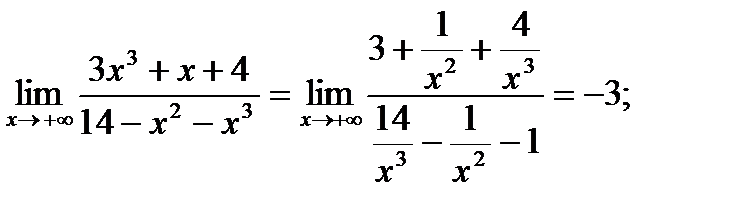
2)
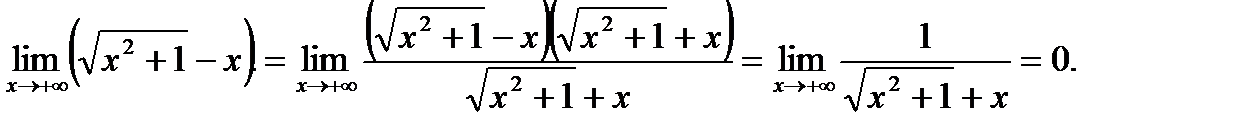
Ответ. 1) -3, 2) 0.
Задание. Вычислите предел функции на бесконечности:
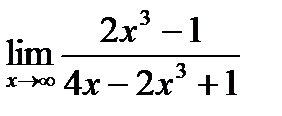
Решение:
____________________________________________________________________________________________________________________________________
Ответ:-1.
Дата добавления: 2019-01-14; просмотров: 232; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
