ПОСТРОЕНИЕ МОДЕЛЕЙ СИСТЕМ НА ОСНОВЕ МЕТОДА ПРОСТРАНСТВА СОСТОЯНИЙ
Как уже указывалось в гл.1, одним из фундаментальных понятий теории систем является понятие динамической системы. Это понятие в современной трактовке тесно связано с принципом причинности, который отражает одну из наиболее глубоких объективных закономерностей, присущих реальным явлениям окружающего нас мира. Динамическая система является наиболее общей абстрактной моделью реальных объектов, удовлетворяющих принципу причинности. В соответствии с правилами построения математических структур введем базисные множества, имеющие следующие наименования: T ={ t } - множество моментов времени, подмножество точек вещественной оси R ; U ={ u } - множество мгновенных входных ситуаций, характеризующих влияние среды на систему; Q ={ g } - множество состояний системы; x ={ x }- множество выходных ситуаций, характеризующее воздействие системы на среду.
Множества Q и X рассматриваются как основные, а Т и U -как вспомогательные базисные множества. Возможны несколько вариантов конструирования динамической системы в виде математической структуры, которые отличаются использованием различного числа ступеней шкалы множеств, строящейся на базисных множествах Т, U , Q , X, и различными схемами образования ступеней. К числу основных вариантов отнесем следующие: а) трехступенчатый, с типовыми характеристиками, заданными как элементы булеанов вида
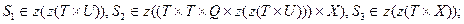
б) четырехступенчатый, с типовыми характеристиками:
|
|
|
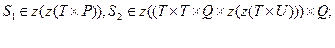
Отметим, что в этих вариантах указаны лишь основные ступени шкалы, на которых конструируется особый род математической структуры, которому принадлежат все динамические системы, рассматриваемые как математические объекты. При дальнейшем уточнении формального понятия динамической системы используются некоторые дополнительные ступени и соответствующая аксиоматика, определяющая строение указанной математической структуры. S 1 в варианте а) и б) связано с заданием множества входных воздействий, S 2 - собственно динамическая система, S 3 в а) и S 4 в б) определяют множество выходных процессов. Перейдем от абстрактного задания систем в смысле Н.Бурбаки к описанию систем, учитывающих их физическое состояние [1,14].
Состояния движение динамической системы
На первом этане уточним понятие состояния. Сделаем это примере уравнения простейшей электрической цепи (рис. 6.1).
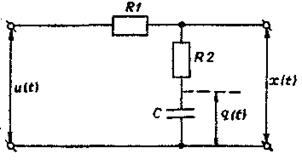
Рис. 6.1
Входной сигнал RC-цепи напряжение u ( t ), сигнал на выходе – напряжение .x ( t ). Входное сопротивление включенного далее элемента настолько велико, что нагрузка не оказывает влияния на x ( t ) Очевидно, что напряжение на выходе будет зависеть не только от напряжения на входе, но и от напряжения на конденсаторе при t=0. Поэтому рассмотрим напряжение на конденсаторе в качестве вспомогательной переменной q ( t ) и обозначим ее, поскольку она определяет начальное состояние RC-цепи как переменную состояния. По второму закону Кирхгофа получим i ( R 1 ,+ R 2 )+ q = u . Поскольку i = C  , T = C ( R 1 + R 2 ) то
, T = C ( R 1 + R 2 ) то  T + q =u. Сигнал на выходе x ( t )= q ( t )+( u ( t )- q ( t )) d , d = R 2 /( R 1 + R 2 ).
T + q =u. Сигнал на выходе x ( t )= q ( t )+( u ( t )- q ( t )) d , d = R 2 /( R 1 + R 2 ).
|
|
|
Если обозначить 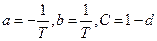 скалярные уравнения можно записать в так называемой стандартной форме. Уравнение состояния
скалярные уравнения можно записать в так называемой стандартной форме. Уравнение состояния  уравнение выхода
уравнение выхода 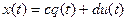 . Таким образом, переменная состояния
. Таким образом, переменная состояния 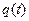 выражается дифференциальным уравнением первого порядка, так называемые уровнения состояния, а если известны переменная соотояния и сигнал на входе, то сигнал на выходе может быть найден с помощью алгебраического уравнения – уравнения выхода. Для решения уравнения состояния рассмотрим общее решение линейного уравнения:
выражается дифференциальным уравнением первого порядка, так называемые уровнения состояния, а если известны переменная соотояния и сигнал на входе, то сигнал на выходе может быть найден с помощью алгебраического уравнения – уравнения выхода. Для решения уравнения состояния рассмотрим общее решение линейного уравнения:
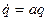 (6.1)
(6.1)
используя в качестве подстановки
q = kea t (6.2)
где величина k в соответствии с методом вариации произвольных постоянных переменна k = k ( t ) и вычисляется путем подстановки q и k в уравнение состояния:
|
|
|
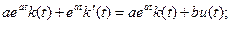 (6.3)
(6.3)
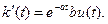 (6.4)
(6.4)
После интегрирования в пределах [0, t ]
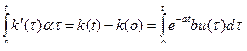 (6.5)
(6.5)
подстановки в уравнение (6.1) определяют
 (6.5)
(6.5)
Для t = 0 следует 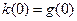 . Ели обозначить
. Ели обозначить
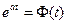 (6.7)
(6.7)
то искомое решение, которое и представляет собой уравнение движение системы первого порядка, имеет вид
 (6.8)
(6.8)
Первое слагаемое 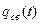 , которое зависит только от начальных условий g(o), определяет свободное, а второе q вын ( t ), которое зависит только от входного сигнала - вынужденное изменение переменной состояния q(t) [26].
, которое зависит только от начальных условий g(o), определяет свободное, а второе q вын ( t ), которое зависит только от входного сигнала - вынужденное изменение переменной состояния q(t) [26].
Исследуем реакцию RC – цепи на скачкообразное изменение входного напряжения:
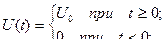
при начальном условии 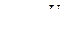 Определим свободную составляющую изменения состояния
Определим свободную составляющую изменения состояния 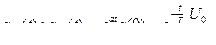 Свободная компонента напряжения на выходе при d = ½ будет хb(t) =(1–d) qсв(t)=
Свободная компонента напряжения на выходе при d = ½ будет хb(t) =(1–d) qсв(t)= 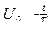 . Вынужденную составляющую изменения состояния находим следующим образом:
. Вынужденную составляющую изменения состояния находим следующим образом:  при
при 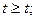
 при
при 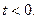 Вынужденную компоненту напряжения на выходе для
Вынужденную компоненту напряжения на выходе для 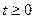 определяют (с учетом того, что
определяют (с учетом того, что 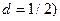 так:
так:
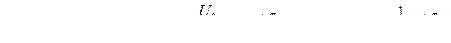
Суммирование свободного qc в ( t ) и вынужденного q вын ( t ) изменения переменной состояния g ( t ) и компонент x св ( t ) и x вын ( t) сигнала на выходе x ( t ) определяет полное изменение состояния q ( t )= q вын ( t )+ q вын ( t ) и напряжения на выходе x ( t ) = x вын ( t )+ x вын ( t ).
|
|
|
Рассмотрим систему с m входами и r выходами 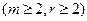 (рис.6.2). Для описания такой системы введем следующие переменные:
(рис.6.2). Для описания такой системы введем следующие переменные:
вектор входа (вектор входных сигналов) 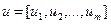 ′ (S1, в абстрактном толковании);
′ (S1, в абстрактном толковании);
вектор выхода x=[х1,хг1...1х] (S 3 , S 4 в абстрактном толковании);
вектор состояния (вектор сигналов состояния) q =[q 1 , q 2 ,…, qn]′ и его производную  .
.
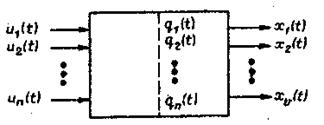
Рис. 6.2
Такая система описывается по n переменным состояния qi дифференциалъными уравнениями первого порядка и r алгебраическими уравнениями для определения r выходных сигналов xj
Итак, уравнениями многомерной системы называются: уравнение состояния (векторное дифференциальное уравнение)
 ( t )= Aq ( t )+ Bu ( t ); (6.9)
( t )= Aq ( t )+ Bu ( t ); (6.9)
уравнение выхода (векторное алгебраическое уравнение)
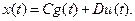 (6.10)
(6.10)
Вместо скалярных коэффициентов а, b ,с, d уравнений здесь фигурируют матрицы A , B , C , D, которые определяются следующим образом: A =( aij )-( n , n ) квадратная матрица системы, которая полностью определяет изменение состояния невозмущенной системы при  ; ( n , m ) – прямоугольная матрица управлений B =( bij ), которая описывает влияние управляющего вектора (вектора входа) на вектор состояния; (r , n) – матрица наблюдения (матрица выхода C =( Cij ), которая характеризует наблюдаемость внутреннего состояния посредством (доступного изменения) вектора выхода; ( r , m ) - переходная матрица D =( dij ), которая характеризует непосредственное, незадержанное влияние вектора входа на вектор выхода; в физических системах она обычно равна нулю. Для одномерной системы n -гo порядка эти уравнения упрощаются:
; ( n , m ) – прямоугольная матрица управлений B =( bij ), которая описывает влияние управляющего вектора (вектора входа) на вектор состояния; (r , n) – матрица наблюдения (матрица выхода C =( Cij ), которая характеризует наблюдаемость внутреннего состояния посредством (доступного изменения) вектора выхода; ( r , m ) - переходная матрица D =( dij ), которая характеризует непосредственное, незадержанное влияние вектора входа на вектор выхода; в физических системах она обычно равна нулю. Для одномерной системы n -гo порядка эти уравнения упрощаются:
уравнение состояния 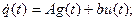 (6.11)
(6.11)
уравнение выхода 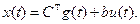 (6.I2)
(6.I2)
Поскольку x ( t ) и u ( t ) - скалярные функции, матрица А редуцируется в ( n ,1)-вектор столбец b , C - матрица С-в (1, r ) -вектор строку С' и матрица D - в скаляр b Для n =2
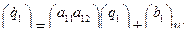 (6.13)
(6.13)
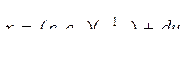 (6.14)
(6.14)
или 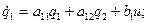
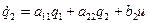 ;
;
и 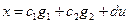
Рассмотрим пример (рис. 6.3).
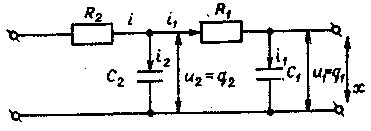
Рис. 6.3
Примем напряжения на конденсаторах u 1  и u 2 в качестве переменных состояния g 2 и g2 и заметим, что, поскольку i 1 = c 1
и u 2 в качестве переменных состояния g 2 и g2 и заметим, что, поскольку i 1 = c 1 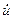 1= c 1
1= c 1  1 ; i 2 = c 2
1 ; i 2 = c 2 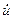 2= c 2
2= c 2  2 ; i = i 1 + i 2 уравнения для двух контуров имеют вид
2 ; i = i 1 + i 2 уравнения для двух контуров имеют вид
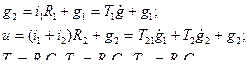
Для того, чтобы перейти к записи в стандартной форме, следует разрешить уравнения относительно производных переменных состояния, т.е. получить выражение.
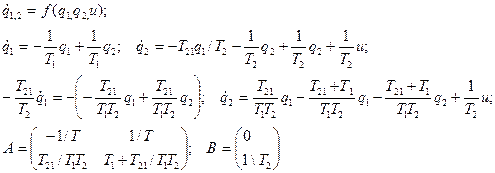
Уравнение выхода, поскольку сигнал на выхода совпадает с первой переменной состояния, имеет вид 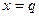 откуда
откуда 
Найдем уравнение движения для многомерной системы. Сменив в уравнении движения одномерной системы скалярные сигналы входа, выхода и состояния на векторы и соответственно скалярные коэффициенты a и в на матрицы А и В получим уравнение движения многомерной системы
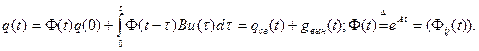
При n =2, m =1
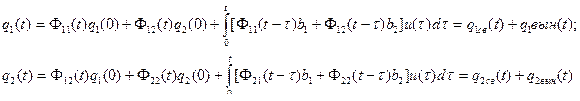
Дня многомерной системы высокого порядка изменение состояния для всех значений t > 0 может быть вычислено, если известны матрицы А и В (получаемые при выводе уравнений, системы), заданы начальное состояние g(0) и входной сигнал и 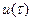 при
при 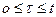 .
.
Вектор состояния 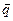 ( t ) образуется с помощью компонент gi ( t ), выбранных так и в таком количестве, что если известно их значение в .фиксированный (произвольный) момент времени t = 0, при заданном значении вектора входа
( t ) образуется с помощью компонент gi ( t ), выбранных так и в таком количестве, что если известно их значение в .фиксированный (произвольный) момент времени t = 0, при заданном значении вектора входа 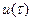 для
для  , то вектор выхода x ( t ) может быть определен однозначно.
, то вектор выхода x ( t ) может быть определен однозначно.
Компоненты gi называются переменными состояния. В качестве переменных состояния могут быть использованы различные физические переменные. В электрических цепях обычно рассматривают напряжения конденсаторов и токи индуктивностей. В экономических системах переменными состояния могут быть банки, сберкассы, торговые предприятия, биржа и т.д. Зачастую переменными состояния могут служить выходной сигнал и его производные до ( n -1)-й производной включительно.
В качестве исходного возьмем приведенное ниже дифференциальное уравнение n-го порядка:
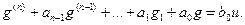 (6.16)
(6.16)
Путем замены переменных состояния q =  1
1 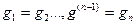 мы получим систему дифференциальных уравнений первого порядка [27]:
мы получим систему дифференциальных уравнений первого порядка [27]:
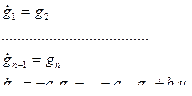 (6.17)
(6.17)
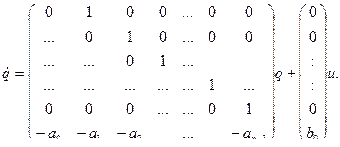 (6.18)
(6.18)
Матрица системы имеет так называемую форму Фробениуса и называется матрицей сопровождения. Она характеризуется тем, что элементы над главной диагональю являются единицами, а элементы нижней строки являются коэффициентами дифференциального уравнения. Все остальные элемента являются нулями [27, 29].
В самом общем случае для линейной системы n-го порядка с m входными параметрами и r выходными имеем следующую систему уравнений:
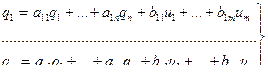 (6.19)
(6.19)
и
 (6.20)
(6.20)
В матричной форме (рис. 6.4).
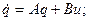 (6.21)
(6.21)
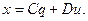 (6.22)
(6.22)
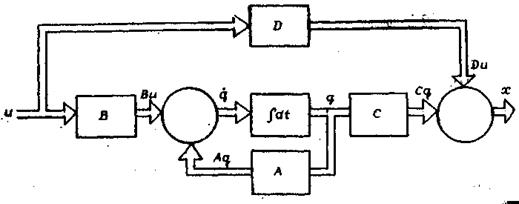
Рис. 6.4
Рассмотрим некоторые вспомогательные соотношения, которые позволят записать уравнения системы более просто. Вектор состояния может быть образован различными комбинациями переменных состояния. Определить их нужно в результате следующих преобразований. Рассмотри линейную систему, описываемую векторным уравнением состояния
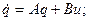 (6.23)
(6.23)
где 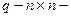 вектор состояния;
вектор состояния; 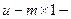 вектор возмущающих воздействий, или входной вектор, компоненты которого могут быть независимыми функциями времени; А, В – матрицы коэффициентов.
вектор возмущающих воздействий, или входной вектор, компоненты которого могут быть независимыми функциями времени; А, В – матрицы коэффициентов.
Для того чтобы построить вектор состояния различными способами, можно использовать линейное преобразование уравнения (6.23). Преобразование векторов состояния q*является линейной комбинацией n компонент вектора q.
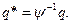 (6.24)
(6.24)
Уравнение (6.24) порождает новое уровнение состояния:
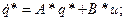 (6.25)
(6.25)
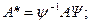 (6.26)
(6.26)
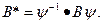 (6.27)
(6.27)
Указанное преобразование возможно только в том случае, когда существует матрица 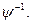 Заметим, что ни одна преобразованная переменная не может рассматриваться как переменная состояния, если она является линейной комбинацией одной или нескольких других переменных состояния. Собственные значения уравнения (6.23) совпадают с собственными значениями уравнения (6.24):
Заметим, что ни одна преобразованная переменная не может рассматриваться как переменная состояния, если она является линейной комбинацией одной или нескольких других переменных состояния. Собственные значения уравнения (6.23) совпадают с собственными значениями уравнения (6.24):
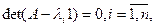 так как
так как 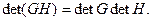 Получим
Получим


Среди множества различных линейных преобразований уравнения (6.23) особую роль играет каноническое преобразование, в котором матрицей преобразования является матрица собственных векторов V. Эта матрица получается из решения однородного линейного уравнения [29, 30]:
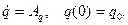 (6.28)
(6.28)
Решение имеет вид
 (6.29а)
(6.29а)
или в векторной форме
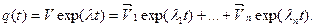 (6.29 б)
(6.29 б)
где


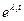
 …
… 
. . .
 . ; V = . … . =
. ; V = . … . = 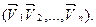 (6.30)
(6.30)
. . .

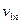 …
… 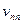
Для определения V нужно найти собственные векторы. Дифференцирова-нные (6.29б) по t дает
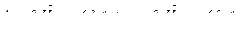 (6.31)
(6.31)
Подставляем (6.29 а) в (6.28), получаем
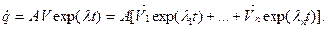 (6.32)
(6.32)
Сравнивая (6.31) и (6.32), находим, что собственные векторы 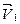 удовлетворяет (для случая, когда все
удовлетворяет (для случая, когда все 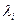 различны) соотношению
различны) соотношению
 (6.33)
(6.33)
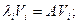 (6.34)
(6.34)
 (6.34а)
(6.34а)
Следовательно,  может быть определен из уровнения (6.34а).
может быть определен из уровнения (6.34а).
Рассмотрим пример:
 1 2
1 2
А = 4 3 ;

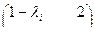 =
= 
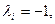

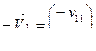 =
= 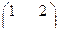
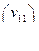 =
= 
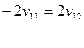 или
или 
Полагаем 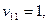 получаем
получаем 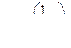 Аналогично соответствие с уровнением (6.34), (6.34а).
Аналогично соответствие с уровнением (6.34), (6.34а).
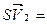
 =
= 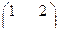
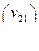 =
= 


Полагая 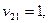 получаем
получаем
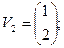
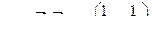
Применяя каноническое преобразование к уровнению (6.23), т.е. используя V как матрицу преобразования и учитывая (6.26), (6.27), получаем следующее канонические уровнения состояния:
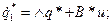
 (6.35)
(6.35)
или в скалярной форме:
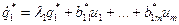
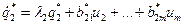
…………………………
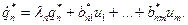 (6.36)
(6.36)
Следовательно, каноническое преобразование приводит к системе уравнений состояния, в которой каждая производная (канонической) переменой состояния зависит только от соответствующей (канонической) переменной состояния и от входных сигналов. Рассмотрим пример:
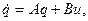
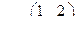 , В =
, В = 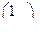
Каноническое преобразование матрицы А выполняется следующим образом: 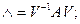
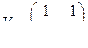 . Было получено в предыдущем примере.
. Было получено в предыдущем примере.
Тогда
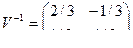 .
.

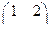
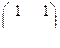 =
= 
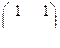 =
= 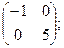
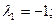
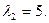
Поэтому диагональная матрица имеет вид 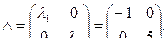
Дата добавления: 2018-11-24; просмотров: 306; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
