МАТЕМАТИЧЕСКАЯ ЛОГИКА. ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ И ПРЕДИКАТОВ

 

Функции алгебры логики и их основные свойства

 

Математическая логика – это анализ методов рассуждений. При этом исследуются формы рассуждений, а не их содержание. Формализа­ция рассуждений, ведущая начало от Аристотеля, приобрела современ­ный вид во второй половине 19-го в. в сочинении Джорджа Буля "Законы мысли". Наибольший расцвет математической логики начался в 50-е гг. 20-го в. в связи с бурным развитием цифровой техники. Учение о выска­зываниях, называемое алгеброй высказываний, является первой из фор­мальных логических теорий, и знакомство с законами алгебры высказы­ваний облегчает изучение исчисления высказываний и исчисления пре­дикатов. Кроме того, алгебра высказываний представляет самостоя­тельный интерес и имеет большое приложение при синтезе электронных схем [15, 16] .

Анализ рассуждений основывался на анализе так называемых логи­ческих функций, которые определяются путем задания области опреде­ления и области значения функций. Для этого рассмотрим набор < х₁, х₂,,.,,х_n>, в котором переменные x могут принимать значения 0 или 1 ("ложь "или "истина"). При этом количество различных числовых на­боров такого вида равно 2ⁿ . Функция, определенная на таких наборах и принимающая в качестве своих значений на этих наборах 0 или 1, на­зывается функцией алгебра логики (ФАЛ), или булевой функцией. Так как число различных наборов является конечным, то любая ФАЛ может быть полностью задана конечной таблицей с 2ⁿ строками. Переменные х₁, х₂,,.,,х_n называются аргументами функции алгебры логики. 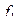Если две функции  и принимают на всех 2ⁿ наборах одинаковые значения, то функции  и  считаются равными. При этом функции алгебры логики могут не зависеть от некоторых элементов набора 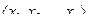 Функция  существенно зависит от аргумента , если имеет место соотношение

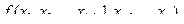
В противном случае говорят, что функция несущественно зависит от аргумента . Функция, в которой какому-то аргументу  придано значение 0 или 1, называется соответственно нулевой или единичной остаточной функцией. Они в этом случае являются функциями от n – 1 аргументов. Нетрудно показать, что существует 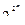различных функ­ций от n аргументов (табл.4.1). В этой таблице справа записана од­на из функций алгебры логики, зависящая от n аргументов. Задавая тот или иной конкретный двоичный набор 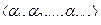, мы бу­дем задавать одну из возможных функций алгебры логики. Число набо­ров 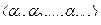равно числу 2ⁿ разрядных двоичных чисел, т.е. .В число  функций алгебры логики входят как функции, существенно зависящие от всех n аргументов, так и функции, для ко­торых часть из этих аргументов являются фиктивными. Например, для n =1 имеем =4 различные функции (табл.4.2).

В этом случае только функци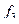и  и 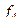 существенно зависят от x₁, а для функци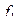й  и  этот единственный аргумент является фиктивным. Число всех функций алгебры логики, существенно завися­щих от n аргументов, определяется следующим рекуррентным соотноше­нием [16]:

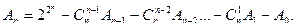                                                     (4.2)

В этом соотношении А_i есть число ФАЛ, существенно зависящих от i аргументов. Из последнего примера следует, что А₀ = 2, А₁ = 2. Тог­да . Рассмот­рение множества элементарных функций алгебры логики начнем со слу­чая n = 0. Имеются только две функции, совпадающие с константами 0 и 1:

Таблица 4.1

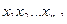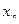
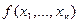
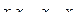
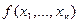
0 0 … 0 0		…………………	.
0 0 … 0 1		…………………	.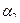
0 0 … 1 0		1 1 … 1 1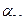

 

Таблица 4.2

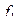
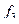
0	0	1	0	1
1	0	1	1	0

 

Таблица 4.3

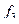
0	0	1
1	1	0

 

В случае n = 1 имеем две функции, существенно зависящие от одно­го аргумента. Они определяются табл. 4.3.

Эти две функции обозначим 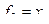 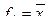Функция 4 называет­ся отрицанием. Читается "не х". Построим все булевы функции от двух переменных (табл. 4.4).

Из этих шестнадцати функций, как было показано, существенно зависящих от двух аргументов, будет лишь десять функций, из кото­рых семь являются существенно различными и имеют важное значение при построении логических схем. Нетрудно видеть, что введенные функ­ции 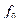– это функция 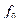– константа нуль;  – это функция  – константа единица; 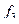 – это функция 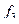согласно табл. 4.3 – пе­ременная х₁ (аналогично 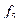);  – это функция 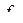 (отрицание х₁), аналогично  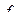– отрицание х₂.

Семь существенно зависящих от двух аргументов функций имеют следующие названия:

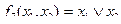 – функция дизъюнкции или логического сло­жения (в табл. 4. 4 это функция );

 – функция конъюнкции (в табл. 4.4 это функция );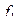

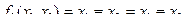 – функция равнозначности (эквива­лентности) (в табл.4.4 это функция );

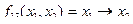 – функция импликации х₁ в х₂. Читается «если х₁, то х₂» (в табл. 4.4 это  аналогично

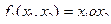– функция Вебба (отрицание дизъюнкции: в табл. 4.4 это функция );

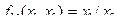– функция Шеферра (отрицательные конъюнкции; в табл. 4.4 это функция );

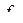– функция сложения по модулю два.

Таблица 4.4

х1	х2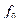
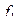
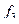
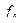
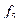
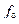
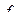
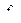
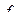
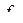
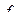
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

 

Таблицы типа табл. 4.3 и 4.4, задающее значения функций на всех возможных наборах, называется таблицами истинности. Рассмотренные одиннадцать функций позволяют строить новые функции алгебры логики путем:

– перенумерации аргументов;

– подстановки в функцию новых функций вместо аргументов.
Используя таблицы истинности, определяющие элементарные функции, можно задавать в виде таблицы истинности любую ФАЛ, являющуюся суперпозицицией этих функций. Пусть требуется представить в виде таблицы функцию:

Будем строить функцию последовательно (табл.4.5).

Таблица 4.5

х1	х2	х3				[ ]		{ }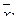
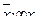
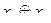
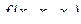
0	0	0	1	0	1	1	0	0	1
0	0	1	1	1	1	1	0	0	1
0	1	0	1	0	0	0	1	0	1
0	1	1	1	1	0	1	1	1	1
1	0	0	0	1	0	1	1	1	0
1	0	1	0	0	0	0	1	0	1
1	1	0	0	1	0	1	0	0	1
1	1	1	0	0	0	0	0	0	1

Таблицы истинности можно использовать для проверки равенстве или неравентсва различных ФАЛ. Рассмотрим отдельным важные примеры (табл. 4.6 – 4.11).

 

Таблицы 4.6                                      Таблицы 4.7

                        

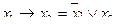
х1	х2
0	0	1
0	1	1
1	0	0
1	1	1

х1	х2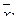
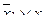
0	0	1	1
0	1	1	1
1	0	0	0
1	1	0	1

     

Таблицы 4.8                                      Таблицы 4.9

                            

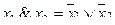
Х1	х2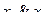
0	0	0
0	1	0
1	0	0
1	1	1

х1	х2
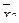
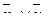
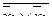
0	0	1	1	1	0
0	1	1	0	1	0
1	0	0	1	1	0
1	1	0	0	0	1

 

 

Таблицы 4.10                                      Таблицы 4.11

                        

х1	х2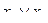
0	0	0
0	1	1
1	0	1
1	1	1

х1	х2
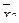
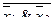
0	0	1	1	1	0
0	1	1	0	0	1
1	0	0	1	0	1
1	1	0	0	0	1

      

 

Последние две формулы носят название формул де Моргана и могут быть обобщены:

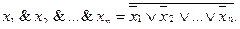
Особую роль в развитии методов синтеза электронных схем сыграли функции 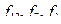 – соответственно отрицания, дизъюнкции и конъюнкции. Поэтому отдельно остановимся на их свойствах. Функция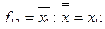  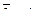Функции дизъюнкции и конъюнкции обладают рядом свойств, аналогичны свойствам обычных операций умножения и сложения. Для этих функций справедливы сочетательный:

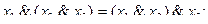
переместительный

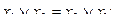
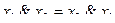
и распределительный законы конъюнкции относительно дизъюнкции:

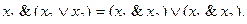                               (4.5)

Кроме того, имеет место распределительный закон дизъюнкции относительно конъюнкции:

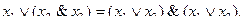                           (4.6)

который не имеет места в обычной алгебре, так как если бы он существовал, то имел бы вид

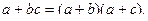
Справедливость распределительного закона дизъюнкции относительно конъюнкции легко устанавливается путем построения таблиц истинность для правой и левой частей формулы, отражающей этот закон.

Все введенные функции, кроме аналитической записи, имеют и содержательный смысл. Верно и обратное: любое сложное высказывание можно записать в виде функции от простых высказываний. Например, рассмотрим высказывание: "Если две стороны одного треугольника и угол между ними равны соответственно двум сторонам другого треуголъника и углу между ними, то такие треугольники равны". Это высказывание легко расчленить на следующие три высказывания: "Две стороны одного треугольника равны соответственно двум сторонам другого треугольника", "Угол, заключенный между этими сторонами одного треугольника, равен соответствующему углу другого треугольника". "Такие треугольники равны". Если обозначить: х₁ – первое высказывание; х₂ – второе высказывание;  – третье высказывание), то получим связь истинности и ложности этих высказываний в виде таблицы истинности:

Таблица 4.12

х1	х2
0	0	0
0	1	0
1	0	0
1	1	1

 

Нетрудно видеть, что это есть таблица истинности для функции 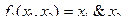– функции конъюнкции: если х₁ и х₂, то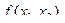  

Очевидно, что и другие более сложные высказывания могут быть записаны в виде формул алгебры логики через введенные ранее функ­ции 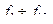 При этом встают вопросы о различных аналитических вы­ражениях высказываний и их минимальном (наиболее экономном с точ­ки зрения количества входящих символов и их числа) представлении. С этой целью разобьем все множество функций алгебры логики на клас­сы и сформулируем одну из основных теорем, отвечающую на вопрос о количестве необходимых функций для полного описания высказываний.

 

---

Дата добавления: 2018-11-24; просмотров: 269; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!