Разбиения и расстояния на графах
Рассмотрим вопрос разбиения ребер, дуг или вершин графа ни множества определенного структурного типа и введем дополнительную характеристику – расстояние, определяемое через длину дуги (ребра) Все эти вопросы связаны с дискретными оптимизационными задачами. Начнем с разбиения ребер графа на наименьшее число непересекающихся подмножеств, каждое из которых является либо цепью, либо циклом (не обязательно простым). Разбиения такого типа назовем реберным разделением [10, II], а состоящие из наименьшего возможного числа цепей и циклов будут называться минимальными реберными разделениями. Заметим, что каждое отдельное ребро графа является цепью или в случае петли циклом. Следовательно, каждый граф имеет реберное разделение. Очевидно также, что для конечных графов всегда существует минимальное реберное разделение. При этом изолированные вершины не влияют на вид реберного разделения. Минимальное реберное разделение для несвязного графа может быть получено путем нахождения минимального реберного разделения отдельно для каждой компоненты, имеющей ребра. С учетом этого без потери общности будем рассматривать только связные графы. Особый интерес представляют графы, реберные разделения которых являются единственной цепью или циклом т.е. графы, совокупность ребер которых образует цепь или цикл. Такие графы называют уникурсальными, поскольку здесь существует возможность непрерывного прохождения всех ребер, без повторения какого-либо ребра. Свойства минимальных реберных разделений существенно зависят от наличия в графе вершин нечетной степени. (И, как было показано ранее, число вершин нечетной степени всегда четно.) Графы, не обязательно связные, все вершины которых имеют четную степень, называются эйлеровыми графами. Минимальные реберные разделения для связных эйлеров графов определяются следующей теоремой.
|
|
|
Теорема. Если G =(V,E) – связный эйлеров граф, то E является циклом, образующим единственное минимальное реберное разделение, покрывающее граф G.
Доказательство. Если граф содержит петли, то удалим их и рассмотрим полученный таким образом новый граф, все вершины которого сохраняют четную степень. Начнем движение с любой вершины v1 по некоторому ребру к другой граничной точке ребра, скажем v2. Так как вершина v2 имеет четную степень, то она инцидентна второму ребру, которое приводит нас к вершине v3. Продолжая такой процесс обхода, мы всегда дойдем до вершины 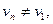 так как четность всех вершин гарантирует, что в любом случае мы можем покинуть любую вершину, используя ребро, отличное от того, по которому пришли в эту вершину. Так как число ребер конечно, то в результате для некоторого n мы имеем vn= v1. Пройденные ребра образуют цикл. Если при этом оказалось, что пройдены все ребра, то теорема доказана. В противном случае удалим полученный цикл и рассмотрим оставшийся подграф. Каждая вершина этого подграфа имеет четную степень, и, следовательно, мы можем повторить предыдущее построение, найти и удалить второй цикл. За конечное число шагов удаление очередного цикла приведет к тому, что в подграфе не останется ребер. Полученное множество циклов вместе с удаленными вначале петлями образует реберное разделение графа G. А так как G связен, то объединение этих циклов, т.е. ним является циклом. Цикл, который покрывает граф, называется эйлеровым циклом (рис.3.22).
так как четность всех вершин гарантирует, что в любом случае мы можем покинуть любую вершину, используя ребро, отличное от того, по которому пришли в эту вершину. Так как число ребер конечно, то в результате для некоторого n мы имеем vn= v1. Пройденные ребра образуют цикл. Если при этом оказалось, что пройдены все ребра, то теорема доказана. В противном случае удалим полученный цикл и рассмотрим оставшийся подграф. Каждая вершина этого подграфа имеет четную степень, и, следовательно, мы можем повторить предыдущее построение, найти и удалить второй цикл. За конечное число шагов удаление очередного цикла приведет к тому, что в подграфе не останется ребер. Полученное множество циклов вместе с удаленными вначале петлями образует реберное разделение графа G. А так как G связен, то объединение этих циклов, т.е. ним является циклом. Цикл, который покрывает граф, называется эйлеровым циклом (рис.3.22).
|
|
|
В отличие от полученного результата минимальные реберные разделения связных графов, имеющих вершины нечетной степени, состоят только из цепей. Для этого случая имеются два утверждения, которые легко доказываются.
Связный граф G = (V, Е), содержащий 2 n вершин нечетной степени, где n≥1, имеет минимальное реберное разделение, состоящее из цепей, каждая из которых соединяет две вершины нечетной степени. Из рассмотренной теоремы и последнего утверждения непосредственно следует, что связный граф является уникурсальным тогда и только тогда, когда он имеет 0 или точно 2 вершины нечетной степени. В первом случае он покрывается циклом, в последнем – цепью, соединяющей две вершины нечетной степени.
|
|
|
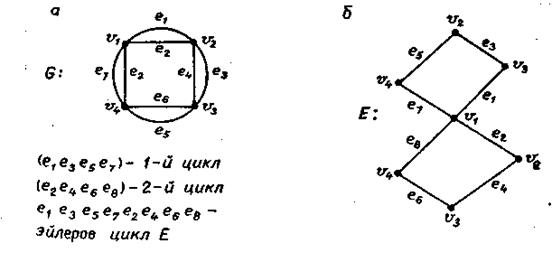
Рис. 3.22
Классической задачей, имеющей отношение к уникурсальным графам, является задача о кенигсбергских мостах, которая возникла в свази с прогулкой горожан по городу. Вопрос состоял в том, можно ли совершить прогулку таким образом, чтобы, выйдя из дома, вернуться обратно, пройдя только один раз по каждому из семи мостов, связывающих части города, расположенного на берегах реки Прегель и двух островах. Предположим, что v1 и v2 обозначают оба берега реки, a v3 и v4 - острова, тогда граф на рис.3.23 показывает, каким образом мосты связывают части города.
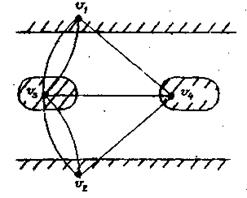
Задача была сформулирована Л.Эйлером в 1736 г. в следующем виде: определить, существует ли непрерывный маршрут, который проходит по каждому мосту точно один раз, другими словами, является ли граф, показанный на рис.3.23,.уникурсальным. Так как все четыре вершины имеют нечетную степень, то граф не является уникурсальным, и требуется, по крайней мере, две цепи для того, чтобы покрывать этот граф. На рис.3.24 показаны два минимальных реберных разделения. (В обоих случаях одна из цепей показана штриховой линией, а другие - сплошной.)
|
|
|
Для ориентированного графа Д=(V, A) разобьем вершины на непересекающиеся множества:
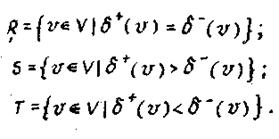
| 
|
| Рис. 3.23 | Рис. 3.24 |
Ориентированный граф называется равновесным по вершине v, если 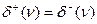 . Ориентированный граф, который является равновесным по каждой вершине, называется ориентированным эйлеровым графом. В этом случае имеет место R=V, и если граф связен, то множество А образует контур и является минимальным (единственным) реберным разделением.
. Ориентированный граф, который является равновесным по каждой вершине, называется ориентированным эйлеровым графом. В этом случае имеет место R=V, и если граф связен, то множество А образует контур и является минимальным (единственным) реберным разделением.
Если ориентированный граф Д=(V, A) связен, но не является равновесным, то всякое минимальное реберное разделение Д состоит из k путей, каждый из которых соединяет вершину из S с вершиной из Т. При этом
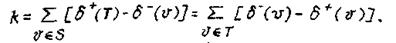 (3.7)
(3.7)
Ориентированный связный граф Д=(V, A) является уникурсальным тогда и только тогда, когда он является либо ориентированным эйлеровым графом, либо таким, что |S|=|T| и 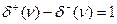 для единственной вершины v
для единственной вершины v 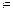 S.Последние два утверждения используются при описании потоков в сетях. К вопросу уникурсальности близкой является следующая:
S.Последние два утверждения используются при описании потоков в сетях. К вопросу уникурсальности близкой является следующая:
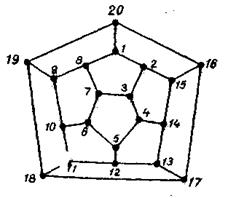
Задача [10, 12]: найти, при каких условиях конечный связный граф содержит цепь или цикл, проходящий через все вершины. Если такие цепь или цикл существуют и являются простыми, то они называются соответственно гамильтоновой цепью или гамильтоновым циклом. Название цикла и цепи связано с работами знаменитого математика Вильяма Гамильтона, придумавшего деловую игру (рис.3.25) в 1859 г.
Играющий должен обойти "вокруг света", найдя такой замкнутый путь, идущий по ребрам многогранника, который проходил бы через каждую вершину один раз.
| 
|
| Рис. 3.25 | Рис. 3.26 |
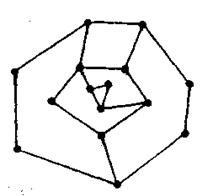
В настоящее время не известно эффективных описаний гамилътоновых графов (граф, имеющий остовный гамильтоновый цикл), но известно несколько необходимых и достаточных условий существования гамилътоновых циклов. Для этого введем понятие тэта-графа. Тэта-графом называется блок, содержащий только вершины степени 2 и две несмежные вершины степени 3. Таким образом, тэта-граф состоит из двух вершин степени 3 и трех непересекающихся простых цепей, соединяющих эти вершины, причем длина каждой из этих цепей не меньше 2. Имеет место
Теорема. Каждый гамильтонов граф двусвязен. Каждый негамильтонов двусвязный граф содержит тэта-подграфы [11, 13].
На рис. 3.26 легко найти тэта-подграфы в негамильтоновом блоке.
Достаточное условие, что граф гамильтонов, дают теоремы Поша [11, 12] и Дирака [11, 12].
Теорема Поша. Пусть G имеет 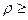 3 вершин. Если для всякого n,
3 вершин. Если для всякого n, 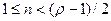 число вершин со степенями, не превосходящими n, меньше чем n, и для нечетного
число вершин со степенями, не превосходящими n, меньше чем n, и для нечетного 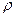 число вершин степени (
число вершин степени ( 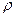 -1)/2 не превосходит
-1)/2 не превосходит 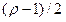 , то G - гамильтонов граф.
, то G - гамильтонов граф.
Приведенное достаточное условие не является необходимым.
Теорема Дирака. Если граф G=(Y,Е), 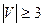 , является связным и степень каждой вершины
, является связным и степень каждой вершины 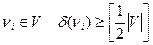 , где [ ] - ближайшее целое число, то граф является гамильтоновым [13].
, где [ ] - ближайшее целое число, то граф является гамильтоновым [13].
Понятия гамильтоновых цепей и циклов могут быть непосредственно обобщены на случай ориентированных графов.
Простой путь или контур, который проходит через все вершины графа, называется соответственно гамильтоновым путем или гамильтоновым контуром. Гамильтоновы пути и контуры в ориентированном графе определяют гамильтоновы цепи и циклы в соответствующем неориентированном графе. Они, кроме всего прочего, требуют определенной ориентации дуг; поэтому появление их в графах будет еще более редким. В отличие от обыкновенного полного ориентированного графа, который имеет множество гамильтоновых циклов, полный антисимметрический граф может и не иметь гамильтоновых контуров. Например, если в графе сушествует вершина v, для которой 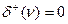 или
или 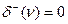 , то в таком графе не могут существовать гамильтоновы контуры.
, то в таком графе не могут существовать гамильтоновы контуры.
Ориентированный граф называется тотальным, если каждая пар различных вершин соединяется, по крайней мере в одном направлении контуром. Необходимым и достаточным условием того, что ориентированный граф без контуров содержит в точности один гамильтонов путь является тотальность графа. Интересной задачей, связанной с поиском кратчайшего гамильтонова контура, является задача.коммивояжера. Коммивояжер должен посетить по одному разу каждый из n городов (каждая пара городов связана дорогой) и вернуться в исходный город. При этом он должен выбрать кратчайший маршрут. Таким образом, мы пришли к необходимости ввести еще одну характеристику множества дуг-вес, длину, стоимость. Очевидно, что определение кратчайшего маршрута с помощью просмотра всех гамильтоновых циклов приводит к перебору  возможных циклов, и эта величина является астрономической для больших n. Необходимо найти эффективный алгоритм решения этой задачи. Такого алгоритма до сих пор не существует [13]. Вычислительные алгоритмы, предложенные для решения задачи коммивояжера, приведены в работе [13].
возможных циклов, и эта величина является астрономической для больших n. Необходимо найти эффективный алгоритм решения этой задачи. Такого алгоритма до сих пор не существует [13]. Вычислительные алгоритмы, предложенные для решения задачи коммивояжера, приведены в работе [13].
Рассмотрим подход [13], позволяющий свести сложную задачу нахождения кратчайшего гамильтонова цикла к просмотру возможных, которые находятся в более простых подграфах. Будем предполагать, что рассматриваемый граф является плоским и обыкновенный плоский граф имеет, по крайней мере, одну вершину степени 5 или меньше. Кроме того, предполагается также, что длины ребер выражаются положительными числами. Начиная с произвольной вершины v1, минимальной степени 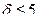 можно определить
можно определить 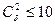 различных подграфов, каждый из которых состоит из всех вершин исходного графа, всех ребер, не инцидентных c v1, и двух из
различных подграфов, каждый из которых состоит из всех вершин исходного графа, всех ребер, не инцидентных c v1, и двух из 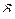 ребер, инцидентных v1. Таким образом, задача нахождения всех гамильтоновых циклов исходного графа свелась к задачам нахождения гамильтоновых циклов в
ребер, инцидентных v1. Таким образом, задача нахождения всех гамильтоновых циклов исходного графа свелась к задачам нахождения гамильтоновых циклов в 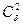 полученных подграфах, каждый из которых содержит вершину v1 степени 2.
полученных подграфах, каждый из которых содержит вершину v1 степени 2.
Рассмотрим один из подграфов 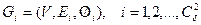 . Выберем вершину v1 степени 2. Начиная с ребра е1, инцидентного v1, и смежной вершины наименьшей степени (если обе смежные вершины одной степени, то выбираем любую), строим гамильтонов цикл Сn из последовательности n простых цепей Ck=(e1, …, ek), где ej≈(vj & vj+1) для j=1, …, k, помня при этом, что vn+1
. Выберем вершину v1 степени 2. Начиная с ребра е1, инцидентного v1, и смежной вершины наименьшей степени (если обе смежные вершины одной степени, то выбираем любую), строим гамильтонов цикл Сn из последовательности n простых цепей Ck=(e1, …, ek), где ej≈(vj & vj+1) для j=1, …, k, помня при этом, что vn+1 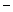 v1. (Это обозначение подразумевает, что ребра и вершины помечаются в той последовательности, в какой они встречаются при построении.) Ребро ek может присоединяться к Сk-1, если выполняются следующие условия:
v1. (Это обозначение подразумевает, что ребра и вершины помечаются в той последовательности, в какой они встречаются при построении.) Ребро ek может присоединяться к Сk-1, если выполняются следующие условия:
1) 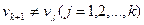 , eсли
, eсли 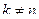
2) 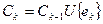 не разделяет оставшийся граф в том смысле, что любые две вершины
не разделяет оставшийся граф в том смысле, что любые две вершины 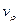 ,
, 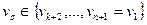 могут быть связаны цепью из рёбер, нe инцидентных ни одной вершине {v2, v3, …, vk+1}. Если несколько ребер удовлетворяют условиям добавления к цепи в одной и той же вершине, то выбирается ребро наименьшей длины, а остальные ребра запоминаются. Если ни одно ребро не удовлетворяет условиям 1 и 2 и не может быть присоединено к конечной вершине vk+1 цепи Ck, (k<n), то такая цепь не является частью гамильтонова цикла и отбрасывается. При этом производится возврат в последнюю вершину произвольного выбранного ребра и исследуется новая цепь. Когда описанный процесс закончится, все существующие в Gi гамильтоновы циклы будут найдены. Если применим эту процедуру для всех подграфов, то найдем все гамильтоновы циклы исходного графа. Пусть Si - длина кратчайшего ребра в i-м подграфе (т.е.
могут быть связаны цепью из рёбер, нe инцидентных ни одной вершине {v2, v3, …, vk+1}. Если несколько ребер удовлетворяют условиям добавления к цепи в одной и той же вершине, то выбирается ребро наименьшей длины, а остальные ребра запоминаются. Если ни одно ребро не удовлетворяет условиям 1 и 2 и не может быть присоединено к конечной вершине vk+1 цепи Ck, (k<n), то такая цепь не является частью гамильтонова цикла и отбрасывается. При этом производится возврат в последнюю вершину произвольного выбранного ребра и исследуется новая цепь. Когда описанный процесс закончится, все существующие в Gi гамильтоновы циклы будут найдены. Если применим эту процедуру для всех подграфов, то найдем все гамильтоновы циклы исходного графа. Пусть Si - длина кратчайшего ребра в i-м подграфе (т.е. 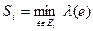 , где λ - функция расстояния, определенная на Е). После того как найден первый гамильтонов цикл Сn (в любом подграфе), можно вычислить его длину |Сn|. Пусть С
, где λ - функция расстояния, определенная на Е). После того как найден первый гамильтонов цикл Сn (в любом подграфе), можно вычислить его длину |Сn|. Пусть С 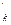 обозначает некоторую часть строящейся цепи в i-м подграфе длиной |С
обозначает некоторую часть строящейся цепи в i-м подграфе длиной |С 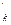 |. Для того чтобы С
|. Для того чтобы С 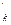 вошла в гамильтонов цикл С длиной меньше Сn, необходимо обеспечить |С
вошла в гамильтонов цикл С длиной меньше Сn, необходимо обеспечить |С 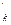 |+(n-k)Si<|Сn| на каждом шаге описанной процедуры. Поясним метод на примере графа G (рис. 3.27), где цифры указывают длину ребер. На рис. 3.28 показаны три подграфа, полученные при определенном выборе v1 и соответствующих значениях Si.
|+(n-k)Si<|Сn| на каждом шаге описанной процедуры. Поясним метод на примере графа G (рис. 3.27), где цифры указывают длину ребер. На рис. 3.28 показаны три подграфа, полученные при определенном выборе v1 и соответствующих значениях Si.
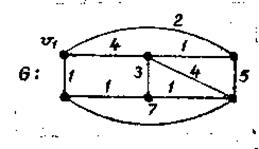
Рис. 3.27
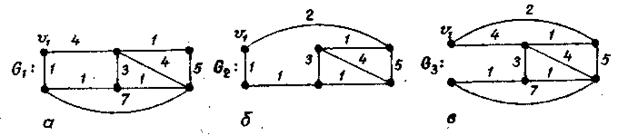
Рис. 3.28
На рис. 3.29 показана последовательность шагов, требуемых для построения первого гамильтонова цикла в G. Ребра, показанные жирными линиями, являются ребрами цикла.
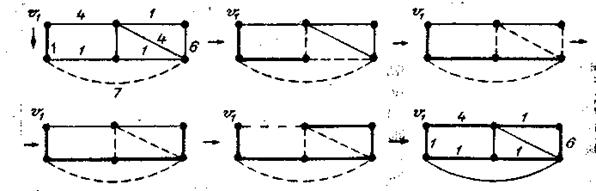
Рис. 3.29
Условие 2 данного метода эквивалентно требованию того, чтобы граф, полученный из G1, удалением жирных и штриховых линий (на каждом шаге) был связен. Длина гамильтонова цикла для G, равна 13. Проделав аналогичные шаги для подграфов G2 и G3, найдем,что кратчайший гамильтонов цикл будет для подграфа G2 (длина равна 10). Его вид приведен на рис.3.30.
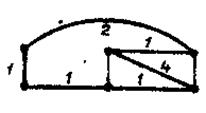
Рис. 3.30
Рассматриваемый метод иллюстрирует смысловую сторону нахождения гамильтонова цикла и решение задачи коммивояжера и хорошо работает для небольших графов; Реализация метода на ЭВМ затруднена проверкой условия 2. Обычно на ЭВМ она решается методом ветвей и границ. Для графа может быть поставлена не только задача нахождения минимального гамильтонова цикла. Не менее важной задачей является задача наикратчайшего маршрута между любыми двумя произвольными вершинами. Эта задача имеет более широкое 'применение в сетевых моделях, теории кодирования, исследовании моделей производственных систем [10] и обычно именуется как задача о кратчайшем пути и формулируется следующим образом.
Дан неориентированный граф G=(V,E). Каждому ребру этого графа приписано некоторое число L(e)  0, называемое длиной ребра. В частных случаях L(e) может быть расстоянием между вершинами, соединяемыми ребром е, временем или стоимостью проезда по этому ребру и т.п. При этом любая цепь μ будет характеризоватьcя длиной, определяемой следующей формулой:
0, называемое длиной ребра. В частных случаях L(e) может быть расстоянием между вершинами, соединяемыми ребром е, временем или стоимостью проезда по этому ребру и т.п. При этом любая цепь μ будет характеризоватьcя длиной, определяемой следующей формулой:
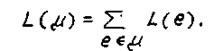 (3.8)
(3.8)
Рассмотрим вначале наиболее простой случай нахождения кратчайшего пути в графе с ребрами единичной длины. При решении этой задачи используем метод индексов [10, 14]. Поясним его на примере графа для задачи о ханойской башне (рис.3.31).
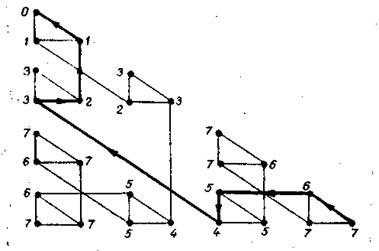
Рис. 3.31
Общее правило для нахождения кратчайшего пути в графе состоит в том, чтобы каждой вершине vi приписать индекс λi, равный длине кратчайшего пути из данной вершины в конечную (за начальную и ко нечную выбираются вершины, кратчайшее расстояние между которыми необходимо найти).
Приписывание индексов вершинам в случае графа с ребрами единичной длины производится в слвдунцем порядке:
- конечной вершине v0 приписывается индекс 0;
- всем вершинам, из которых идет ребро в конечную вершину,приписывается индекс 1;
- всем вершинам, еще не имеющим индексов, из которых идет реб'ро в вершину с индексом λi, приписывается индекс λi+1.
Процесс продолжается до тех пор, пока не будет помечена вершина, до которой ищется минимальное расстояние от v0, причем индекс этой вершины будет длиной кратчайшего пути. Сам кратчайший путь найдем, если будем двигаться из начальной вершины в направлении убывания индексов (рис.3.31).
Описанный способ определения кратчайшего пути является частным случаем нахождения оптимального решения по методу динамического пpoграммирования [10, 14]. Задача приписывания вершинам графа числовых индексов усложняется, если ребра графа имеют произвольную длину. Усложнение вызвано тем, что в сложном графе путь, проходящий через наименьшее число вершин, нередко имеет большую длину, чем некоторые обходные пути. Так, в графе (рис.3.32) прямой путь из вершины (10) в конечную имеет длину 12, а обходной - через вершину (9) имеет длину 10. Процесс приписывания индексов для такого вида графов заключается в следующем [12, 14]:
- каждая вершина vi помечается индексом λi. Первоначально конечной вершине v0 приписывается индекс λ0. Для остальных вершин предварительно полагаем λi=∞ (i≠0);
- ищем такое ребро (vi, vj), для которого vj-λi>l(vi, vj), и заменяем индекс λj индексом λ 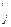 =λj+l(vi, vj)<λj. Продолжаем процесс замены индексов до тех пор, пока останется хотя бы одна дуга, для которой можно уменьшить λj.
=λj+l(vi, vj)<λj. Продолжаем процесс замены индексов до тех пор, пока останется хотя бы одна дуга, для которой можно уменьшить λj.
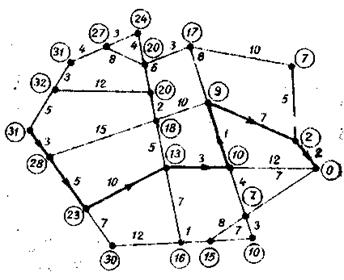
Рис. 3.32
Отметим два свойства, которыми будут обладать приписанные вершинам индексы:
- пусть (vk, vS) - произвольное ребро. Для него обязательно выполняется условие 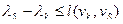 , так как, если бы оно не выполнялось, индекс λS можно было бы уменьшить;
, так как, если бы оно не выполнялось, индекс λS можно было бы уменьшить;
- пусть  - произвольная вершина. При рассмотренном процессе приписывания индексов индекс
- произвольная вершина. При рассмотренном процессе приписывания индексов индекс 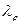 монотонно уменьшается. Пусть vq - последняя вершина, послужившая для его уменьшения. Тогда
монотонно уменьшается. Пусть vq - последняя вершина, послужившая для его уменьшения. Тогда 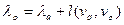 . Следовательно, для произвольной вершины
. Следовательно, для произвольной вершины 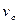 с индексом
с индексом 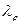 найдется вершина vq, соединенная ребром с
найдется вершина vq, соединенная ребром с  , такая, что
, такая, что 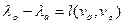 .
.
Эти свойства позволяют сформулировать следующее правило для нахождения кратчайшего пути.
Пусть vn=а - начальная вершина с индексом vn. Ищем вершину 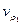 такую, что
такую, что 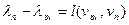 . Далее ищем вершину
. Далее ищем вершину 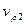 , такую, что
, такую, что 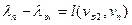 и т.д. до тех пор, пока не дойдем до конечной вершины
и т.д. до тех пор, пока не дойдем до конечной вершины 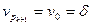 . Пусть
. Пусть 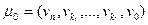 , длина которого
, длина которого 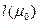 является кратчайшей.
является кратчайшей.
Для доказательства рассмотрим произвольный путь из а в b; 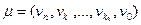 . Его длина будет
. Его длина будет 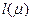 . Согласно правилу расстановки индексов будут выполняться следующие неравенства:
. Согласно правилу расстановки индексов будут выполняться следующие неравенства:
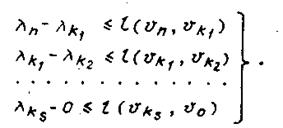
Складывая - почленно эти неравенства, находим, что для любого пути μ имеет место 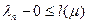 . Так как для пути
. Так как для пути 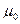 выполняется условие
выполняется условие 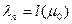 , то путь
, то путь 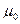 является кратчайшим.
является кратчайшим.
Метод нахождения кратчайшего пути проиллюстрирован на примере карты дорог, представленной в виде графа на рис.3.32. Цифры у ребер указывают время проезда по каждой из дорог. Индексы вершин дают время проезда от данной вершины до конечной.
С вопросами расстояний на графе тесно связаны понятия радиуса и диаметра графа, в частности о понятием диаметра связано одно из важных понятий графов – матрица достижимости, которая определяет все цепи между любой парой вершин. Если обозначить 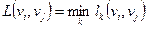 расстояние между вершинами vi и vj, где
расстояние между вершинами vi и vj, где 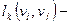 число ребер цепи, соединяющей vi и vj, то максимальное расстояние между вершинами графа G называется диаметром графа d (G):
число ребер цепи, соединяющей vi и vj, то максимальное расстояние между вершинами графа G называется диаметром графа d (G):
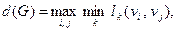
Матрица смежности графа может быть построена различными способами. Рассмотрим один из них, предварительно присвоив названия ребрам, а вершины обозначим числами натурального ряда. Решим эту задачу для графа Питерсона (рис. 3.33):

Рис. 3.33
Матрица смежности S определяет цепи единичной длины. Для цепей длиной n необходимо матрицу смежности Sn возвести в n-ю степень. При атом элемент матрицы Sn представляет множество цепей длиной n, описываемых идентификаторами ребер, входящих в цепи, соединяющие вершины vi и vj. При возведении в n-ю степень матрицы смежности S = (Si j) (Si j – множество идентификаторов ребер, соединяющих вершины vi, vj; sij = 0, если вершины не смежны) умножение рассматриваем как конкатенацию – приписывание справа к идентификатору, соответствующему i-й строке, идентификатора, соответcтвующему i-му столбцу, суммирование – как теоретико-множественное объединение полученных в результате умножения слов. Для примера найдем все цепи длиной 2 в ранее рассмотренном графе Питерсона. С этой целью возведем матрицу S в квадрат (см. ниже).

| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |

| e | k | 1 | |||||||

| b | m | 2 | |||||||
| b | c | n | 3 | |||||||
| c | d | p | 4 | |||||||
| е | d | r | 5 | |||||||
| k | s | x | 6 | |||||||
| m | t | y | 7 | |||||||
| n | u | 8 | ||||||||
| p | x | t | 9 | |||||||
| r | y | u | 10 |
S =

| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 
| 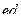
| 
| 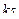
| 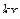
| 
| 1 | |||
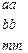
| 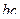
| 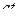
| 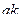
| m | 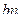
| 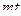
| 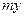
| 2 | ||
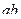
| 
| 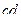
| 
| 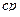
| 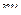
| 3 | ||||
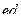
| 
| 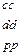
| 
| 
| 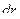
| 4 | ||||
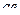
| 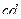
| 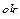
| 
| 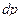
| 5 | |||||
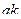
| 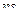
| 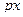
| 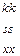
| 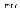
| 6 | |||||

| 
| 
| 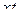
| 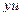
| 7 | |||||
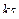
| 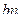
| 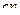
| 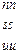
| 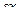
| 8 | |||||
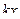
| 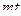
| 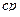
| t | 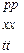
| 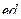
| 9 | ||||

| 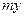
| 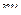
| 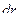
| r | 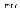
| 
| 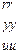
| 10 |
S =
Суммируя матрицы 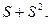 получаем, что в результирующей матрице отсутствуют нулевые элементы, что означает существованиние цепи длиной І или 2 между любой парой вершин графа Питерсона; а это означает, что параметр графа d (G) = 2.
получаем, что в результирующей матрице отсутствуют нулевые элементы, что означает существованиние цепи длиной І или 2 между любой парой вершин графа Питерсона; а это означает, что параметр графа d (G) = 2.
Следовательно, граф Питерсона связный и представляет собой ком-понентную связность. Если граф имеет k компонент связанности, то его матрицы достижимости, под которой понимается выражение
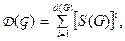 (3.10)
(3.10)
где d (G) – диаметр графа (G); S(G) – матрицы смежность, является k-клеточной, имеет вид

A1 0
A2
Д (G) = . (3.11)
.
.
0 Ak
Здесь матрицы A1, A2, …, Aк не содержат ни одного нулевого элемента (кроме, быть может, диагональных). Матрица достижимости содержит информацию о всех цепях, соединяющих любую пару вершин в графе, и используется при построении сетевых графиков планирования работ [13].
Для ориентированных графов было введено понятие сильной связности. Граф G сильно связен, если любая пара вершин соединена путем. Максимальный по включению вершин сильно связный подграф графа называется его компонентой сильной связности. Граф называется несильно связным, если число его компонент сильной связности больше единицы. Для определения компонент сильной связности максимальная степень, в которую необходимо возвести матрицу смежности графа S(G),равна диаметру этого графа. Компоненте сильной связности в матрице достижимости соответствует подматрица максимального размера, каждый элемент которой не равен нулю.
Дальнейшее изучение возможностей задания структурных свойств систем с помощью графов связано с вопросами разбиения вершин, из которого вытекают основные теоремы о раскраске вершин и ребер графа.
Множество вершин называется независимым, если оно не содержит двух смежных вершин. В частности, изолированная вершина образует независимое множество. Для получения независимого множества можно начать его построение с произвольной вершины и добавить к нему последовательно другие по условию несмежности с уже выбранными вершинами. Такой процесс может закончиться нахождением максимального независимого множества. Однако у нас не может быть полной уверенности в том, что W будет наибольшим из всех возможных независимых множеств, так как объем W зависит от того, какие вершины выбираются на каждом шаге процесса. В качестве предельного случая рассмотрим граф, показанный на рис. 3.34. Если начнем процесс выбора с любой вершины, отличной от v1, и на каждом шаге выбираем любую вершину, кроме v1, то в конце концов получим максимальное независимое множество Wr, которое включает все вершины графа, кроме одной. С другой стороны, если нам не повезло и мы выбрали на первом шаге v1, то в результате получится максимальное независимое множество W2 ,состоящее из единствен-ной вершины. Максимальное независимое множество обладает свойством доминирования в графе в том смысле, что каждая вершина графа является либо элементом W, либо смежна с элементом W. Действительно, если какое-то независимое множество не доминирует в графе, то существует, по крайней мере, одна вершина, не принадлежащая множеству W и не смежная о ним. Такую вершину можно включать в множество W, не нарушая его свойств. Таким образом, исходное множество не было максимальным. Множество вершин, обладающее свойством доминирования, называется доминирующим множеством, вне зависимости от того, является оно независимым или нет. (В неориентированном графе понятие доминирующего множества соответствует понятию внешне устойчивого множества. В ориентированном графе понятию внешне устойчивого множества соответствует понятие обратного доминирующего множества.) Введем основные инварианты графа для попарно несмежных вершин и попарно несмежных ребер. В соответствии с введенными понятиями будем считать множество вершин внутренне устойчивым, если они попарно несмежны. Внутренне устойчивое множество вершин называется пустым подграфом, если добавление хотя бы одной вершины, не принадлежащей этому множеству, образует хотя бы одно ребро (дугу). Максимальная мощность пустого подграфа графа G называется числом внутренней устойчивости, или вершинным числом независимости графа 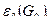 Максимальное число попарно несмежных ребер графа G называется реберным числом независимости графа
Максимальное число попарно несмежных ребер графа G называется реберным числом независимости графа 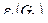

Рис. 3.34
Если ребро инцидентно вершине, то говорят, что они покрывают друг друга. Множество вершин, покрывающих все ребра графе, называется вершинным покрытием графа G .
Минимальная мощность вершинного покрытия называется числам вершинного покрытия графа 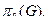 Аналогично множество ребер, покры-вающих все вершины графы G, называетсяпокрыттям графа. Минимальная мощность реберного покрытия графа G называется числом реберного покрытия
Аналогично множество ребер, покры-вающих все вершины графы G, называетсяпокрыттям графа. Минимальная мощность реберного покрытия графа G называется числом реберного покрытия 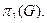 Условимся считать, что любая вершина графа покрывает сама себя и две смежные вершины покрывают друг друга. Тогда минимальная мощность множества вершин, покрывающих все вершины графа G, называется вершинным числом внешней устойчивости графа β0 (G).
Условимся считать, что любая вершина графа покрывает сама себя и две смежные вершины покрывают друг друга. Тогда минимальная мощность множества вершин, покрывающих все вершины графа G, называется вершинным числом внешней устойчивости графа β0 (G).
Аналогично будем считать, что каждое ребро графа покрывает себя и два смежных ребра покрывают друг друга; тогда минимальная мощность множества ребер, покрывающих все ребра графа G, называется реберным числом внешней устойчивости β1 (G). Вычисление рассмотренных инвариантов графа требуется при решении многих практических задач [I3].
Пусть, например, вершины графа представляют собой технологические модули гибкого автоматизированного производства, за которыми должно осуществляться непрерывное наблюдение, а две вершины графа соединены ребром, если соответствующие им модули можно наблюдать, находясь около одного из них. Требуется так расставить телекамеры, чтобы оператор, находящийся у монитора на диспетчерском пульте, мог наблюдать за всеми модулями, но при этом число телекамер было бы минимальным.
Для решения этой задачи надо определить вершинное число внешней устойчивости данного графа. Так, например, введенные инварианты для графа Петерсона (см. рис. 3.33) имеют следующие значения: 
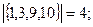
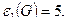
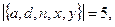

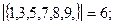
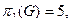
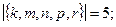
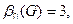
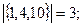
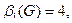
 Для любого нетривиального связного графа G = (V, E).
Для любого нетривиального связного графа G = (V, E).  Алгоритмы нахождения инвериантов графа приведены в [13].
Алгоритмы нахождения инвериантов графа приведены в [13].
В обыкновенном графе G вершина v доминирует над собой и над  вершинами, с которыми она смежна. Следовательно, множество из k вершин
вершинами, с которыми она смежна. Следовательно, множество из k вершин  доминирует самое большее над
доминирует самое большее над 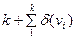 вершинами. Если граф содержит n вершин, то необходимым условием того, что S будет внешне устойчивым множествам, является
вершинами. Если граф содержит n вершин, то необходимым условием того, что S будет внешне устойчивым множествам, является
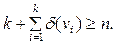 (3.12)
(3.12)
В частности, внешне устойчивое множество для обыкновенного графа, который является р-однородным, должно содержать по меньшей мере n/(p+1) вершин. С рассмотренными задачами тесно связан один класс задач, который является предметом многих исследований.
Требуется разделить вершины данного графа на наименьшее число независимых множеств. Задачи подобного типа называются задачами раскраске и формулируются следующим образом: назначить каждой вершине цвет (или абстрактную метку) таким образом, чтобы смежные вершины всегда имели различные цвета (пометки) и число различных используемых цветов (пометок) было как можно меньше. Это наименьшее число называется хроматическим числом графа. Хроматическое число обыкновенного графа G, имеющего n вершин, меньше чем n, если граф G неполный, и больше 1, если G вообще содержит какие-нибудь ребра.
Для отдельных классов графов хроматическое число находится путем элементарных рассуждений. Например, каждое дерево (исключая вырожденное дерево, состоящее из одной изолированной вершины) имеет хроматическое число, равное двум. Следует отметить тесную связь между хроматическим числом графа и понятием k-дольного графа. Хроматическое число G является просто наименьшим k, при котором G является k-дольным (дерево является двудольным графом).
Дадим строгое определение раскраски вершин графа, которое сводится в конечном итоге к нахождению наименьшего числа независимых множеств, на которые разбивается множество вершин.
Раскраской вершин графа G = (V, E) в 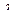 цветов называется разбиение носителя V графа G, при котором каждое подмножество Vі(
цветов называется разбиение носителя V графа G, при котором каждое подмножество Vі( 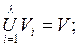
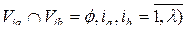 не содержит ни одной пары смежных вершин. Каждому подмножеству сопоставляется цвет, в который окрешивают все элементы подмножества. Хроматическим числом h (G)графа G называется минимальное число
не содержит ни одной пары смежных вершин. Каждому подмножеству сопоставляется цвет, в который окрешивают все элементы подмножества. Хроматическим числом h (G)графа G называется минимальное число 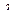 , для которого граф имеет
, для которого граф имеет 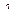 раскраску. Возникают две задачи: первая – найти
раскраску. Возникают две задачи: первая – найти 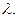 вторая – найти число правильных раскрасок графа (граф называется правильно раскрашенным
вторая – найти число правильных раскрасок графа (граф называется правильно раскрашенным 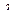 красками, если каждая вершина раскрашена одной из
красками, если каждая вершина раскрашена одной из 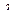 красок и если (v1 & v2)
красок и если (v1 & v2) 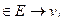 и
и  раскрашены разными красками).
раскрашены разными красками).
В общем случае, если граф плоский, то имеется гипотеза о четырех красках (которая не доказана и не опровергнута), которая утверждает, что для плоского графа 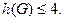 Для отдельных классов графов имеются более точные теоремы, например.
Для отдельных классов графов имеются более точные теоремы, например.
Теорема Кенига. Граф является 2-хроматическим тогда и только тогда, когда он не содержит циклов нечетной длины [11 – 13].
Хроматическое число графа может быть оценено через его параметры (степень вершин и вершинное число независимости графа). Если максимальная степень вершин графа G равна 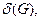 то хроматическое число этого графа не превышает величины
то хроматическое число этого графа не превышает величины 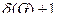 т.е.
т.е. 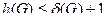 Для любого графа G = (V, E).
Для любого графа G = (V, E).
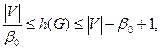
где  вершинное число независимости графа.
вершинное число независимости графа.
Аналогично вводится раскраска ребер. Подсчет числа правильных раскрасок графа G 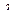 красками представляет собой сложную комбинаторную задачу. Для графа G, имеющего |V| вершин и |Е| ребер, имеет место следующее утверждение.
красками представляет собой сложную комбинаторную задачу. Для графа G, имеющего |V| вершин и |Е| ребер, имеет место следующее утверждение.
Теорема. Число правильных раскрасок 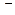 (G,
(G, 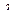 ) графа G
) графа G 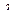 красками равно
красками равно 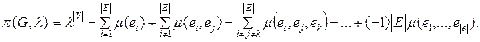 Здесь
Здесь 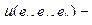 число неправильных раскрасок, где ребра
число неправильных раскрасок, где ребра 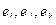 раскрашены неверно. Теорема доказывается на основе метода включения и исключения и носит чисто теоретическое значение, так как не дает практического способа подсчета числа правильных раскрасок. Для небольших графов G (V,E) имеет место следующая формула числа правильных раскрасок:
раскрашены неверно. Теорема доказывается на основе метода включения и исключения и носит чисто теоретическое значение, так как не дает практического способа подсчета числа правильных раскрасок. Для небольших графов G (V,E) имеет место следующая формула числа правильных раскрасок:
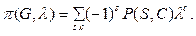 (3.14)
(3.14)
Здесь Р(S,С) – число подграфов графа G, имеющих "С" компонент связности и S ребер; 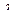 – число красок,
– число красок,
Пример (рис. 3.35). Дан граф G(V,Е). Рассмотрим все случаи сочетания S и С. Определим P(S, С) : Р (0,3) = I, P (1,2) =3, Р (2,1) = 3, Р (3,1) = 1:
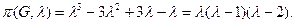

Рис. 3.35
Хроматический полином равен нулю при 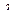 = 1,
= 1, 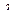 = 2, При
= 2, При 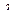 = 3 =
= 3 =  число правильных раскрасок равно
число правильных раскрасок равно 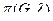 = 3 ∙ 2 ∙ 1 = 6. Для облегчения подсчета числа правильных раскрасок графа G обычно задачу разбивают на более простыв. Основой для такого упрощения служат следующие леммы.
= 3 ∙ 2 ∙ 1 = 6. Для облегчения подсчета числа правильных раскрасок графа G обычно задачу разбивают на более простыв. Основой для такого упрощения служат следующие леммы.
Лемма 1. Если графы G1, и G2 не связаны (представляют компоненты связности графа G), то
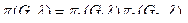 (3.15)
(3.15)
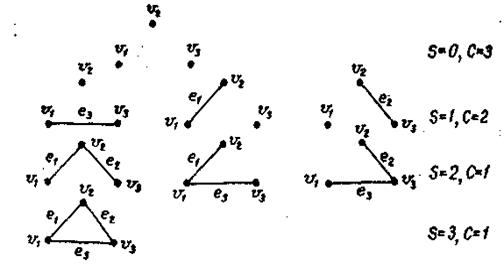
Рис. 3.36
Лемма 2. Если граф G имеет точку сочленения v0 (см. рис.3.37), то
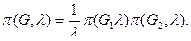 (3.16)
(3.16)
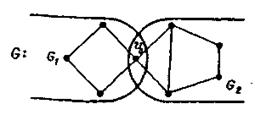
Рис. 3.37
Лемма 3. Если граф G имеет мост l (см. рис.3. 38) , то
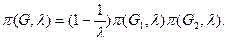 (3.17)
(3.17)
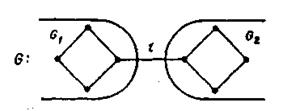
Рис. 3.38
Лемма 4. Если граф G получен из графа G1 добавлением ребра t без изменения числа вершин, то
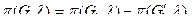 (3.18)
(3.18)
где граф 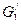 получен из G1 склеиванием висячей вершины инцидентной ребру l , и преобразованием полученого графа в простой граф – объединение параллельных ребер (рис. 3.39).
получен из G1 склеиванием висячей вершины инцидентной ребру l , и преобразованием полученого графа в простой граф – объединение параллельных ребер (рис. 3.39).
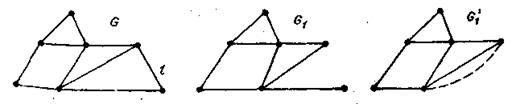
Рис. 3.39
С помощью лемм 1 – 4 можно свести задачу подсчета числа правильных раскрасок к более простым задачам, через расширение которых можно найти окончательный результат.
Интересным классом графов с точки зрения подсчета числа правильных раскрасок являются однозначно раскрашиваемые графы. Граф G называется однозначно 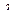 -раскрашенным (h=(G) =
-раскрашенным (h=(G) = 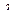 ), если каждая
), если каждая 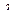 -раскраска порождает одно и то же разбиение вершин. Граф G, представленный на рис. 3.40, а, однозначно 3-раскрашиваем, так как каждая его 3-раскраска дает разбиение
-раскраска порождает одно и то же разбиение вершин. Граф G, представленный на рис. 3.40, а, однозначно 3-раскрашиваем, так как каждая его 3-раскраска дает разбиение 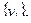
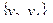
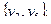 Граф G2 (рис.3.40,б) не однозначно 3-раскрашиваем: возможны, пять различных разбиений множества его вершин. В любой
Граф G2 (рис.3.40,б) не однозначно 3-раскрашиваем: возможны, пять различных разбиений множества его вершин. В любой  - раскраске однозначно
- раскраске однозначно 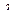 -раскрашиваемого графа каждая вершина v смежна, по крайней мере, с одной вершиной каждого цвета, отличного от цвета, приписанного v. Отсюда следует, что каждый однозначно
-раскрашиваемого графа каждая вершина v смежна, по крайней мере, с одной вершиной каждого цвета, отличного от цвета, приписанного v. Отсюда следует, что каждый однозначно 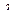 -раскрашиваемый граф (
-раскрашиваемый граф ( 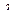 -1) связен и каждая его вершина имеет степень
-1) связен и каждая его вершина имеет степень  Для дальнейшего изучения структур, задеваемых с помощью графов, целесообразно рассмотреть матричное представление циклических свойств графов, которое тесно связано с вопросами нахождения разрезов (для плоских графов задача перечисления разрезов, эквивалентна задаче перечисления циклов двойственного графа). Введем для исследования циклов в графе циклометрическую матрицу (матрицу цикла). Каждому циклу графа взаимно однозначно сопоставляется вектор-строка матрицы С(G). Каждый элемент этой строки определяется следующим образом:
Для дальнейшего изучения структур, задеваемых с помощью графов, целесообразно рассмотреть матричное представление циклических свойств графов, которое тесно связано с вопросами нахождения разрезов (для плоских графов задача перечисления разрезов, эквивалентна задаче перечисления циклов двойственного графа). Введем для исследования циклов в графе циклометрическую матрицу (матрицу цикла). Каждому циклу графа взаимно однозначно сопоставляется вектор-строка матрицы С(G). Каждый элемент этой строки определяется следующим образом:
 1, если j ребро входит в i-й цикл;
1, если j ребро входит в i-й цикл;
Cij =
0 в противном случае.
Множество C (G) всех векторов, каждый из которых соответствует одному циклу графа G, образует векторное пространство (пространство циклов графа). При этом выполняются следующие условия:
– для любых двух циклов 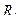
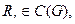
 существует некоторый третий цикл
существует некоторый третий цикл 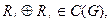 где
где 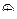 означает подразрядное сложение по модулю два;
означает подразрядное сложение по модулю два;
– сложение по модулю два обладает свойством коммутативности, т.е. для любых 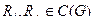
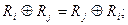
– сложение по модулю два ассоциативно, т.е. для любых 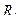
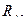
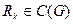
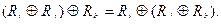


Рис. 3.40 Рис. 3.41
Базисом векторного пространства называется всякая система линейно независимых векторов, порождающая данное пространство. Множество векторов тогда и только тогда является базисом векторного пространства, когда всякий элемент этого пространства единственным образом представим в виде линейной комбинации векторов множества. Любой вектор цикла графа G может быть представлен в виде линейной комбинации векторов базиса циклов. Например, для графа, изображенного на рис.3.41, в качестве базисных циклов можно взять циклы R1, R2, R3. Цикломагическая матрица данного графа имеет вид
 | |||
 | |||

| b | c | d | e | f | m | g | h |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
С(G) =
Если связный граф G имеет n вершин и m ребер, то число базисных циклов в графе равно его цикломатическому числу 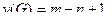 Если граф G содержит k компонент связности, то его цикломатическое число
Если граф G содержит k компонент связности, то его цикломатическое число
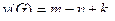
Выполняя 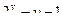 раз операцию сложения по модулю два над базисными циклами, получаем все множество циклов этого пространства. Задавая в графе свойства циклов, можно определить тот или иной класс графов. Например, для двудольного графа все циклы будут четной длины (четны). Аналогично матрице циклов можно составить матрицу разрезов, описывавшую все простые разрезы графа. Например, для графа, изображенного на рис.3.42, простыми разрезами будут
раз операцию сложения по модулю два над базисными циклами, получаем все множество циклов этого пространства. Задавая в графе свойства циклов, можно определить тот или иной класс графов. Например, для двудольного графа все циклы будут четной длины (четны). Аналогично матрице циклов можно составить матрицу разрезов, описывавшую все простые разрезы графа. Например, для графа, изображенного на рис.3.42, простыми разрезами будут 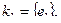

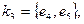
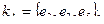
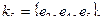
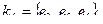
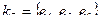 При этом матрица разрезов имеет вид
При этом матрица разрезов имеет вид
 |  |
| е1 | е2 | е3 | е4 | е5 | е6 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 |
K1
К2
К3
К = К4
К5
К6
К7

Рис. 3.42
Между матрицей циклов С и матрицей разрезов К любого графа существует соотношение СК'= 0. Аналогичное соотношение имеется между матрицей инциденций и матрицей циклов: SC′ = 0.
Для ориентированных и неориентированных графов определяются еще матрицы смежности вершин, смежности ребер, матрицы путей для различных пар вершин (более общим является матрица достижимости, рассмотренная ранее) [13].
Операции над графами
Для представления графов в виде композиции более простых графов введем следующие три операции: объединение, сумму и произведение.
Объединением графов 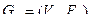 и
и 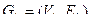 называется граф
называется граф 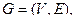 носитель и сигнатура которого являются соответственно теоретико-множественным объединением носителей
носитель и сигнатура которого являются соответственно теоретико-множественным объединением носителей 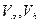 и сигнатур
и сигнатур 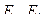 графов
графов 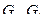 (рис.3.43,а).
(рис.3.43,а).
Суммой графов 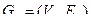 и
и 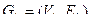 называется граф
называется граф 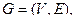 представляющий собой объединение графов
представляющий собой объединение графов 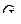 и
и 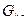 каждая вершина
каждая вершина  , не вошедшая в пересечение
, не вошедшая в пересечение 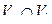 , соединяется со всеми вершинами
, соединяется со всеми вершинами 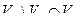 и наоборот (рис.3.43,б).
и наоборот (рис.3.43,б).
Декартовым произведением графов 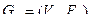 и
и 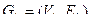 называется граф
называется граф 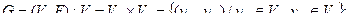
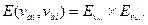
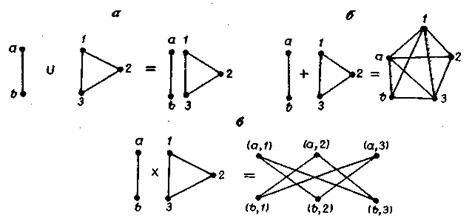
Рис. 3.43
Для этих основных операций определим хроматическое число полученных графов через хроматические числа исходных графов.
Хроматическое число h (G) графа G:
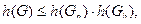 где
где 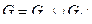
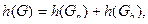 где
где 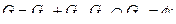
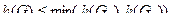 где
где 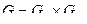 (3.19)
(3.19)
При решении оптимизационных задач дискретной математики вводят понятие производной, основанное на использовании понятия частоты букв и словах некоторой модели  Для корректного введения этого понятия рассмотрим предварительно вопросы, связанные с введением возможности придать некоторые свойства вершинам, существенно отличным от простой принадлежности некоторому множеству. Такими свойствами" на первом этапе могут быть некоторые функции от входящих дуг, например логические функции.
Для корректного введения этого понятия рассмотрим предварительно вопросы, связанные с введением возможности придать некоторые свойства вершинам, существенно отличным от простой принадлежности некоторому множеству. Такими свойствами" на первом этапе могут быть некоторые функции от входящих дуг, например логические функции.
Дата добавления: 2018-11-24; просмотров: 471; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
