Варианты построения оснований математической общей теории систем
В основу математической общей теории систем могут быть положены те или иные системные концепции математики. Наиболее общие из них опираются на теорию множеств и теорию отношений. Имеющиеся до настоящего времени варианты построения математической общей теории систем непосредственно или косвенно опираются на теорию множеств и отношений. В настоящее время различают теоретико-множественный, структурно-математический, логико-алгебраический и категорийно-функторный варианты построения оснований математической общей теории систем.
Перечисленные варианты в основном исходят из сложившихся наиболее общих конструкций математики. Задача математической общей теории систем состоит в трансформации соответствующих фундаментальных положений математики, связанных с данными конструкциями, в общие задачи исследования абстрактных и материальных систем. При нашем изложении будем придерживаться в основном теоретико-множественного подхода [7-9].
Множества. Основные определения.
Операции над множествами
Под множеством понимают объединение в одно общее объектов, хорошо различаемых нашей интуицией или нашей мыслью. Это определение принадлежит основателю теории множеств Георгу Кантору. Существует ряд других определений понятия множества, так или иначе апеллирующих к интуитивному смыслу этого понятия. Поэтому понятие множества в математике является первичным и, следовательно, не имеет строгого определения, удовлетворяющего современным требованиям.
|
|
|
Объекты, которые образуют множество, будем называть элементами множества и обозначать, как правило, малыми буквами латинского алфавита, сами множества – большими латинскими буквами А, В, С, О, X, У и т.д. Принадлежность элемента х к множеству X фиксируется записью  . Противоположное утверждение записывается в виде
. Противоположное утверждение записывается в виде 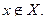 Множество У называется подмножеством (частью множества) X, если оно содержит только элементы, входящие в X. Формальная запись при атом имеет вид
Множество У называется подмножеством (частью множества) X, если оно содержит только элементы, входящие в X. Формальная запись при атом имеет вид 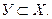 Два множества X и У равны тогда, когда имеет место
Два множества X и У равны тогда, когда имеет место  и
и  т.е. множества состоят из одинаковых элементов (при этом наличие повторяющихся элементов не принимается во внимание). Если
т.е. множества состоят из одинаковых элементов (при этом наличие повторяющихся элементов не принимается во внимание). Если  и
и 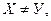 множество У называется собственным подмножеством X.
множество У называется собственным подмножеством X.
Различают конечные множества, состоящие из конечного числа элементов, и бесконечные множества, число элементов которых бесконечно. Если множество не содержит ни одного элемента, то оно называется пустым и обозначается 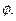
Множество может быть задано различными способами: конечное множество  может быть задано простым перечислением его элементов, записываемых в фигурных скобках:
может быть задано простым перечислением его элементов, записываемых в фигурных скобках: 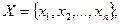 другой способ, используемый при задании как конечных, так и бесконечных множеств, состоит в указании свойства Р(х), которым обладают элементы данного множества
другой способ, используемый при задании как конечных, так и бесконечных множеств, состоит в указании свойства Р(х), которым обладают элементы данного множества 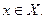
|
|
|
В качестве такого свойства, например, может рассматриваться принадлежность элемента х к одному из следующих видов отрезков вещественной оси: замкнутому 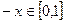 , разомкнутому
, разомкнутому 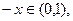 замкнутому слева
замкнутому слева 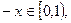 замкнутому справа
замкнутому справа 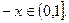 .
.
Для каждого множества 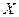 существует множество, элементами которого являются подмножества множества
существует множество, элементами которого являются подмножества множества 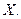 Такое множество называется булеаном множества и обозначается В (х). Так, булеаном множества
Такое множество называется булеаном множества и обозначается В (х). Так, булеаном множества 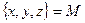 будет
будет
B(M) = 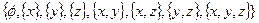 (2.1)
(2.1)
Очевидно, что мощность (число элементов для конечных множеств)  булеана равна
булеана равна  Одним из понятий теории множеств является понятие декартова (прямого) произведения множеств, которое является одной из основных математических конструкций.
Одним из понятий теории множеств является понятие декартова (прямого) произведения множеств, которое является одной из основных математических конструкций.
Декартовым произведением n множеств 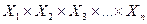 называется множество упорядоченных n-ок (упорядоченных наборов длины n, кортежей длины n), таких, что первый элемент принадлежит
называется множество упорядоченных n-ок (упорядоченных наборов длины n, кортежей длины n), таких, что первый элемент принадлежит  второй –
второй – 
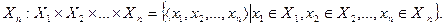 В частности, если имеет место
В частности, если имеет место 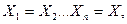 декартово произведение называется n-кратным или декартовой n-й степенью и обозначается
декартово произведение называется n-кратным или декартовой n-й степенью и обозначается  . Для декартовых произведений может использоваться геометрическая интерпретация. В атом случае множества
. Для декартовых произведений может использоваться геометрическая интерпретация. В атом случае множества  называются осями координат n-мерного пространства, а кортежи <х1, х2,..., хn > – точками этого пространства. Случай n = 2 декартова произведения множеств А и В приведен на рис. 2.1.
называются осями координат n-мерного пространства, а кортежи <х1, х2,..., хn > – точками этого пространства. Случай n = 2 декартова произведения множеств А и В приведен на рис. 2.1.
|
|
|
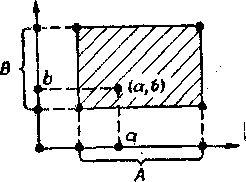
Рис. 2.1
Дальнейшее обобщение понятия, декартова произведения возможно путем введения булеанов как от исходных множеств, так и от формируемых декартовых произведений. Н.Бурбаки назвал конструируемое таким обрамим множество 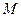 ступенью шкалы, строящийся над базисными множествами
ступенью шкалы, строящийся над базисными множествами 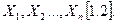 Определение множества
Определение множества  производится за
производится за  шагов путем последовательного построения множеств
шагов путем последовательного построения множеств  в соответствии с заданной схемой образования (схемой конструкции) ступени
в соответствии с заданной схемой образования (схемой конструкции) ступени 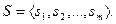 Элемент
Элемент 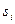 последнего кортежа представляют собой пары
последнего кортежа представляют собой пары  определяющие
определяющие 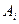 по следующему правилу:
по следующему правилу:
а) если  и
и 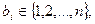 принимается
принимается 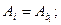
б) если 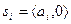 и
и 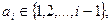 принимается
принимается 
в) если 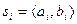 и
и 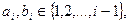 принимается
принимается 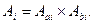
Очевидно, что на этом пути могут быть получены образования, включающие в качестве частных случаев различные декартовые произведения базисных множеств 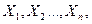 булеаны этих множеств и их декартовых произведений, декартовы произведения базисных множеств и их булеанов и т.д. вплоть до формирования на последнем m-м шаге множества
булеаны этих множеств и их декартовых произведений, декартовы произведения базисных множеств и их булеанов и т.д. вплоть до формирования на последнем m-м шаге множества 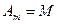 как угодно сложной конструкции. Это множество и есть ступень над базисными множествами
как угодно сложной конструкции. Это множество и есть ступень над базисными множествами 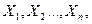 построенная по схеме
построенная по схеме  и обозначаемая
и обозначаемая
|
|
|
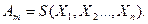 Например, пусть
Например, пусть  – базисные множества. Если
– базисные множества. Если 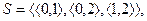 имеем
имеем 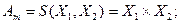 если
если 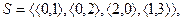 имеем
имеем  если
если 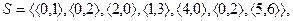 то
то 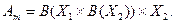
Множества X к У называются эквивалентными, или множествами одинаковой мощности 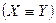 , если между их элементами существует взаимно однозначное соответствие, т.е. каждому элементу
, если между их элементами существует взаимно однозначное соответствие, т.е. каждому элементу  соответствует один и только один элемент
соответствует один и только один элемент 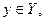 и наоборот. Данное определение является основой для анализа важнейшей характеристики множеств – их мощности. Конечное множество
и наоборот. Данное определение является основой для анализа важнейшей характеристики множеств – их мощности. Конечное множество 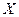 можно поставить во взаимно однозначное соответствие с частью натурального ряда чисел
можно поставить во взаимно однозначное соответствие с частью натурального ряда чисел  путем перенумеровки членов данного множества.
путем перенумеровки членов данного множества.
Мощность множеств характеризуется так называемыми кардинальными числами. Кардинальное число конечного множества  , состоящего из
, состоящего из 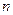 элементов, равно
элементов, равно  (card
(card  ). Кардинальное число булеана данного множества определяется следующим образом: card
). Кардинальное число булеана данного множества определяется следующим образом: card 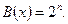 Бёсконечным множествам соответствуют бесконечные числа. Бесконечные множества делятся на счетные (бесконечностные) и несчетные. Счетные множества – это такие множества, которые могут быть поставлены во взаимно однозначное соответствие с натуральным рядом чисел
Бёсконечным множествам соответствуют бесконечные числа. Бесконечные множества делятся на счетные (бесконечностные) и несчетные. Счетные множества – это такие множества, которые могут быть поставлены во взаимно однозначное соответствие с натуральным рядом чисел 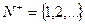 и имеют, следовательно, мощность данного ряда. Последняя выражается бесконечным кардинальным числом
и имеют, следовательно, мощность данного ряда. Последняя выражается бесконечным кардинальным числом 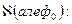
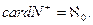 Алеф0 является наименьшим числом в ряду бесконечных чисел, оценивающих мощность бесконечных множеств, так называемы: трансфинитов. В качестве следующего числа обычно рассматривается
Алеф0 является наименьшим числом в ряду бесконечных чисел, оценивающих мощность бесконечных множеств, так называемы: трансфинитов. В качестве следующего числа обычно рассматривается 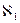 (алеф1), равный кардинальному числу булеана натурального ряда чисел
(алеф1), равный кардинальному числу булеана натурального ряда чисел 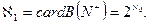 Такую мощность имеет множество вещественных чисел, находящихся в пределах отрезка [0,1]. Множества, кардинальные числа которых равны
Такую мощность имеет множество вещественных чисел, находящихся в пределах отрезка [0,1]. Множества, кардинальные числа которых равны 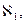 , называются континуальными, или множества мощности континуума. Следующими рассматриваются множества с кардинальными числами
, называются континуальными, или множества мощности континуума. Следующими рассматриваются множества с кардинальными числами 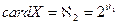 и т.д. [1. 7].
и т.д. [1. 7].
Например, кардинальное число множества всех вещественных функций равно 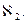 Предположения о том, что кардинальное число
Предположения о том, что кардинальное число 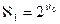 непосредственно следует за
непосредственно следует за 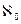 (континуум-гипотеза),
(континуум-гипотеза), 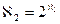 - за
- за 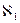 (обобщенная континуум-гипотеза), не могут быть не доказаны, ни опровергнуты, и поэтому эти предложения вводятся как аксиомы [1-7].
(обобщенная континуум-гипотеза), не могут быть не доказаны, ни опровергнуты, и поэтому эти предложения вводятся как аксиомы [1-7].
Для множеств вводятся операции объединения 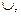 пересечения
пересечения 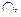 взятия разности \, определяемые указанием свойств
взятия разности \, определяемые указанием свойств 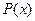 для элементов множества, получаемого в результате выполнения соответствующих булевских операций (см. рис. 2.2):
для элементов множества, получаемого в результате выполнения соответствующих булевских операций (см. рис. 2.2):
 или
или 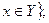
 или
или 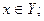 (2.2)
(2.2)
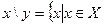 или
или 
х 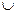 у х
у х  у
у
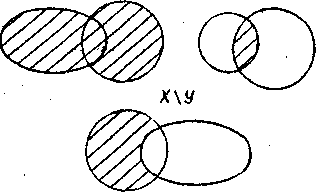
Рис. 2.2
Вводится также операция взятия симметрической разности 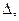 определяе-мая следующим образом:
определяе-мая следующим образом:
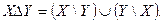 (2.3)
(2.3)
Путем непосредственного обобщения определяются операции объединения и пересечения семейства множеств 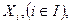 где
где 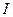 – множество индексов;
– множество индексов; 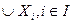 – это множество элементов, каждый из которых принадлежит хотя бы одному
– это множество элементов, каждый из которых принадлежит хотя бы одному 
 – это множество элементов, принадлежащих сразу всем
– это множество элементов, принадлежащих сразу всем 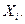 При этом выполняются следующие алгебраические законы:
При этом выполняются следующие алгебраические законы:
1)  (идемпотентность);
(идемпотентность);
2) 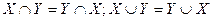 (коммутативность);
(коммутативность);
3) 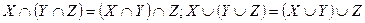 (ассоциативность);
(ассоциативность);
4) 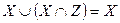 (поглощение);
(поглощение);
5) Если  то
то 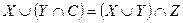 – модулярность;
– модулярность;
6) 
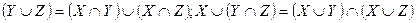 (дистрибутивность);
(дистрибутивность);
7) 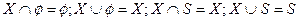 (универсальные границы);
(универсальные границы);
здесь S – универсум;
8) 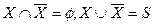 – дополняемость;
– дополняемость;
9)  (инволютивность);
(инволютивность);
10) 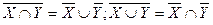 (законы де Моргана).
(законы де Моргана).
Другим важным понятием, которым мы будем часто пользоваться, является понятие разбиения. Разбиением данного множества X называется такое семейство множеств  где J – некоторое множество индексов и
где J – некоторое множество индексов и  при всех
при всех 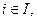 что
что
1) 
2) 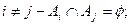
3) 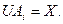
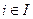
При заданном разбиении  мы пишем
мы пишем  когда х и у являються элементами одного и того же множества
когда х и у являються элементами одного и того же множества 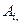 тем самым определено отношение, которое обозначается символом
тем самым определено отношение, которое обозначается символом 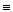 и обладает следующими свойствами:
и обладает следующими свойствами:
1) рефлексивностью: 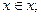
2) симметрией: 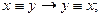
3) транзитивностью: 
Всякое отношение 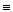 со свойствами 1, 2, 3 называется эквивалентностью. В свою очередь, эквивалентность
со свойствами 1, 2, 3 называется эквивалентностью. В свою очередь, эквивалентность 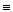 определяет, очевидно, разбиение множества X на множества вида
определяет, очевидно, разбиение множества X на множества вида  (где х0 – дання точка Х). Множество Аі называют классом эквивалентности, содержащим х0.
(где х0 – дання точка Х). Множество Аі называют классом эквивалентности, содержащим х0.
Пример 1. Пусть Р – целое число; пишем 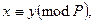 если х и у – два целых числа, отличающихся слагаемым, кратным Р. Ясно, что это отношение – эквивалентность.
если х и у – два целых числа, отличающихся слагаемым, кратным Р. Ясно, что это отношение – эквивалентность.
Пример 2. Если две прямые Д и Д/ параллельны или совпадают, то пишем Д ׀׀ Д/; очевидно, ׀׀ есть отношение эквивалентности.
Пример 3. Если у двух людей х и у глаза одинакового цвета, то пишем х 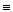 у, ясно, что
у, ясно, что 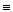 есть отношение эквивалентности.
есть отношение эквивалентности.
Пусть  и
и 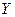 – два данных множества; закон
– два данных множества; закон 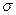 , согласно которому каждому элементу
, согласно которому каждому элементу  ставится в соответствие элемент
ставится в соответствие элемент 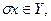 называется однозначным отображением Х в У, или функцией, определенной на X и принимающей значения в У; например, числовая функция вещественной переменной представляет собой однозначное отображение R в R (здесь R – множество вещественных чисел).
называется однозначным отображением Х в У, или функцией, определенной на X и принимающей значения в У; например, числовая функция вещественной переменной представляет собой однозначное отображение R в R (здесь R – множество вещественных чисел).
Многозначное отображение Г множества X в множество У есть закон, по которому каждому элементу  ставится в соответствие некоторое подмножество
ставится в соответствие некоторое подмножество 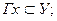 ; при этом не исключается возможность
; при этом не исключается возможность 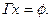
Говоря просто "отображение", большинство авторов подразумевают однозначное отображение. Поскольку нам предстоит иметь дело главным образом с неоднозначными отображениями, мы не придерживаемся упомянутого соглашения и понимаем слово отображение в широком смысле.
Пусть Г – отображение данного множества X в У. При 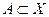 назовем образом множества А множество
назовем образом множества А множество 
Можно проверить, что если 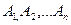 - подмножества Х, то
- подмножества Х, то
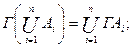
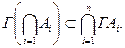 (2.4)
(2.4)
Если Г и ∆ – отображения множества X в Х , то результат композиции Г∆ есть отображение, определяемое следующим образом: (Г∆) х = Г(∆х).Отображения Г2, Г3,… – определяются так:
Г2х = Г (Гх);
Г3х = Г (Г2х);
…………….
Транзитивным замыканием отображения Г называется следующее отображение  множества Х в Х [1]:
множества Х в Х [1]:
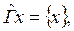
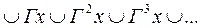 (2.5)
(2.5)
Отображение Г-1, обратное отображению Г, определяется так:

Если В  , то полагаем
, то полагаем 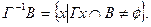
Пример 1. Возьмем в качестве  множество людей и для
множество людей и для 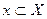 обозначим через Гх множество детей человека х. Тогда: Г2 – множество внуков х;
обозначим через Гх множество детей человека х. Тогда: Г2 – множество внуков х;  х – множество, состоящее из х и всех его потомков; Г-1 – родители и т.д.
х – множество, состоящее из х и всех его потомков; Г-1 – родители и т.д.
Изображая людей точками и рисуя стрелку, идущую из х в у, в случае, когда х является отцом или матерью у, мы получим родословное или генеалогическое дерево.
Пример 2. Рассмотрим шахматную игру; каждое положение задается диаграммой (местонахождением фигур в данный момент) и ходом (указанием, кто из игроков должен в этот момент играть).
Пусть  – множество возможных положений, Гх (где
– множество возможных положений, Гх (где  ) – множество положений, которые по правилам игры можно получить непосредственно из х; если положение х – матовое или патовое, то Гх =
) – множество положений, которые по правилам игры можно получить непосредственно из х; если положение х – матовое или патовое, то Гх =  . Имеем: Г3х – множество положений, которые можно получить из х тремя ходами; Г – множество положений, которые вообще можно рано или поздно получить, отправляясь от х; Г'-1А (где А
. Имеем: Г3х – множество положений, которые можно получить из х тремя ходами; Г – множество положений, которые вообще можно рано или поздно получить, отправляясь от х; Г'-1А (где А 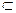 X – множество тех положений, из которых возможно одним ходом получить какое-либо положение, входящее в А). Такая система обозначений позволяет выразить формулой множество выигрышных положений и вывести отсюда ряд свойств. В случае шахмат правила игры полностью определяются множеством X и отображением Г; однако здесь мы имеем дело с таким большим числом положений, что изобразить все их точками, а отношение Г – стрелками, соединяющими некоторые точки, практически невозможно. Тем не менее некоторые свойства, общие для правил шахматной игры и для отношений родства в группе людей, можно выявить, обращаясь к аксиоматическому методу.
X – множество тех положений, из которых возможно одним ходом получить какое-либо положение, входящее в А). Такая система обозначений позволяет выразить формулой множество выигрышных положений и вывести отсюда ряд свойств. В случае шахмат правила игры полностью определяются множеством X и отображением Г; однако здесь мы имеем дело с таким большим числом положений, что изобразить все их точками, а отношение Г – стрелками, соединяющими некоторые точки, практически невозможно. Тем не менее некоторые свойства, общие для правил шахматной игры и для отношений родства в группе людей, можно выявить, обращаясь к аксиоматическому методу.
ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ
Теория графов дает простой, доступный и мощный инструмент построения моделей и решения задач упорядочения объектов. В настоящее время существует множество проблем, где требуется построить сложные системы с помощью упорядочения их элементов. Сюда относятся календарное планирование промышленного производства, задачи теории сетевого планирования и управления, тактические и логические задачи, проблемы построения систем связи и исследования процессов передачи информации, выбор оптимальных маршрутов и потоков в сетях, методы 'построения электрических сетей, задачи идентификации в органической химии и способы построения переключательных схем. Комбинаторные методы нахождения нужного упорядочения объектов существенно отличаются от классических методов анализа поведения систем с помощью уравнений. Кроме языка теории графов задачи упорядочения объектов можно формулировать в терминах теории матриц с элементами ноль-один или в терминах теории конечных множеств. Однако с полным основанием можно сказать, что теория графов является одним из простейших и наиболее элегантных разделов современной математики с широкой областью применения. Имея в своей основе простейшие идеи и элементы – точки, соединенные линиями, теория графов строит из них богатое многообразие форм, наделяя эти формы интересными свойствами, и в результате становится полезным инструментом при исследовании самых разнообразных систем [10].
Вместо понятия графа часто используется понятие "сеть",Это особенно относится к случаям, когда кроме основных чисто структурных соотношений в графе задаются некоторые количественные характеристики точек и линий, образующих граф. В качестве примера можно назвать электрические сети, сети выполнения работ в проектах, сети потоков. При этом ребрам сети ставятся в соответствие определенные количественные характеристики энергии, затрат и потока [11].
Дата добавления: 2018-11-24; просмотров: 265; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
