Логический вывод решений с помощью исчисления предикатов

 

Для получения новых знаний и решений необходимы знания, представленные в виде предикатов в той или иной форме, преобразовать, т.е. доказать некоторые соотношения. Доказательство демонстрирует, что некоторая правильно построенная формула является теоремой на задан­ном множестве аксиом, т.е. результатом, логически выводимым из ак­сиом. Однако алгоритмы, принятые в реальной действительности, опи­сывают доказательство в несколько измененном виде [17, 20].

Положим, что есть множество, состоящее из  и пусть формула, для которой требуется выяснить, является ли она тео­ремой, есть В. В таком случае доказательство показывает справедли­вость

                                               (4.38)

при любой ее интерпретации. Можно сказать и по-иному: такое опреде­ление эквивалентно тому, что отрицание формулы (4.38), т.е.

                                                 (4.39)

не выполняется (является ложью) при любой интерпретации. Поскольку формула (4.39) является правильно построенной формулой, то ее можно преобразовать в форму клаузального множества, используя для этого описанный выше алгоритм. Пусть это преобразование есть S. Метод резолюции является одним из методов доказательства возможности преобразования, однако его основная идея состоит в проверке того:

- содержит или не содержит S пустое предложение;

- выводится или не выводится пустое предложение из S, если
пустое предложение в S отсутствует.

Любое предложение C₁ из которого образуется S, является сово­купностью атомарных предикатов или их отрицаний (предикат и его от­рицание вместе называются литералом), соединенных символом дизъюнкции, вида:

                                                     (4.40)

Само же S является конъюнктивной формой, т.е. имеет вид:

                                               (4.41)

Следовательно, условием истинностиSи является условие истинности всех  С_і в совокупности, и наоборот, условием ложности S является ложность, по крайней мере, одного C_i. Однако, C_i имеет вид (4.40), и поэтому условием того, что С_i в какой-нибудь интерпретации будет ложным, является то, что множество {P_i1,….P_im} будет пустым. Это видно из следующего. Положим, что это не так, тогда среди всех всевозможных интерпретаций имеется такая, что какой-нибудь из литералов P_i1, ... Р_im или все они будут истиной, и поэтому С_i в общем случае не будет ложью. Следовательно, если S содержит пустое предложение, формула (4.39) является ложью, поэтому является ложью и предыдущая формула (4.38), а это показывает, что B выводится из группы предикатов А₁, А₂,…, А_n т.е. из Σ. Второй шаг (2) -про­верка наличия пустого предложения в S означает проверку этого ре­зультата после того, как будут выполнены преобразования с помощью правил вывода в S .

Рассмотрим вначале применение метода резолюций для высказыва­ний, так как предикат , который не содержит переменных, совпадает с высказыванием. Положим, что во множестве предложений имеются допол­нительные литералы (литералы, которые взаимно отличаются только сим­волом отрицаний - в данном случае   z и 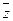) вида:

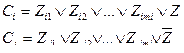                                      (4.42)

Исключим из этих двух предложений дополнительные литералы и пред­ставим оставшуюся часть в дизъюнктивной форме (такое представление называется резольвентой С_i и C_j ) ;

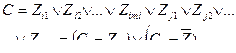                           (4.43)

После проведения этой операции можно увидеть, что С является логическим заключением из Ci и Сj. Следовательно, добавление С к множеству S не влияет на вывод об истинности или ложности S . Если выполняется Cj=z, Cj= 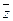 то С пусто. Тот факт, что С является логическим заключением из S и С - пусто, указывает на ложность исходной логической формулы. Рассмотрим пример:

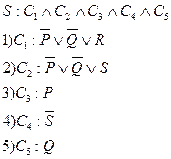
Получение следующего доказательства принципом резолюции:

6) резольвента (2) и (3);

7) 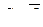резольвента (4) и (6);

8) 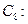 □ резольвента (5) и (7);

□ - пустое предложение.

Поскольку в логике предикатов внутри предикатов содержатся пе­ременные, то алгоритм доказательства несколько усложняется. В этом случае перед тем, как применять описанный алгоритм, будет предва­рительно проведена некоторая подстановка в переменные и введено по­нятие унификации с помощью этой подстановки. Унификацию проиллюст­рируем простым примером. Рассмотрим два предиката Z(x) и Z(α). Положим, что х – переменная, а – константа. В этих предикатах предикатные символы одинаковы, чего нельзя сказать о самих преди­катах. Тем не менее подстановкой α в x эти предикаты можно сде­лать одинаковыми (эта подстановка называется унификацией). Целью унификации является обеспечение возможности применения описанного выше алгоритма доказательства для предикатов. Обобщив пример фор­мулы (4.42) для предикатов, получим:

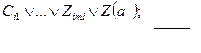
В данном случае  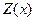и 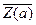 не находятся в дополнительных от­ношениях. При подстановке  вместо 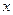 будет получено соответствен­но  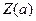и 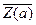, и эти предикаты находятся в дополнительных отно­шениях. Однако операция подстановки имеет ограничения.

Подстановку t в x будем обозначать {t/x}. Поскольку в од­ну формулу может входить более одной переменной и можно произвес­ти более одной подстановки, то эти подстановки записываются в виде множества упорядоченных пар:

{t₁/x_1,t₂/x₂,…,t_n/x_n}                                           (4.45)

Условия, допускающие подстановку:

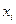-  является переменной, a t₁-термом (константа, пере-­
менная, символ функции), отличным от x ;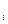

- для любой пары элементов из группы подстановок, например
 и  в правых частях символов "//", не содержится оди-­
наковыx переменных.

Обозначим группу подстановок { 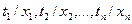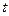} через Ө. Когда для некоторого представления Z применяется подстановка содержащихся в ней переменных { }, то результат под­становки, при котором переменные заменяются соответствующими им пе­ременными t₁,t₂...t_n принято обозначать ΖӨ. Если имеется груп­па различных выражений предиката Ζ, т.е. {Ζ₁, Ζ₂,…,Ζ_m}, то под­становка Ө (положим, что она существует) такая, что в результате все эти выражения становятся одинаковыми, т.е. Ζ₁Ө=Ζ₂Ө=…=Ζ_mӨ называется унификатором для {Ζ_1,Z₂…Z_m}. Если подобная подстановка Ө существует, то говорят, что множество выражений {Z₁, Z₂ ...,Zm} унифицируемо. В предыдущем примере множество {Z(х), Z(а)} уни­фицируемо, при этом унификатором является подстановка {a/x} .

Для одной группы выражений унификатор не обязательно единст­венный. Для группы выражений{Z(х,у), Z(z, f(x))} подстановка Ө={x/z, f(x)/y} является унификатором, но является также унифика­тором и подстановка Ө={a/x, a/z, f(a)/y}. Здесь, как и ранее,  является константой, а х - переменной. В таких случаях возникает естественная проблема, какую подстановку лучше всего выбрать в ка­честве унификатора.

Операцию подстановки можно провести не за один paз, а разде­лить ее на несколько этапов. Ее можно также разделить по группам пе­ременных, проведя, например, подстановку в виде:

{ }

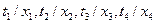сначала для { 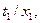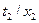}, затем для { 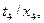}. Допустимо также подстановку вида a / x разбить на две подстановки u / x и а/ u (принимается, что x и u переменные). Результат последовательного выполнения двух подстановок Ө и λ также является подстановкой. Та­кая подстановка является сложной и обозначается в виде .

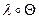Если существует несколько унификаторов, то среди них найдется такая подстановка σ, что все другие унификаторы являются подстанов­ками, выражаемыми в виде σ о λ, как сложная форма, включающая эту подстановку. В результате подстановки переменные будут замещены кон­стантами и описательная мощность формулы будет ограничена. Чтобы унифицировать два различных выражения предиката, необходима такая подстановка, при которой выражение с большей описательной мощностью согласуется с выражением, имеющим малую описательную мощность. Одна­ко совсем нет необходимости ограничивать описательную мощность все­ми другими подстановками. Подстановка является унификатором с самы­ми минимальными ограничениями подобного вида. В этом смысле ее при­нято называть "наиболее общим унификатором" (НОУ).

Алгоритм нахождения НОУ сравнительно прост. Он состоит в том, что сначала упорядочиваются выражения, которые подлежат унификации, (каждое выражение будет упорядочено в алфавитном или символьном по­рядке), среди них отыскивается такое, в котором соответствующие тер­мы не совпадают между собой. Пусть при осмотре последовательно всех выражений в порядке слева направо несовпадающими термами явились x , t . Например, получено выражение {Ζ (a , t , f ( z )), Z( a , x , z )}. В этом слу­чае, если:

1) х является переменной;

2) x не содержится в t,

к группе подстановок добавляется {t / x}.

Если повторением этих операций будет обозначено совпадение всех изначально заданных выражений, то они являются унифицируемыми, а груп­па полученных подстановок является НОУ.

В приведенном примере третий терм есть в одном случае z, а в другом f ( z ), условие I выполняется, однако условие II нарушается и поэтому подстановка является недопустимой. Если же в группе преди­катных выражений остается хотя бы одно такое, для которого никакими подстановками нельзя получить совпадение с другими выражениями, та­кая группа выражений является неунифицируемой. Рассмотрим пример на нахождение НОУ:

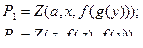                                                          (4.46)

I. Самые первые несовпадающие члены при рассмотрении слева направо: {a , z }→ подстановка a / z . Из этого получается

 

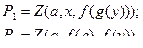
2. Самые первые несовпадающие члены при рассмотрении слева направо: {x , f ( a )} →подстановка { f ( a )/ x}.

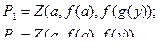
Подстановка: {а/ z , f ( a )/ x}.

3. Добавляется {g ( y )/ v}. Теперь оба выражения совпадают, поэтому унификация заканчивается НОУ: {a / z , f ( a )/ x , g ( y )/ v}.

Рассмотрим алгоритм доказательства методом резолюции в логике предикатов. Различие по сравнению исчисления высказываний в том, что здесь создаются дополнительные литералы с помощью операции под­становки. Применение метода резолюции рассмотрим для доказательства секвенций.

Допустим, что знания представлены логическими формулами A ₁ ,…, A_{m ,} a последовательность этих формул обозначена буквой Г. Что­бы проверить, можно ли на основе этих знаний вывести новый факт В, представленный формулой, следует проверить возможность существова­ния доказательства Г→В. Если доказательство существует, то гово­рят «выражение Г→В доказуемо» и записывают ├Г→В. В данном случае говорят также, что В доказуемо на основании Г и записывают Г├ В. Если Г - пустая последовательность (m = 0), то записывают ├В и говорят, что В доказуемо. Запись ├ Г→ означает, что Г - противоречивая последовательность, во всех других случаях говорят, что Г - непротиворечивая последовательность. Следовательно, если Г - противоречивая последовательность, то с помощью правила выводя →Т для любого С можно получить Г├ С. И наоборот, если все фор­мулы доказуемы на основании Г, то можно записать Г├С, кроме того, поскольку Г ├ С, получаем доказательство Г→. Следовательно, дока­зуемость всех формул на основании Г можно трактовать как определе­ние противоречивости. Другими словами, из противоречивых знаний можно вывести любой факт.

Рассмотрим теперь интерпретацию секвенции, которую будем рассматривать как формулу. Допустим, что существует некоторая секвен­ция S, и попытаемся определить ее интерпретацию J. Обозначим константы входящие в S, через C₁ C₂,.., С_k , функциональные символы – через f_1,f ₂ ,…, f_m, а предикатные символы - через P₁,P₂,…,P_n.Для однозначного определения необходимо рассмотреть множество всех индивидумов, которые являются структурными элементами описы­ваемой в данный момент предметной области. Это множество назовем универсумом U. U может быть любым не пустым множеством (например, множество технологических операций).Для определения J необходимо определить, какой элемент идентифицирует каждая константа C_i (1≤ i ≤ k ). Функциональный символ     f_i (1≤ i ≤ m ) интерпретируется как функ­ция в предметной области. Например, f_i• - функциональный j-мест­ный символ. Тогда, если заданы j элементов a ₁ ,а₂,..,, а _j множества U, то ее значение интерпретируется как функция, принимающая некоторое значение b в множестве U. Таких функций обычно много, но для определения J необходимо знать, какой функции соответствует каждое f_i. И наконец, предикатный символ P_i (1≤ i ≤ n ) интерпрети­руется как отношение в предметной области U. Допустим теперь, что P_j- j-местный предикатный символ, тогда при установлении отноше­ния R ( a ₁ , a ₂ ,..., a_j ) между j элементами а₁, а₂,..., а _j; множества U или неустановлении его, он интерпретируется как такое отноше­ние. При этом, когда отношение установлено, предикатный символ на­зывается истиной, в противном случае - ложью. Так как подобных от­ношений также множество, то для определения J устанавливается со­ответствие отношений для каждого P_i. Благодаря этому можно найти однозначную интерпретацию J секвенции S. Если интерпретация J оп­ределена, то очевидно, что все термы, не имеющие переменных в сек­венции S, можно интерпретировать как элементы множества U. Анало­гично атомарные (элементарные) высказывания, не имеющие переменных, определяются истиной или ложью в интерпретации J. Однако, при на­личии переменных (поскольку, когда переменная принимает значение эле­мента множества U, определяется истина или ложь) любое атомарное высказывание определяется истиной или ложью и происходит замена на интерпретацию логического символа. Интерпретация логического сим­вола не зависит от частной интерпретации J. Будем считать, что ис­тина или ложь относительно логической связки аналогичны алгебре высказываний. Тогда если в части ( х)(...x…) переменной x со­ответствует некоторый элемент множества U (предметной области) и если формулу в скобках можно интерпретировать как истину, то и эта часть интерпретируется как истина. В любом другом случаe она ин­терпретируется как ложь. Рассмотрим применение свободных перемен­ных. Обозначим свободные переменные секвенции S через x₁,..._,x_m, тогда если ( x₁)...( x_m)S в интерпретации J является истиной, то S называется достоверной в интерпретации J.

Если 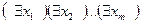 S - истина в интерпретации J, то S называется выполнимой в интерпретации J. Разумеется, если S дос­товерна в интерпретации J, то она выполнима в этой интерпретации. Кроме того, даже когда S - истинная секвенция, не содержащая сво­бодных переменных, то ее можно назвать достоверной. Если S досто­верна во всех интерпретациях, то она называется общезначимой. Если секвенция S доказуема, то она достоверна; верно и обратное: если секвенция S достоверна, то она доказуема. Этот факт означает, что для доказательства в системе выводов логики предикатов правильнос­ти всех секвенций не требуется других правил вывода (теорема Геделя о полноте).

Таким образом, если в логике предикатов существует последова­тельность формул Г, то дли любой формулы, не содержащей свободных переменных, казалось бы, должна быть справедлива одна из записей – Г├ A или Г├ 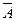. К сожалению, это не так. Eли Г содержит аксиомы математической логики и является непротиворечивой, то существует формула A ₁, не содержащая свободных переменных, такая, что оба при­веденных выше выражения не выводимы (теорема о неполноте Гегеля-Рос­са). Теорема о неполноте означает возможность ситуаций, когда нет смысла определять истину или ложь в программе вывода, составлен­ной на основании исчисления предикатов. Допустим, что в программе вывода доказывается формула A₁ , такая, Г├А и Г├  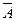не выпол­няются. В логике высказываний доказуемость или недоказуемость мож­но определить за конечное число шагов, но в логике предикатов та­кой метод не годится. Тем не менее это не является существенным не­достатком с точки зрении представления знаний и получения выводов. И основным методом получения выводов в программах, основанных на логике предикатов, является метод резолюции. Допустим, имеются фор­мулы А_1, A ₂ ,…, A_m. (отражающие, например, технологические операции) и формула В₁, для которых рассмотрим доказательство секвенций А₁,…, Am → B. Доказательство основано на достоверности, выражения  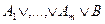которая вытекает из теоремы о полноте. Однако выполни­мость формулы Е не означает не выполнимость 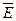. Другими словами, она эквивалентна невыполнимости. Это следует из определения достовер­ности и выполнимости и из выражений

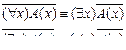
                                                 (4.47)

Где C ~ D означает, что С эквивалентно D. Поэтому можно считать, что ├С→ D и ├ D → C. Чтобы показать, что приведенные формулы являются достоверными, следует доказать с помощью, например, правил де Моргана невыполнимость формулы . Для этого данную формулу приведем к сколемовской конъюнктивной форме ( клаузальной форме). Пусть  обозначение литералов. Формула, в которой символом V объединены более одного литерала, как было ранее сказано, называется предложением (ctause),напри­мер 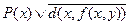. Далее, если C ₁ ,…, C_k – предложения, a x₁, x₂,…,x_m - различные переменные, содержащиеся в , то формула вида  называется клаузалъной формой. При это 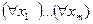называется префиксом, а логическое выражение в скобках - матрицей. И так, все формулы A можно преобразовать в клаузальные выражения A, причем если A выполни­мо, то выполнимо и A'. Следовательно, чтобы показать невыполни­мость A следует показать невыполнимость A '.

Запишем вначале алгоритм преобразования в клаузальную форму.                1. Преобразование A к виду

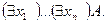
2. Переименуем переменные. Изменим связанные переменные при каждом символе  или  в формуле так, чтобы было соответствие различных переменных.

3. Удалим символы импликации →:

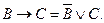
4.Переместим символ "-" внутрь 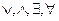 по формулам

 

5. Удалим . Крайний слева член в части формулы вида 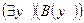 заменяется на  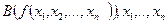- это свободные пе­ременные, появляющиеся в выражении  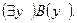Но для всей формулы это - переменные, ограниченные 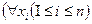в левой части ( 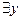)B(y). f - вновь выбранный функциональный n-местный символ, кото­рый до сих пор не употреблялся. Кроме того, при n = 0 он заменяет­ся на вновь выбранную константу, которая до сих пор не употребля­лась.  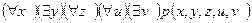принимает вид  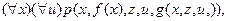  где p и g  - сколемовские функции. Аналогично  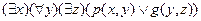принимает вид  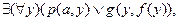где p,g - предикаты; а - сколемовская константа, f - сколемовская функция.

6.Переместим  вперед (часть 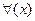 перемещается в префиксную часть формулы) .

7. Переместим символ  относительно символа 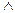. Следующая переста­новка повторяется по мере возможности:

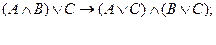                                 (4.48)

8. Минимизируем. Минимизация осуществляется с сохранением свойств выполнимости:

(1) удаляются литералы, неоднократно появляющиеся в предложе-
нии :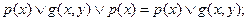

(2) удаляются предложения, литералы которых взаимно отрицают
друг друга:

Рассмотрим пример на применение п.1 - 7:

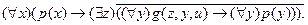
1.

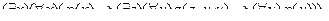
2.

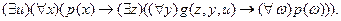
3.

4.                                                                          

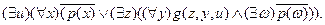
5. a - сколемовская константа ; f , q - сколемовские функции:

                          

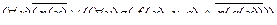
6.

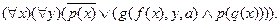
7.

Для того чтобы показать, что в клаузальной форме сохраняет­ся 'свойство выполнимости, следует показать, что при соответствую­щих преобразованиях согласно п.1 - 8 сохраняется свойство невыпол­нимости. Таким образом, принцип резолюции заключается в получении вывода по фразам матрицы клаузальной формы формулы с целью доказательство его невыполнимости.

Следующим разделом общего алгоритма является алгоритм унификации. Перед его применением дадим дополнительные сведения (по срав­нению с ранее рассмотренными вопросами унификации) и введем некоторые обозначения. Допустим, существуют две атомарные формулы, имеющие одинаковые предикатные символы, но не имеющие общих переменных, например 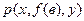 и 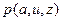. Если вместо х подставить а, вместо 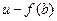, вместо y - z, то обе формулы станут оданадавыми. A именно 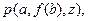т. е. они унифицируемы. Уточним запись под­становки с указанием стрелки { 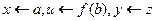} . Далее под­становки будем обозначать строчными буквами греческого алфавита  и т.д., а факт подстановки, например, в некоторое представление 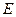 будем записывать как 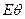  Если 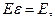 подстановка не содер­жит элементов. 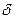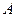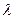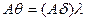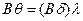Если существует некоторый унификатор  формул  и  , тогда если существует  такой, что для произвольного унификатора  справедливо  и , то 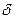 называется наиболее общим унификатором (НОУ). После унификации изменим последовательность литералов предложения и, собрав впереди отрицательные ли­тералы, получим следующую фразу:  данном случае это предложение представлено как секвенция 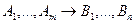. Различие между обычной секвенцией и предложение сос­тоит в том, что если в секвенци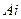и  и   являются обычными фор­мулами, то в предложении это - атомы (атомарные формулы). Предложение, в котором m = 0, n = 0, называется пустым. Так же как и в случае секвенции, атомарные формулы будем обозначать латинскими буквами 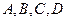 и т.д. или этими же буквами с индексами, а пропис­ными греческими буквами - конечный или пустой ряд атомов. Допустим, что в матрице клаузального выражения существуют два предложения:;

∆                                                     (4.49)

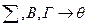                                                  (4.49а)

где А и В - атомарные формулы, имеющие одинаковые предикатные символы. Если при этом оба предложения имеют общие переменные, то, вы­полнив подстановку в одну из них, изменим ее так, чтобы они не име­ли общих переменных. Такая подстановка называется переименованием. Причина переименования заключается в следующем: пусть имеются два предложения С и D,Переименование в данном случае соответствует пре­образованию одной клаузальной формы, например , другую клаузальную форму, например 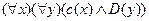.Введем те­перь переименовываемую подстановку  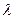и измени переменную в предложении . 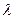Положим, что А и В  унифицируеми их НОУ есть 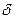. Правило вывода, с помощью которого из (4.49) и (4.49а) выводиться следующие предложение (4.50)называется резолюцией (разрешением):∆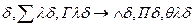

При этом само предложение (4.50), как уже было сказано, называется резольвентой. Если вместо переименования переменной в (4.49) выпол­нить переименование в (4.49а), резольвента будет иметь следующий вид:

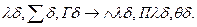
∆                                          (4.51)

где 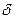 - НОУ атомов  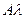и  .

Например, из предложения  и 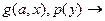 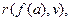с помощью резолюции получаем следующую резольвенту:

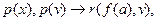
где переименовывающей подстановкой было { 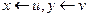} , а НОУ { }Если (4.49) и (4.49а) достоверны, то достовер­на и (4.51). Важным в резолюции является отсутствие общих перемен­ных в предпосылках. Поскольку резолюция предполагает исключение по одному соответствующему из двух предложений, являющихся предпосыл­ками, то назовем ее бинарной резолюцией. Однако одной лишь бинар­ной резолюции, как правила вывода недостаточно, необходимо еще од­но правило, называемое факторизацией. Допустим, что в предложениях

∆

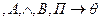
Г ∆ A , 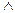B , П                                     (4.52)

атомы A и В унифицируемы и их НОУ есть 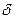. Тогда

∆

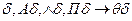
и                                                                                                               (4.53)

∆

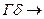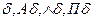
называются факторами предложений. Правило, с помощью которого из фразы С выводится фактор С, называется факторизацией. Например, фактор резольвенты 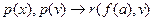 есть Допустим теперь, что задано множество предложений М, это множест­во является опровержимым, если существует ряд предложений 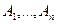 такой, что  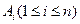является элементом М или фактором Ai (j < i) или резольвентой  и 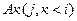, а А является пустым предложением→.При этом данный ряд называется опровержением множест­ва М. Рассмотрим пример. Множество М состоит из следующих предло­жений:

                                                     
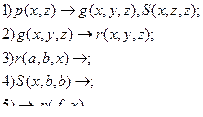
Опровержение М:

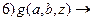 (резольвента 2 и З);

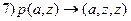(резольвента 1и 6);

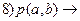(резольвента 4и7);

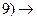(резольвента 5и8).

Итак, если на основании следующей теоремы секвенция является невыполнимой, это обстоятельство можно доказать в системе резолю­ций.

Теорема. Допустим, М - это множество предложений матри­цы в секвенции S клаузальной (или логической) формы, тогда невы­полнимость S эквивалентна опровержимости М. Другими словами, что­бы показать доказуемость некоторой секвенции в системе резолюций, отрицание этой секвенции преобразуется в клаузальную форму, и по его предложениям выполняются выводы.

Наиболее важной проблемой при программировании процесса опровержения является выбор двух предложений - посылок, при­годных для применения резолюции, или их факторов. Из­ложим основные принципы двух методов решения этой пробле­мы. Cтратегия приоритета простейшего предложения и множество поддержки. Стратегия приоритета простейшего предложения - это способ приоритетного выбора предложения, состоящего из одного литерала (простейшего предложения), в качестве посылки для резолюции. Он ос­нован на получении пустого предложения с помощью бинарной резолю­ции двух простейших предложений вида 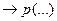 и 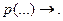 Концепция множества поддержки основана на идее максимального исключе­ния лишних выводов, поскольку среди элементов опровержимого мно­жества предложений М не исключена возможность существования пред­ложений, не имеющих отношения к опровержению, и вывод следует вы­полнять только на основе предложений, имеющих прямое отношение к опровержению. Для пояснения этого момента разделим множество пред­ложений M на два подмножества Т и М-Т ж рассмотрим их выполни­мость. Под выполнимостью множества предложений будем понимать выпол­нимость формулы, в которой все предложения, принадлежащие множеству, соединены связкой 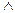, а все свободные переменные ограничению квантором . Допустим, что выполнимость М-Т очевидна, даже если неиз­вестна невыполнимость М. Тогда, выполняя вывод так, чтобы хотя бы одна из посылок, необходимых для применения резолюции, была предло­жением, принадлежащим подмножеству T, либо его фактором, либо ре­зольвентой, можно сделать опровержение М, если оно является невы­полнимым. Такое опровержение называется опровержением М, имеющим множество поддержки Т. В системе резолюций, так же как и в естест­венной дедуктивной системе, можно при наличии ряда формул Г обра­батывать вопросы ряда формул B. Другими словами, если Г→В дока­зуемо, то ответом на вопрос является "да", а если доказуемо 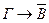, то ответом служит "нет". Стратегия приоритета простейшего предло­жения является самой эффективной среди стратегий общего назначения, но если простейшее предложение нельзя выбрать в качестве предпосыл­ки, то необходимо, чтобы предпосылкой было предложение с двумя и более литералами. Однако возникает вопрос, существует ли класс мно­жеств предложений, опровержимых просто путем выбора простейшего предложения хотя бы в качестве одной предпосылки? Ответ на этот воп­рос утвердительный. Такие множества называются хорновскими, а их элементы - хорновскими предложениями. Как было показано ранее, хорновское предложение содержит всего один правильный литерал. Други­ми словами, в таком предложении справа от стрелки либо может быть одна атомарная формула, либо ее нет. Резолюция, в которой хотя бы одна из предпосылок является простейшим предложением, называется простейшей резолюцией. Невыполнимость хорновского множества не толь­ко означает, что его опровержимость можно доказать с помощью прос­тейшей резолюции, но и показывает, что в процессе опровержения не требуется осуществлять факторизацию. Если типы предложений ограни­чить хорновскими, опровержение невыполнимого множества можно сде­лать очень эффективным. Однако даже хорновские множества нельзя наз­вать полными в смысле теоремы Геделя о полноте, т.е. существует та­кое множество хорновских предложений, которое нельзя опровергнуть, как нельзя опровергнуть и его отрицание. Однако благодаря простым механизмам вывода хорновское множество было предложено в качестве языка программирования. В результате был создан язык ПРОЛОГ.

КОМБИНАТОРНЫЙ АНАЛИЗ

 

При построении экспертных систем, систем автоматического выво­да имеется различное число вариантов научных решений конкретной проблемы, ближе или дальше отстоящих от оптимальною решения. Кроме того, целый ряд решений носит комбинаторно - логический характер. В общем случае при анализе модели предметной области производятся oпeрации над дискретными множествами, которые изменяют либо структуру множеств, либо их состав. Простейшими операциями первого типа яв­ляются обычные перестановки элементов, второго - выделение подмно­жеств элементов или, как принято говорить, их выборки. Операции при­меняют в задачах чаще всего неоднократно и в самых разнообразных комбинациях, при наложении различных условий. Это создает практи­чески неисчерпаемые возможности дискретных построений, которые не­редко называют конфигурациями (иногда комбинаторными конфигурация­ми) [22, 23].

В зависимости от характера предмета исследования и вводимых операций определяется совокупность задач, решаемых средствами ком­бинаторного анализа. Самыми первыми были задачи о числе дискретных построений, удовлетворяющих поставленным условиям. Метода их реше­ния получили название перечислительных. Кроме задач перечислитель­ного типа в комбинаторном анализа рассматриваются вопросы сущест­вования или несуществования конфигурации, удовлетворяющей заданным условиям, отыскиваются алгоритмы построения конфигураций, а также выделения из заданной совокупности конфигураций, или алгоритмов та­ких, которые обладали бы избранными свойствами в наибольшей или наименьшей степени (задачи и методы оптимизации) [24].

 

---

Дата добавления: 2018-11-24; просмотров: 450; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!