Динамика численности популяции в периодической среде.

Логистические модели популяционной динамики.

При анализе любой экологической системы главная проблема, которую приходится решать, — это выбор существенных переменных. Рассмотрим математические модели роста популяций, выбрав в качестве основных аргументов численность или плотность особей, и на этой основе будем исследовать соответствующую динамическую теорию устойчивости развития. Впервые такой подход использовал В. Вольтерра [17], и с тех пор его придерживается большинство экологов. (Плотность популяции ~ это величина (численность) популяции, отнесенная к единице пространства. Её обычно измеряют и выражают числом особей или биомассой популяции на единицу площади или объема, например, 700 деревьев на 1 га или 300 кг рыбы на 1 га поверхности водоема).

В этом разделе будут исследованы простейшие модели, описывающие изменения во времени только общей численности популяции N. При построении этих моделей все особи, составляющие популяцию, считаются совершенно идентичными, а величина численности принимается исчерпывающей характеристикой популяции как динамического объекта. Оказывается, что даже при таком сравнительно простом описании популяции можно построить модели, хорошо отражающие ряд экспериментальных фактов, касающихся развития популяций.

5.1. Однородная изолированная популяция в неизменной среде.

Биологические сообщества состоят из нескольких популяций биологических видов, живущих в общей среде. Обычно индивидуумы этих сообществ оспаривают одну и ту же пищу, или же одни виды живут за счет других, которыми они питаются. Они могут взаимно оказывать друг друзу помощь. Всё это входит в общее явление борьбы за существование. Количественный характер этого явления проявляется в заданной среде в виде изменений численности индивидуумов, составляющих разные популяции. При одних условиях эти изменения состоят из флуктуаций вокруг средних значений, при других условиях сводятся к исчезновению или прогрессирующему увеличению некоторых видов.

Для того чтобы охарактеризовать числом некоторую популяцию в рассматриваемой области, сделаем допущение, что все особи в популяции одинаковы и что тип индивидуума не меняется со временем. Будем также считать, что исследуемая популяция сосуществует с другими видами без прямого или косвенного взаимного влияния в неизменной среде, представляющей всегда одни и те же возможности максимально благоприятного существования для этой изолированной популяции.

Если вместо разрывных целочисленных функций, представляющих численность индивидуумов, ввести непрерывные дифференцируемые функции, имеющие в каждый момент времени ту же целую часть, что и разрывные, то для конечного интервала времени в достаточно многочисленной популяции число рождений и число смертей пропорциональны общей численности индивидуумов, существующих в данный момент. Если предположить, что численность популяции изменяется непрерывно, так что поколения перекрываются, а скорость прироста dN индивидуумов в некотором малом интервале времени dt пропорциональна численности N популяции, то, приписывая это свойство функции N=N(t), рассматриваемой как функция непрерывная, получим:

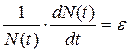(5.1.1)

где e— коэффициент, называемый относительной или удельной скоростью роста популяции, фактически представляющий собой разность между коэффициентом рождаемости В (т.е. скоростью рождаемости в единицу времени на одну особь) и коэффициентом смертности D, может быть выражен так:

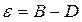(5.1.2)

Простейшая модель (5.1.1) была предложена Мальтусом (для роста населения Земли). Когда e = const > 0, эта модель ведёт к экспоненциальному (т.е. очень быстрому) росту численности N(t) с течением времени:

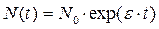(5.1.3)

где N₀ — численность популяции в начальный момент. Это хорошо известный закон Мальтуса - закон экспоненциального роста численности популяции в неограниченной среде. Такая динамика численности характерна для начальной фазы роста колонии бактерий, когда все необходимые для роста питательные вещества находятся в избытке.

Утверждение, что в неограниченной стационарной и благоприятной среде размер популяции экспоненциально возрастает, является одним из основных экологических принципов.

К счастью, экспоненциальный закон роста никогда не проявляется в полной мере благодаря воздействию окружающей среды (в благоприятных условиях потомство одной пары мух через несколько лет весило бы больше, чем земной шар).

Коэффициент относительной скорости роста e, называемый также коэффициентом прироста популяции, характеризует присущую живым организмам способность к увеличению численности в отсутствие лимитирующих факторов среды. Показатель e используется также для количественного выражения «репродуктивной приспособленности» в генетическом смысле. Величину e часто называют малътузианским параметром популяции.

Показатель роста e можно вычислить экспериментально по двум измерениям численности популяции на фазе нелимитируемого роста этой популяции. Если N₁ и N₂ - число индивидуумов популяции соответственно в моменты t₁ и t₂, то из (5.1.3) следует:

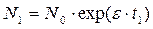
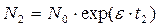
откуда

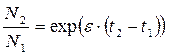
Логарифмируя получившееся равенство, получим уравнение в форме, удобной для проведения расчетов:

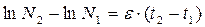откуда:

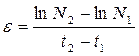(5.1.4)

Например, если за 10 лет наблюдения численность популяции возросла от 500 единиц до 600, то значение e = 0.0182.

При e > 0 уравнение (5.1.1) справедливо лишь для ограниченного периода времени. В природных условиях, где ресурсы, обеспечивающие рост, всегда ограничены, эффект безграничного экспоненциального роста не наблюдается. Всегда существует предельная численность К, которой может достигнуть популяция в условиях ограниченности ресурса (величину К обычно называют «ёмкостью» среды»). Заметим, что N стремится к К при t —> ¥. Когда численность популяции становится слишком большой, мальтусовская жёсткая модель с постоянным коэффициентом e перестаёт быть применимой. При слишком больших N конкуренция за ресурсы (пищу, пространство и т. п.) приводит к уменьшению e, и жёсткая модель Мальтуса должна быть заменена мягкой моделью с зависящим от N коэффициентом прироста популяции:

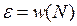
Первая модель, учитывающая этот факт, была предложена в 1825 г. Б. Гомпертцем:

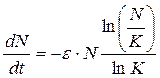
или, после интегрирования:

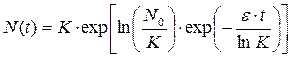
Как нетрудно заметить, эта модель описывает эффект «насыщения», но эксперименты с животными показали, что этот эффект наступает гораздо быстрее, чем следует из модели Гомпертца.

Например, при e = 0.0182, N₀ = 500, K = 600 по модели Гомпертца получим изменение численности во времени, представленной на рис. 5.1.1.

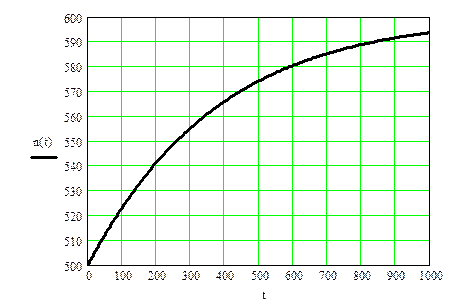Рис. 5.1.1. Изменение численности, рассчитанной по модели Гомпертца за период времени до 1000 лет.

5.2. Модель обобщенной логистической популяции.

К настоящему времени существует много популяционных моделей с различными законами локального роста. Если, например, предположить, что коэффициенты рождаемости B и смертности D в (5.1.2) могут зависеть от N, считая по-прежнему, что от пространственных координат B и D не зависят, то уравнение (5.1.1) с учетом (5.1.2) запишется в виде:

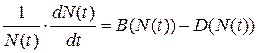(5.2.1)

где B(N(t)) и D(N(t)) — функции рождаемости и смертности, зависящие от численности популяции N(t) в данный момент времени.

Для многих видов функция рождаемости В(N(t)) определяется лишь физиологическими пределами рождаемости и не зависит от N(t), так что

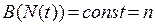, где n - это так называемая естественная рождаемость (или плодовитость) особи.

Что касается зависимости функции смертности D от N(t), то практически для всех популяций D(N(t)) — монотонно возрастающая функция, причем D(N(0)) = m> 0,где m— естественная смертность, а возрастание смертности с ростом N(t) объясняется ростом конкуренции за определённый ресурс (питание, пространство и т. п.).

Рассмотрим более подробно этот тип популяции. Наиболее простая форма зависимости D(N(t)) - линейная:

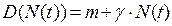
Тогда уравнение (5.2.1) принимает вид:

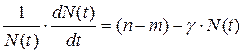
откуда, учитывая (5.1.2), имеем:

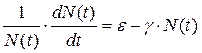(5.2.2)

где e = n-m - удельная скорость роста в отсутствие лимитирования;

g - коэффициент лимитирования, соответствующий потребности популяции в пище и называемый иногда «коэффициентом прожорливости»;

g×N(t) - слагаемое правой части уравнения (5.2.2) называют фактором тесноты. Это уравнение обычно записывают в виде:

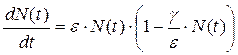(5.2.3)

и называют логистическим уравнением или логистической моделью.

Интегрируя логистическое уравнение при N(0)=N₀, получим:

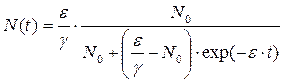(5.2.4)

Популяция с таким законом роста называется логистической.

Отметим некоторые свойства решения (5.2.4). Во-первых, из (5.2.4) следует, что

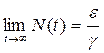(5.2.5)

т. е. численность популяции стремится к постоянной величине, которая прямо пропорциональна удельной скорости роста популяции в нелимитированной среде e и обратно пропорциональна коэффициенту лимитирования g. При этом возможны два случая: , .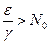

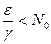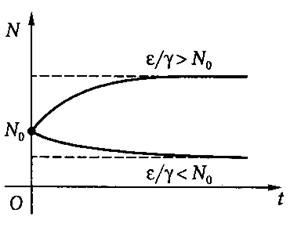
Рис. 5.2.1. Изменение численности логистической популяции.

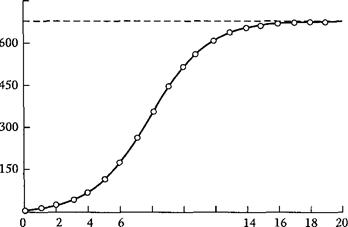
Различие между этими случаями хорошо видно из рис. 5.2.1. Отметим, что соотношение (5.2.4) описывает, в частности, популяции фруктовых вредителей и некоторых видов бактерий. Пример роста биомассы дрожжевых клеток в культуре и кривая роста, предсказанная логистическим уравнением, показан на рис. 5.2.2 .

Отношение (5.2.5) характеризует чувствительность вида к нехватке пищи: если дробь 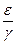мала, то вид очень чувствителен к нехватке пищи.

Во-вторых, из (5.2.4) следует, что при малых N₀ и конечном tимеем:

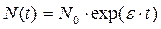
т. е. в популяции малой численности (когда отсутствует заметное влияние лимитирующих факторов) кривая изменения численности сходна с кривой динамики роста (5.1.3) в отсутствие лимитирующих факторов среды.

N(t)

время, ч.

Рис. 5.2.2. Кривая роста биомассы дрожжевых клеток.

Чтобы описать процесс роста населения США, в 20-х годах логистическую модель предложил Е. Перл (совместно с Ридом). Когда логистическая формула была опубликована, выяснилось, что ещё в 1838 г. она предлагалась бельгийским математиком Пьером Франсуа Ферхюльстом (1804 - 1849) для описания роста народонаселения. Эта простая и наглядная модель достаточно хорошо описывает динамику роста многих природных популяций. Широкое использование уравнения (5.2.3) связано с тем, что оно хорошо отражает начальный экспоненциальный рост популяции и асимптотическое приближение её численности к некоторому конечному значению, т. е. оно является простейшим дифференциальным уравнением, которое обладает следующими свойствами (рис. 5.2.3):

- при малых значениях N, пока популяция не исчерпала свои ресурсы (пищу или пространство), логистическое уравнение (5.2.3) сводится к уравнению (5.1.1) и возрастание N носит экспоненциальный характер;

- с возрастанием t растет N, ресурсы популяции уменьшаются, рост постепенно замедляется (фаза отрицательного ускорения), а N постепенно приближается к постоянному значению К = e/g.

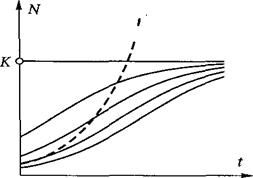Рис. 5.2.3. Логистическая модель с емкостью среды К= e/g.

Будем называть обобщенной логистической популяцией любую популяцию, локальный закон роста которой описывается уравнением:

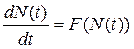(5.2.6)

где F(N(t)) удовлетворяет следующим условиям:

а)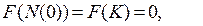

б) ;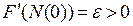

в)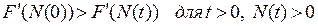

Для многих видов животных, способных мигрировать достаточно свободно и просторно заселяющих пространство обитания, предположение, что естественная рождаемость В(N(t)) = соп st не совсем верно, ибо при малых плотностях размножение определяется скорее вероятностью встречи брачных партнёров, а не физиологической плодовитостью.

Замечание.

В этом пункте при исследовании динамики численности изолированных популяций предполагалось, что все особи в популяции одинаковы и на внешние воздействия они реагируют мгновенно. Однако природные популяции не могут мгновенно реагировать на внешние воздействия, реакция на эти воздействия может происходить с некоторым запаздыванием. Например, у рыб это запаздывание соответствует интервалу между откладыванием икры и достижением потомством репродуктивной зрелости, а рождаемость травоядных даже в идеальных климатических условиях будет зависеть (из-за оскудения пастбищ) не только от текущей численности, но и от численности в прошлом, на интервале времени, приближенно равном периоду восстановления пастбища. Запаздывание может быть также обусловлено длительным достижением репродуктивного возраста и дискретностью сезонов размножения. Репродуктивные и другие запаздывания могут существовать одновременно.

Одна из первых математических моделей в биологии, учитывающих временные запаздывания, была предложена Дж. Эвелином Хатчинсоном (1903 - 1991), который первым среди экологов обратил внимание на важную роль запаздываний для динамики экосистем. Он рассмотрел уравнение:

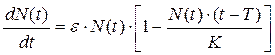, для Т>0, (5.2.7)

где К — максимально возможная стационарная численность популяции (ёмкость среды).

Популяционная модель (5.2.7) основана на следующих соображениях: по мере увеличения плотности какого-либо вида доступные ему ресурсы сокращаются; эта ситуация описывается логистическим уравнением (5.2.3). Однако в реальной экосистеме ресурсы способны к самовозобновлению, поэтому действительный уровень ресурсов, доступных в любой момент времени, будет зависеть от плотности ресурсного вида в некоторый момент времени (t –Т) в прошлом, где Т - «время развития» вида, служащего ресурсом. Таким образом, обычное (без запаздывания) логистическое уравнение (5.2.3) следует заменить уравнением (5.2.7). При наличии запаздываний численность популяции может колебаться: если Т велико относительно 1/e, то уравнение (5.2.7) приводит к расходящимся колебаниям. Вместе с тем логистические уравнение с Т= 0 всегда даёт устойчивое неколебательное равновесие.

Динамика численности популяции в периодической среде.

В п.5.1 решение (5.1.3) уравнения (5.1.1) получено в предположении, что относительная скорость роста численности N(t) популяции зависит только от величины e, характеризующей биологические особенности популяции, и не зависит от типа среды обитания, т. е.

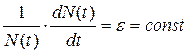
Однако в общем случае относительная скорость роста

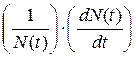характеризующая приспособленность популяции к среде обитания, будет зависеть не только от биологических особенностей самой популяции, но и от факторов среды обитания. В экологии принято разделять факторы среды обитания на факторы, интенсивность действия которых зависит от численности популяции, и факторы, не зависящие от этой численности. К факторам среды, не зависящим от численности популяции, относятся, например, метеорологические факторы: температура, химический состав среды, влажность и т. д.

К факторам, интенсивность действия которых зависит от численности, относят, например, обеспеченность популяции пищей, светом, водой и т. д.

Таким образом, количественной мерой относительной скорости роста численности популяции (мерой её приспособленности к среде обитания) будет функция вида

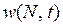
и, следовательно, уравнение динамики этого роста будет иметь вид

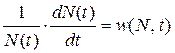(5.3.1)

Рассматривая величину приспособленности популяции 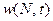как функцию от её численности N, можно построить классификацию типов зависимости приспособленности популяции от её численности. Пусть численность популяции, развивающейся в некоторой среде, увеличена в «с» раз. Что произойдёт с приспособленностью популяции 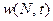? Разумеется, это будет зависеть от целого ряда обстоятельств: от обеспеченности популяции территорией, пищей и т. п.

Если все компоненты среды присутствуют в достаточном количестве, то увеличение численности не изменит величины приспособленности, т. е. в этом случае:

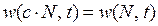(5.3.2)

Такой тип зависимости приспособленности от численности называют нейтральным, а популяцию соответственно — нейтральной.

Если в среде отсутствует в достаточном количестве хотя бы одна компонента, необходимая для жизнедеятельности популяции, то её недостаток будет лимитировать рост численности популяции, и тогда для функции 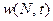при с >1 справедливо неравенство:

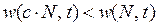(5.3.3)

Такой тип зависимости называют лимитирующим, а популяцию - лимитированной.

Помимо рассмотренных вариантов, возможна ситуация, когда увеличение численности в какие-то промежутки времени повышает приспособленность популяции. Явления такого рода имеют место, когда вступают в действие так называемые факторы «сотрудничества» особей, составляющих популяцию при освоении среды обитания. То, что это принципиально возможно, доказано экспериментально. В этом случае при с > 1 справедливо неравенство:

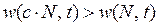(5.3.4)

Среда с такой величиной приспособленности называется стимулирующей.

Для получения дальнейших результатов следует установить явный вид функции приспособленности 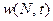, стараясь, чтобы это было по возможности простое выражение, включающее минимальное число параметров.

Сначала рассмотрим динамику численности популяции в нелимитированной нейтральной периодической среде. В этой среде величина приспособленности 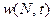от N не зависит и является периодической функцией времени t. Периодический характер изменения условий обитания необходимо учитывать при описании динамики численности популяций самых различных видов. Так, в динамике популяций млекопитающих большое значение имеют сезонные изменения погодных условий, для популяции насекомых — суточные колебания температуры и освещенности, для популяций прибрежных видов это могут быть изменения уровня воды, вызванные сменой приливов и отливов.

Пусть Т - период колебаний нелимитированной нейтральной периодической среды; в такой среде функция приспособленности 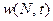имеет вид

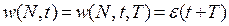(5.3.5)

где 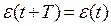для любых значений t.

Уравнение динамики численности популяции (5.3.1) запишется теперь следующим образом:

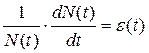(5.3.6)

Чтобы исследовать свойства решения уравнения (5.3.6), введём величину

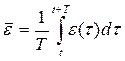, (5.3.7)

имеющую смысл средней скорости изменения численности популяции за период Т, и вспомогательную функцию j(t), определив её равенством:

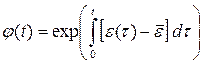(5.3.8)

Покажем, что в силу (5.3.7) функция j(t) периодична и имеет тот же период Т, что и функция e(t). Действительно, учитывая, что :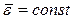

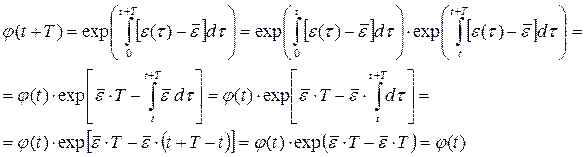
Найдём теперь решение уравнения (5.3.6). Проинтегрировав его при N(0)=N₀ с последующим потенцированием, получим:

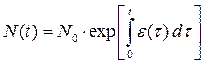(5.3.9)

где N₀ - численность популяции в начальный момент времени t = 0. Из (5.3.9) в силу определения (5.3.8) функции j(t) следует:

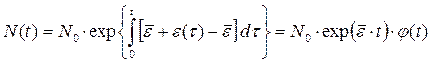
Т.е. изменение численности популяции в нейтральной периодической среде запишется в виде произведения экспоненты с показателем роста 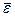и некоторой положительной периодической функции j(t):

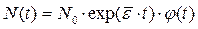
Если 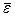>0, т.е. положительна средняя скорость изменения численности (средний показатель роста), то численность популяции растёт бесконечно, колеблясь около экспоненты с показателем .

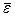Если 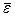=0, то численность популяции периодически меняется около некоторого постоянного уровня.

Если 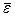< 0, то численность популяции стремится к нулю с ростом времени, колеблясь около убывающей экспоненты.

Отметим, что при 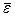= 0 среднее значение численности популяции 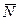за рассматриваемый период времени, вообще говоря, не равно N₀:

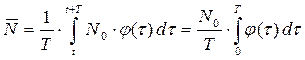
Отсюда следует, что периодичность изменения среды обитания популяции приводит не только к колебаниям численности, но в зависимости от формы этой периодичности может сдвигать средний уровень численности как в меньшую, так и в большую сторону от её начального значения. При этом, как уже отмечалось ранее, бесконечный рост численности популяции не имеет непосредственного биологического смысла, это является лишь идеализированной моделью реальных процессов, протекающих в популяции на фазе нелимитируемого роста.

Исследуем популяцию, динамика роста которой описывается логистическим уравнением в нестационарной среде. В этом случае удельная скорость роста e и коэффициент лимитирования g в уравнении (5.2.2) будут уже не параметрами, а функциями от t, и уравнение принимает вид:

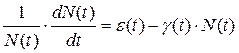
Это уравнение (известное как уравнение Бернулли) относительно неизвестной функции N(t) может быть записано в виде:

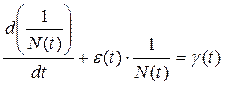(5.3.10)

Уравнение (5.3.10) будет линейным уравнением относительно неизвестной функции 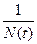, и его решение может быть записано в форме:

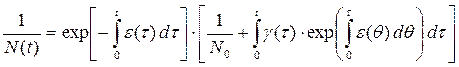откуда:

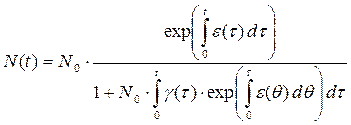(5.3.11)

Пусть нестационарная среда обитания логистической популяции будет периодической и Т - период колебаний этой среды, тогда

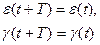
при всех значениях t.

В этом случае формула (5.3.11) может быть записана следующим образом:

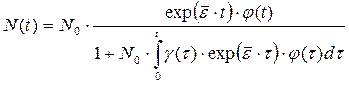(5.3.12)

где `e - средняя относительная скорость изменения роста популяции за период T в отсутствие лимитирования, определяемая по формуле (5.3.7), а j(t) - положительная периодическая функция периода T, определяемая формулой (5.3.8). Если 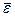> 0, то в нестационарной периодической среде обитания закон изменения численности логистической популяции с течением времени стремится к периодической кривой с периодом Т.

Следует заметить, что рассмотренная простая логистическая модель, описывающая динамику развития не только экологической системы, опасна при планировании развития системы в рациональном варианте, т.е. при оптимизации параметров системы. Такая «оптимизация» может приводить к полному уничтожению системы вследствие возникающей из-за оптимизации неустойчивости решений.

Дата добавления: 2018-10-27; просмотров: 1095; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!