Теория Аббе разрешающей способности микроскопа
Лекция Дифракция
Принцип Гюйгенса. Интеграл Кирхгофа. Под дифракцией принято называть оптические эффекты, которые не могут быть объяснены с позиций геометрической оптики. В частности, под дифракцией подразумеваются явления, при которых свет отклоняется от прямолинейного распространения. Одним из примеров дифракции является проникновение света за границу тени от непрозрачной преграды (рис. 1А). Однако наличие преграды не является обязательным. Пример – лазерный пучок распространяется так, что его каустики представляют собой гиперболы (рис. 2Б).
Дифракцию можно объяснить с помощью принципа Гюйгенса – Френеля, который является следствием уравнений Максвелла. Такое объяснение не является единственным, но его достоинство заключается в наглядности, к тому же основные положения этого принципа были сформулированы еще до получения уравнений Максвелла.
Суть принципа заключается в следующем. Каждая точка волнового фронта является точеным источником вторичной сферической волны, при этом его комплексная амплитуда 
равна комплексной амплитуде исходной волны в данной точке. Комплексная амплитуда поля в произвольной точке пространства будет суммой комплексных амплитуд всех вторичных волн, т.е. их интерференции, в этой точке. Таким образом, принцип Гюйгенса позволяет определить распределение амплитуд и, соответственно, распределение освещенности во всех точках пространства, т.е. получить исчерпывающую характеристику электромагнитного поля.
|
|
|
Получим математическую запись этого принципа. Зададим некоторую поверхность 
, через которую проходит исходная волна. Определим связанную с ней систему координат 
. Через произвольную точку пространства 
, в которой требуется определить амплитуду поля, проведем плоскость 
, параллельную координатной плоскости 
и определим в ней систему координат 
так, что ее оси были параллельны соответствующим осям 
. Возьмем на произвольную точку 
с координатами 
, при этом 
, где 
- уравнение поверхности . Согласно вышеизложенному, в ней находится точечный источник с комплексной амплитудой
 ,
| (1) |
где 
и 
[1] - амплитуда и фаза падающей волны в этой точке. Уравнение сферической волны, вышедшей из в точке с координатами 
будет
 ,
| (2) |
где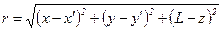 
радиус сферы, в данном случае равным расстоянию между точками и , 
- расстояние между началами координат и . Таким образом комплексная амплитуда волны в точке , вышедшей из точки будет
 .
| (3) |
Полная амплитуда в точке есть сумма амплитуд сферических волн от всех вторичных источников, т.е. интеграл
|
|
|
 ,
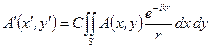| (4) |
где 
- область поверхности , в которой расположены вторичные источники.
Полученное выражение представляет собой дифракционный интеграл в приближении Кирхгофа. Вычисление этого интеграла позволит решить поставленную задачу – по заданному значению поля на некоторой поверхности определить амплитуду электромагнитного поля в любой точке пространства.
Однако вычисление этого интеграла сопряжено с большими трудностями. Прежде всего, существует крайне мало функций 
, для которых результат интегрирования выражается через конечное число функций, т.е. представим в аналитическом виде. Кроме того, использование вычислительных средств приводит к недопустимо большим затратам машинного времени. Это происходит из-за осциллирующего характера подынтегральной функции. Дело в том, что сомножитель 
, который в силу формулы Эйлера выражается через синус и косинус, аргументы, которых содержат большое число (например, для 
). Такая функция будет менять знак через 0.63 мкм и при интегрировании (к примеру) по квадратной площадке 10 
10 мм число перемен знака у подынтегральной функции будет порядка 
. Для получения хотя бы примерного результата необходимо эту цифру умножить минимум в 6 раз, поскольку большинство алгоритмов интегрирования вычисляют площадь под кривой (в данном случае объем под поверхностью). Надо сказать, что существуют специальные алгоритмы вычисления таких интегралов, время выполнения которых существенно меньше, но все равно затраты времени недопустимо высоки.
|
|
|
Тем не менее, попытки вычисления таких интегралов предпринимались, и первая оценка его величины была осуществлена Френелем с помощью так называемого методом зон Френеля. Он достаточно хорошо изложен в курсе физики, поэтому напомним лишь его основную идею и выводы. Суть его заключается в следующем. Сферический волновой фронт, исходящий из точечного источника , на котором располагаются вторичные источники, разбивается на ряд концентричных оси зон так, чтобы разность хода от середин двух соседних зон равнялась половине длины волны (рис. 3).
| (5) |
Доказывается, что площади этих зон почти равны, поэтому световые потоки от вторичных источников в этих зонах почти равны и так как в соседних зонах они в противофазе, в точке 
эти потоки взаимно уничтожаются. Таким образом, если рассматривать дифракцию на отверстии, то если на нем помещается четное число зон, то в точке будет минимум освещенности, а если четное, то максимум. Радиус 
зоны 
Френеля вычисляется по формуле
|
|
|
 ,
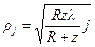| (6) |
где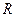 
- расстояние по оси от источника до отверстия; 
- расстояние от отверстия до точки наблюдения . Если источник в бесконечности, т.е. на отверстие освещается параллельным пучком, то выражение (6) упрощается
 .
| (7) |
С помощью зон Френеля легко объясняется дифракционный эффект, называемый пятном Пуассона. Если на пути параллельного пучка лучей поместить препятствие так, что его размер будет равен первой зоне Френеля, то согласно вышеизложенному, в точке будет максимум освещенности, т.е. яркое пятно (рис. 4). Это противоречит геометрической оптике, поскольку точка находится в центре тени от препятствия. Это эффект можно использовать для определения границы применения приближения геометрической оптики – если соотношение между размером препятствия 
, расстояния от него и длиной волны излучения таковы, что размер препятствия порядка первой зоны Френеля, т.е.
 ,
| (8) |
то необходимо учитывать волновые свойства света - приближение геометрической оптики в данном случае неправомерно.
Дифракционные приближения. Дифракционные интегралы. Отмечалось, что дифракционный интеграл Кирхгофа неудобен для вычислений. Напомним, что физически этот интеграл представляет сумму вторичных сферических волн. Однако волновые свойства свет проявляет, в основном, в пучках с малой расходимостью, т.е. в узких пучках. В противном же случае аберрационные эффекты значительно сильнее волновых и вычисление дифракционных интегралов теряет смысл. Таким образом, на практике необходимо учитывать лишь небольшую часть сферических волновых фронтов вторичных волн. Это обстоятельство позволяет существенно упростить дифракционный интеграл и придать ему вид, значительно более удобный для практического использования. Таким образом, необходимо рассматривать такую геометрию распространения света, когда характерный размер объекта, на котором происходит дифракция 
и размер области, где она наблюдается 
, значительно меньше расстояния между ними (рис. 5), т.е.
 .
| (9) |
Выберем в качестве поверхности вторичных источников плоскость ( 
и используя соотношения (9), преобразуем выражение для 
с помощью разложения 
для 
 .
| (10) |
Тогда для экспоненты
| (11а) |
где 
, но для в знаменателе
 ,
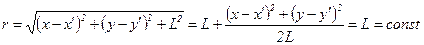| (11б) |
в силу соотношений (9).
Объединяя константы в (11а) и (11б) в одну, запишем интеграл в виде
 .
| (12) |
Полученное выражение называется дифракционным интегралом в приближении Френеля, а условия, когда такое приближение справедливо, иногда называют волновой зоной. Геометрически это приближение означает замену сферы параболоидом вращения. Этот интеграл значительно проще. В частности, если 
, то переменные в подынтегральном выражении разделяются и двукратный интеграл заменяется произведением двух однократных, что приводит к принципиальному упрощению.
При дальнейшем уменьшении угла расходимости пучка, или что эквивалентно усилению соотношения (9), можно считать, что в формировании дифракционной картины участвует такая малая часть сфер вторичных волн, что эти волны можно считать плоскими. Математически это означает, что в показателе экспоненты подынтегрального выражения можно пренебречь квадратами переменных и интеграл (12) примет вид
 .
| (13) |
Этот интеграл называется дифракционным интегралом в приближении Фраунгофера, а условия его выполнения называют дальней зоной. Необходимо отметить, что условия приближения Кирхгофа называются ближней зоной.
Интегралы (12) и (13) представляют собой так называемые интегральные преобразования, так как они ставят в соответствие функции функцию 
, при этом (12) является преобразованием Френеля, а (13) – преобразованием Фурье. Выражение (13) представляет собой сумму плоских наклонных волн с углами (рис.5)
 и  .
| (14) |
Если дифрагирующий объект поставить перед линзой с фокусным расстоянием 
, то все лучи с углами наклона (14), т.е. параллельные между собой, соберутся в фокальной плоскости в точке с координатами в фокальной плоскости 
и 
, определяемые соотношениями
 и  .
| (15) |
Комбинируя (14) и (15) и подставляя результат в (13) интеграл можно записать как
 .
| (15) |
где 
, 
. Величины 
и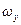 
носят названия пространственных частот. При таких обозначениях выражение (15) формально совпадает с выражением для спектрального разложения электрических сигналов. Оказывается, что эта аналогия далеко не формальна и выражение (15) лежит в основе Фурье – оптики и оптической обработки информации. Таким образом, дифракцию Фраунгофера можно наблюдать в фокальной плоскости линзы (рис. 6). Заметим, что волновой фронт в фокальной плоскости плоский. Вблизи фокальной плоскости выполняются условия дифракции Френеля и вдали от нее – условия для дифракции Кирхгофа. Видно, что отклонения от геометрической оптики в случае дифракции Кирхгофа минимальны. Этот рисунок иллюстрирует неприемлемость приближения геометрической оптики вблизи фокальной плоскости – если луч определить как нормаль к волновому фронту, то вблизи линзы луч наклонен к оси, а в фокальной плоскости он ей параллелен. Таким образом, наблюдается отклонение от прямолинейного распространения.
Так как размер дифракционной картины мал, то ее удобно наблюдать через окуляр. Такая двухкомпонентная система является зрительной трубой (рис.6).
Примеры дифракции
Дифракция на прямоугольном отверстии и щели. Рассмотрим дифракцию на прямоугольном отверстии. Для расчета распределения освещенности в фокальной плоскости необходимо воспользоваться дифракционным интегралом в приближении Фраунгофера
| (1) |
| (2) |
где 
- прямоугольная область 
(рис. 1). Полагая, что отверстие освещается параллельным пучком с равномерным распределением освещенности 
, запишем двойной интеграл как повторный, который вычисляется без труда
Распределение освещенности 
получится возведением в квадрат (2). Выбирая 
так, чтобы 
, запишем выражение для 
 ,
| (3) |
где 
; 
- здесь пространственные частоты 
и 
выражены через координаты в фокальной плоскости 
и 
. Из (3) следует, что распределение освещенности есть произведение двух аналогичных функций, каждая из которых есть функция только одной координаты. Из очевидных равенств 
и 
следует, что каждая из них есть сечение двумерной функции распределения. Исследуем, для определенности первое из них. График этой функции приведен на рис 2. Нули, они же и минимумы, можно найти из условия 
откуда
| (5) |
так как из 
следует, что 
, и в выражении (4) возникает неопределенность типа 
, представляющая собой замечательный предел, равный 1. Именно этим объясняется глобальный, главный максимум при 
. Выражения для минимумов 
получатся из (5)
 .
| (6) |
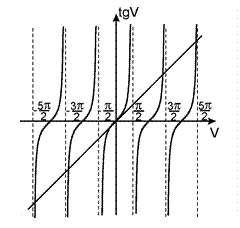Остальные максимумы, называемые побочными, можно определить из условия 
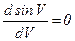. Вычисляя производную, найдем уравнение
для максимумов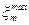 
 ,
| (7а) |
откуда
 .
| (7б) |
Полученное уравнение не имеет аналитического решения, но результат можно получить графически (рис.3). Из этого рисунка видно, что ординаты точек пересечения близки к 
и при 
стремятся к этим значениям. Таким образом, можно считать, что положения точек максимумов 
примерно равны
 .
| (8) |
 .
| (9) |
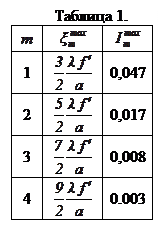Примерные значения освещенности в максимумах можно определить комбинирую соотношения (3), (7б) и (8). Учитывая равенство 
, получим
Зависимость интенсивностей побочных максимумов относительно интенсивности главного максимума приведена в таблице 1.
Если рассматривать двумерную картину дифракции, то из выражений для максимумов и минимумов (5) и (8), расстояние между побочными максимумами обратно пропорциональны ширине прямоугольного отверстия в этом направлении, т.е. дифракционная картина как бы растягивается в стороны больших сторон прямоугольника и, соответственно, сжимается со стороны меньших (рис. 4а). При дифракции на щели, которую можно считать таким прямоугольным отверстием, у которого одна из сторон значительно меньше другой, дифракционная картина вытягивается в тонкую линию (рис. 4б).
Дифракция на круглом отверстии. Учет дифракции на круглом отверстии имеет большое значение, так как подавляющее большинство оптических приборов имеет оптические элементы круглой формы. Для определения распределения освещенности в дифракционной картине поступим аналогично предыдущему случаю и вычислим дифракционный интеграл Фраунгофера, но областью интегрирования здесь будет круг заданного радиуса 
.
 .
| (10) |
Удобно перейти в полярную систему координат
| (11) |
тогда 
, 
и интеграл (10) примет вид
 .
| (12) |
Внутренний интеграл выражается через функцию Бесселя
 ,
| (13) |
где 
- функция Бесселя нулевого индекса. Полный интеграл получится в результате интегрирования по 
, который сводится к табличному интегралу от функции Бесселя. Результат интегрирования не зависит от угловой переменной 
 ,
| (14) |
где 
- функция Бесселя первого индекса.
График сечения функции 
приведен на рис. 5. Внешне он похож на сечения распределения при дифракции на прямоугольном отверстии. Но так как аргументом этой функции является 
, то дифракционная картина будет состоять из концентрических окружностей и внешне напоминать кольца Ньютона. Однако между этими распределениями есть существенные отличия – у колец Ньютона расстояния между кольцами убывают пропорционально корню квадратному их номера[2], а в рассматриваемом случае эти расстояния стремятся к постоянной величине. Кроме того зависимости интенсивностей колец от их радиусов существенно отличаются. Распределения интенсивностей при дифракции на круглом отверстии называется распределением Эри. Минимумы функции определяются нулями функции Бесселя 
, значения которых совместно с радиусами темных колец сведены в таблицу 2. Туда же внесены и значения максимумов распределения совместно с радиусами светлых колец, которые получены из условия равенства нулю производной, которая равна 
, откуда 
получаются из условия 
, где 
функция Бесселя второго индекса.
Таблица 2.
| Светлые кольца | Темные кольца | |||||
| № |
| 
| 
| № | 
| 
|
| 1 | 5.135 | 0.817 
| 0.01752 | 1 | 3.832 | 0.6098 
|
| 2 | 8.417 | 1.340
| 0.00415 | 2 | 7.016 | 1.117
|
| 3 | 11.620 | 1.849
| 0.00161 | 3 | 10.173 | 1.619
|
| 4 | 14.796 | 2.355
| 0.00078 | 4 | 13.324 | 2.121
|
По сравнению с дифракцией на прямоугольном отверстии интенсивность побочных максимумов здесь меньше.
Дифракция на периодической структуре. Рассмотрим дифракцию на одномерной периодической структуре, называемой еще решеткой. Пусть ее пропускание описывается комплексной, периодической с периодом 
в направлении оси 
, а в направлении 
- постоянной функцией 
, т.е.
| (8) |
Предположим, что на решетку падает световая волна с постоянной амплитудой 
и плоским волновым фронтом в направлении нормали к решетке. Распределение поля после решетки будет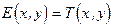 
. Если решетка имеет ширину (в направлении оси ) 
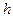, а длину 
, где 
- число элементов решетки (будем считать, что длина решетки в точности равна целому числу элементов), то дифракционный интеграл в этом случае примет вид
| (9) |
где 
- область, занимаемая решеткой (область интегрирования), а в постоянную 
включено значение амплитуды падающего света 
. Так как 
не зависит от 
, то по можно выполнить интегрирование (вынести множитель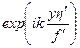 
за знак интеграла по 
, после чего интеграл по вычисляется без труда). Включив результат интегрирования по в 
, которая будет зависеть только от 
, запишем (9) в виде однократного интеграла
 .
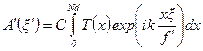| (10) |
Разбивая область интегрирования на отрезки длиной периода 
, запишем интеграл (10) в виде суммы
 .
| (11) |
Используя периодичность функции 
(рис. *), выражение (11) можно записать как
 .
| (12) |
 .
| (13) |
Это выражение можно преобразовать, используя теорему смещения, которая очень легко доказывается с помощью замены переменной интегрирования
Применяя, получим
| (14) |
где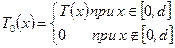 
.
Выражение в квадратных скобках представляет собой геометрическую прогрессию. Суммируя ее, получим
 .
| (15) |
Так как фиксируется лишь интенсивность электромагнитного поля, то для ее определения необходимо взять квадрат модуля (14)
 ,
| (16) |
где 
- так называемая структурная функция решетки, представляющая собой распределение освещенности в дифракционной картине от одного элемента структуры.
Из (16) следует то, что распределения всех периодических структур имеют общий характер, описываемый множителем перед интегралом, а конкретный вид распределения определяется выражением 
. График зависимости 
приведен на рис(16). Он может быть получен умножением графика 
на график структурной функции 
, который является для 
огибающей. Построим график 
. Введем безразмерную переменную 
, т.е. будем исследовать зависимость
| (17) |
Данная формула представляет собой отношение двух периодических функций, причем период знаменателя 
, а период числителя в 
раз меньше, т.е.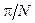 
. Из теории периодических функций, известно, что их отношение также будет периодической функцией с наибольшим у этих функций периодом 
.
Знаменатель обращается в нуль при
 .
| (19) |
 ,
| (18) |
где 
- целое число, однако в этих точках и числитель обращается в нуль, т.е. в этих точках возникает неопределенность типа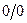 
. Раскрывая ее по правилу Лопиталя, найдем, что значение функции в этих точках равно 
. Так как 
, то минимум функции тогда, когда 
, т.е. при 
, т.е. при
Числитель функции осциллирует значительнее чем знаменатель, то можно считать, что 
будет иметь также максимумы приблизительно в тех точках, когда 
, т.е. при
. (20)
Значения в этих точках будут 
и при больших значениях (это можно доказать) 
т.е. их величины значительно меньше, чем у максимумов, положения которых определено (18).
Таким образом, рассматриваемая функция будет иметь главные максимумы, в точках, определяемых условиями
, (21.а)
откуда положения главных максимумов
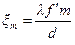. (21.б)
По аналогии определим положения максимумов 
. Они называются побочными (из (20))
(22)
и минимумов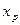 
. (23)
Из анализа выражений (21) - (23) следует, что между двумя главными максимумами находится 
побочных максимума, разделенных 
минимумами, так как расстояние между побочными максимумами в раз меньше, чем между главными. График этой функции показан на рис 2 а.
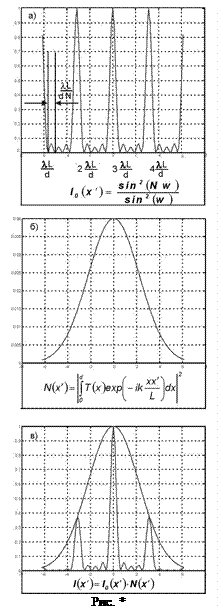
Структурная функция, как уже отмечалось, представляет собой дифракционное распределение интенсивности от одного элемента периодической структуры. Это значительно более плавно изменяющаяся функция и ее примерный вид показан на рис 2 б. Наконец, дифракционное распределение от всей структуры показано на рис 2 в и получено как произведение двух верхних графиков.
Из сказанного ясно, что основным параметром, характеризующим дифракционную структуру, является ее пространственный период 
, именно от него зависят положения главных максимумов. Все остальные параметры дифракционного распределения играют второстепенную роль. Параметр носит название постоянной решетки.
Рассмотрим плоскую одномерную амплитуднуюдифракционную решетку или, просто дифракционную решетку. Она состоит из ряда прозрачных прямоугольных отверстий шириной 
и шириной непрозрачной части 
так, что 
. Согласно (16), влияние этих параметров скажется через структурную функцию решетки, для чего надо вычислить интеграл
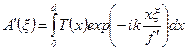, (24)
где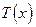 
- функция пропускания одного элемента решетки.
. (25)
Этот интеграл представляет собой дифракцию на прямоугольном отверстии и его вид нам известен
. (26)
Его вид приведен на рис 5, а нули 
выражаются формулами 
. После определения квадрата модуля полученного выражения и подстановки его в (16), распределение освещенности в дифракционной картине примет вид
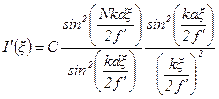
| (27) |
Распределение освещенности от решетки с 
показан на рис 8. Так как ширина структурной функции обратно пропорциональна размеру прозрачной части штриха , то решетке присуще некоторое противоречие: при уменьшении - с одной стороны все большее число главных максимумов имеют достаточно большую амплитуду, а с другой - через решетку проходит меньше света. Это особенно важно при использовании дифракционной решетки в качестве диспергирующего элемента в спектральных приборах - в них используется зависимость положения главных максимумов от 
и эта зависимость пропорциональна номеру (порядку) главного максимума. Возможны ситуации, когда минимумы структурной функции совпадают с главными максимумами. Рассмотрим условия их возникновения. Минимумы структурной функции возникают при 
, т.е. при 
. Сравнивая это выражение с (18), найдем, что это совпадение выполнится при 
. Именно такой случай представлен на рис 4, где третий главный максимум подавлен вторым минимумом структурной функции.
Применение дифракции.
Оценка качества изображения на базе теории дифракции.
Одним из главных вопросов, решаемых с помощью теории дифракции, является оценка качества изображения. Дифракционная природа изображения определяет одну из важнейших характеристик оптических систем – разрешающую способность. Если оптическая система обладает большими остаточными аберрациями, то оценка качества системы сводится к определению этих аберраций, точные значения которых можно найти тригонометрическим расчетом лучей, или приближенно, используя теорию аберраций третьего порядка. Если аберрации настолько малы, что систему можно считать безаберрационной, то все искажения, вносимые ею, будут следствием волновой природы света - дифракцией, которая возникает на материальных преградах в оптической системе. Такие системы называются дифракционно ограниченными. Доказано, что в любой оптической системе такая материальная преграда обязательно присутствует и ею является апертурная диафрагма. Именно на ней и происходит дифракция, в результате чего волновой фронт от предмета деформируется, что и приводит к ухудшению качества изображения. На практике иногда удобнее использовать изображения апертурной диафрагмы – входной или выходной зрачок.
Критерий Релея.
Оценим разрешающую способность телескопа или зрительной трубы. В этих приборах апертурной диафрагмой и одновременно и входным зрачком является оправа объектива. Поскольку оправа объектива является отверстием диаметра 
, то распределение освещенности в дифракционной картине в плоскости полевой диафрагмы (плоскости промежуточного действительного изображения) имеет осевую симметрию и описывается с помощью функции Бесселя 
(28)
где 
, 
- радиус оправы объектива (выходного зрачка), 
, 
и 
- координаты в плоскости полевой диафрагмы, 
- длина волны излучения, 
фокусное расстояние объектива. Таким образом, в этой оптической системе каждая точка предмета будет отображаться распределением (28) – дифракционным распределением Эри и будет иметь вид, показанный на рис. 9. Таким образом, детали изображения объекта меньшие, чем показанное распределение, будут отображаться с искажениями. Эти искажения будут зависеть от соотношения размеров изображаемых деталей и дифракционного распределения. Таким образом, что бы определить порог допустимых искажений, вводится понятия "разрешающей способности оптической системы", которое определяет условия, когда система формирует изображение удовлетворительного качества. Характеристики полученного изображения и определяют этот порог.
Впервые понятие разрешающей способности ввел Релей, именно для астрономических телескопов. Им была предложена следующая количественная оценка разрешения - точки (изображения звезд) считаются оптически разрешимыми, если главный максимум в дифракционном распределении освещенности изображения одной звезды совпадает с первым минимумом распределения в изображении соседней. Вид такой дифракционной картины приведен на рис.10. Сечение ее энергетического профиля по оси симметрии приведено на рис. 11. Из вида дифракционного изображения и его энергетического сечения следует, что кривая, описывающая это сечение, имеет провал, освещенность в котором составляет на 22% от освещенности в максимуме. Изложенный способ определения разрешающей способности оптической системы носит название критерий Релея. Однако в зависимости от приемника излучения можно зафиксировать разницу в освещенностях меньшую, чем в этом критерии и тем самым "улучшить" разрешающую способность. Например, человеческий глаз способен определить разницу в освещенностях порядка 10%, а фотодетекторы и того меньше. Таким образом, критерий Релея является относительной оценкой качества изображения.
Определим разрешающую способность телескопа по критерию Релея в зависимости от его конструктивных параметров. Схема телескопа (без окулярной части) приведена на рис.12.
Наблюдаемые в телескоп астрономические объекты – звезды находятся на огромных расстояниях и их вполне можно считать точечными источниками в бесконечности, излучение от которых попадает на объектив в виде плоских волн. Пусть угловое расстояние между наблюдаемыми звездами составляет 
радиан. Тогда в задней фокальной плоскости объектива будут два дифракционных изображения звезд в виде распределений Эри (28) и рис. 10, расстояние между которыми 
составит (с учетом малости угла ).
 .
| (29) |
В соответствии с критерием Релея звезды будут различимы как два объекта, если расстояние между их изображениями будет больше или равно радиусу первого темного кольца 
распределения Эри. Функция этого распределения описывается выражением (28) и радиус отмеченного выше кольца равен значению первого нуля функции Бесселя 
, т.е. из 
следует, что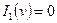 
. Значение 
известно, откуда радиус первого кольца будет как
 .
| (30) |
где 
- радиус оправы объектива, - ее диаметр, - длина волны излучения, - фокусное расстояние объектива.
Отсюда минимальное расстояние между изображениями, которое можно зафиксировать согласно критерию Релея, равного первого кольца распределения будет
 .
| (31) |
В угловых единицах значение разрешения 
будет
 .
| (32) |
Из выражения (32) можно получить формулу для предельного углового разрешения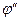 
, удобную для практического использования. Переходя из радиан в угловые секунды и полагая длину волны 
, близкой к максимальной спектральной чувствительности глаза, и подставляя в (32) получим
 ,
| (31) |
где 
- число угловых секунд в радиане, - диаметр объектива в миллиметрах.
Следует отметить, что критерий Релея используется не только для оценки качества телескопов и зрительных труб. По этому критерию определяют разрешение интерферометров, спектральных приборов и многих других оптических приборов. Критерий Релея является наиболее распространенным.
Критерий Штреля.
Другой, часто используемой оценкой качества изображения, является критерий Штреля. Суть его заключается в следующем. Для идеальной оптической системы (в смысле безаберрационной), распределение в изображении точки является распределением Эри. В этом случае, если максимальную освещенность в центральном максимуме принять за 100%, то в первом максимуме будет 1.75%, во втором 0,16% и т.д. При этом при визуальном наблюдении в дифракционной картине заметны лишь одно, максимум два - три кольца. В реальных оптических системах, вследствие технологических недостатков или аберраций, дифракционное изображение точки будет меняться и по его виду можно судить о качестве такой системы. Например, при наличии в системе сферической аберрации вид распределения в изображении точки будет таким же, как и при дифракционном, но яркость колец возрастет, а центрального максимума уменьшится. Другими словами произойдет перекачка энергии света в кольца. Это означает, что среднестатистический радиус[3] изображения точки, называемого радиусом пятна рассеяния, увеличится, что ухудшит качество изображения. При других аберрациях возникают иные деформации, а в случае сильных аберраций изображение точки является просто пятном, в котором отсутствуют участки с нулевой освещенностью.
Это возникает по следующей причине. Входной зрачок оптической системы можно разбить на зоны 
, аберрационные искажения в которых меньше дифракционных рис.13. Релей показал, что это наступает, когда деформация волнового фронта на краю зоны отличается от идеального волнового фронта не более чем на 
. Для каждой такой зоны возникает свое дифракционное распределение, зависящее от формы этой зоны. Так как фазы волновых фронтов от каждой зоны отличаются друг от друга случайным образом, то они не интерферируют, а складываются по интенсивности. Суммарная картина имеет вид, показанный на рис.14. Из этого рисунка видно, что площадь и пропорциональная ей энергия дифракционной, изрезанной части изображения соотносится ко всей площади, как площадь безаберрационной зоны 
к площади входного зрачка 
.
Теория Аббе разрешающей способности микроскопа
 |
Определение разрешающей способности по Аббе основано дифракционной структуре изображения в микроскопе. Это справедливо по следующим причинам – как правило, объективы микроскопов корректируются до уровня, когда аберрациями можно пренебречь. Во-вторых, изучаемые с помощью микроскопов объекты сравнимы с длиной волны, и волновыми свойствами света пренебречь нельзя и, наконец, освещение объектов можно считать с достаточной степенью когерентным, в силу теоремы Цернике[4]. Аббе было предложено в качестве тестовых объектов для микроскопов использовать периодические структуры. Это оправдано тем, что с точки зрения Фурье-анализа любую функцию, стремящуюся к нулю в бесконечности, можно представить как сумму бесконечного числа тригонометрических функций с периодами, величины которых составляют непрерывную последовательность, т.е. в виде интеграла Фурье. Ясно, что структура с таким минимальным периодом, который будет еще отображаться микроскопом, определит минимальный размер разрешаемой детали объекта, поскольку она будет одного порядка с этим периодом. Таким образом, предложенная Аббе методика вполне адекватна. Необходимо отметить, что эта идея Аббе оказалась весьма плодотворной, и ее развитие привело к появлению таких разделов оптики как теория распознавания образов и Фурье-оптика.
На рис.15 показан объектив микроскопа 1, а предметом является синусоидальная структура 2 с периодом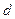 
, функцию пропускания которой можно представить 
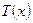как
 ,
| (32) |
где 
- координата в плоскости изображения, "единица" добавлена как опорное (среднее) значение освещенности, так как освещенность отрицательной быть не может.
В силу предположения о когерентности освещения объекта, в задней фокальной плоскости объектива сформируется картина дифракции Фраунгофера от синусоидальной структуры, распределение освещенности в которой будет иметь вид, показанный на рисунке. График этого распределения может 
быть получен в результате вычисления дифракционного интеграла в приближении Фраунгофера
 ,
| (33) |
где 
- часто употребляемая сокращенная запись функции;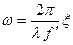 
- т.н. пространственная частота, величина, пропорциональная координате 
в фокальной плоскости; - фокусное расстояние объектива; 
; 
. (Данный интеграл легко вычисляется, если воспользоваться формулой Эйлера 
). Функция 
исследовалась при анализе дифракции на пря 
моугольном отверстии, а график выражения (33) имеет вид, показанный на рис. 16. Каждый из боковых максимумов представляет собой сфокусированную плоскую дифрагированную структурой волну. В соответствии с принципом Гюйгенса-Френеля они являются источниками вторичных волн, интерференция которых сформирует изображение объекта – периодическую структуру 
. Покажем это. Данная ситуация аналогична той, которая возникает в опыте Юнга – здесь также происходит интерференция сферических волн, но исходящих от трех точечных источников, расположенных симметрично оптической оси. Считая, что эти источники находятся в максимумах распределения рис.16, координаты которых 
, 
и 
определяются из условия, когда аргумент функции 
равен нулю, к примеру, из 
следует 
, откуда 
. Но так как угол отклонения лучей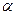 
, формирующих первый порядок дифракции на периодической структуре с периодом 
(у структуры с синусоидальным пропусканием имеются только два первых порядка 
) равен 
, то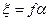 
, и искомые координаты определятся выражениями:
| (34) |
запишем уравнения этих сферических волн в плоскости изображения в приближении Френеля с амплитудами, выраженных в относительных единицах
| (35) |
Распределение освещенности в интерференционной картине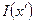 
будет иметь вид
 .
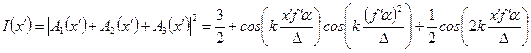| (36) |
График этого распределения показан на рис. 17. Первый член этого выражения представляет собой постоянную составляющую, второй член – изображение исходной периодической структуры. Действительно, период косинуса здесь определяется из соотношения
. (37)
Так как 
, то период будет
, (38)
что совпадает с геометрооптическим результатом, так как увеличение 
будет
. (30)
Наличие структуры с периодом 
(третий член) вызвано тем, что при расчете предмет (структура) находился в не в предметной плоскости, а в передней фокальной. При точном расчете эта структура исчезает.
Из изложенного следует, что изображение периодической структуры произойдет, если в фокальной плоскости образуется распределение типа приведенного на рис.17, т.е. у распределения будет два побочных максимума с координатами 
и . В принципе для этого достаточно, что хотя бы малая часть дифрагированных лучей прошла бы через оправу объектива микроскопа. При этом правда контраст изображения был бы невелик, так как уровень фона, который создается распределением с вершиной 
, был бы очень большим. Аббе предложил, что изображение удовлетворительного качества возникнет, если центральный дифрагированный луч пройдет через оправу объектива.
Из рис. 15 видно, что это наступит если 
. Так как предмет в микроскопе расположен вблизи фокальной плоскости объектива, то можно считать, что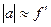 
. Учитывая, что 
получим величину минимально разрешимого объекта в микроскопе
 ,
| (40) |
где 
- т.н. числовая апертура. Если среда между объективом и предметом имеет показатель преломления 
, т.н. иммерсия. При этом разрешение микроскопа повышается т.к. выражение (40) примет вид (мокрый объектив)
 .
| (41) |
Полученное соотношение носит название критерий Аббе разрешающей способности микроскопа.
Отметим аналогию критериев Релея и Аббе. В случае освещения объекта в микроскопе параллельным пучком, в объектив попадает наклонный параллельный дифрагированный пучок, который можно считать как бы исходящего из точечного источника в бесконечности. Но именно такие пучки попадают в объектив телескопа и определение разрешающей способности этих двух систем оказываются полностью эквивалентны. Наличие в критерии Релея множителя 1,22 объясняется тем, что там изначально рассматривалась дифракция на круглой апертуре. В случае же микроскопа считалось, что дифракция происходит на щели, а точнее, в двумерном случае – на квадратном отверстии – что, конечно, неверно. Этот множитель появился как отношение первого корня функции Бесселя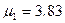 
(для круглого отверстия) и синуса (для квадратного отверстия) 
( 
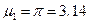). Но тем не менее эта неточность не существенна, поскольку оба критерия носят оценочный, относительный характер. Кстати, в некоторых публикациях формулу критерия Аббе записывают с таким множителем.
[1] Переменная отсутствует, поскольку предполагается, что она выражена через 
и 
в силу соотношения 
[2] Это справедливо лишь для участков интерференции вблизи оси, когда для сферической волны справедливо приближение Френеля.
[3] Для распределения Эри среднеквадратическая оценка не приемлема, так как интеграл, выражающий второй момент распределения, не является сходящимся.
[4] Частный случай этой теоремы рассматривался ранее в разделе интерференция, условия когерентности, опыт Юнга.
Дата добавления: 2018-10-27; просмотров: 948; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!