Основные алгоритмы обработки данных .

Цель работы:

Ознакомление с алгоритмами интерполирования табличных функций. Применение этих алгоритмов для построения аналитических выражений, представляющих таблицы экспериментальных данных, а также для замены трудновычислимых функций алгебраическими многочленами.

Порядок выполнения задания:

Ознакомиться с методами интерполирования табличных функций алгебраическими многочленами в форме Лагранжа и Ньютона [1]. Построить процедуры, реализующие эти методы средствами системы Maple.

В качестве модельного примера построения интерполяционного многочлена Лагранжа рассмотрим интерполирование табличных значений функции

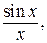вычисленных на равномерной сетке узлов В первой точке зададим явные значения функции, чтобы исключить неопределенность при делении на ноль. Вычисление произведений числителя и знаменателя в формуле Лагранжа (см. [1]) выполняем циклом с пропуском. Формулу для вычисления многочлена в точке программируем в виде функции.

Uses CRT;

const

n=4;h=2;

type

dann=array[0..n] of real;

var

X,Y:dann;

k: integer;

t,z: real;

function Lagrange(n:integer;X,Y:dann;t:real):real;

var

p,z: real;

k,j: integer;

begin

z:=0;

for k:=0 to n do

begin

p:=1;

for j:=0 to n do

begin

if k<>j then

p:=p*(t-X[j])/(X[k]-X[j]);

end;

z:=z+Y[k]*p;

end;

Lagrange:=z;

end;

begin

clrscr;

X[0]:=0;Y[0]:=1;

for k:=1 to n do

begin

X[k]:=k*h;

Y[k]:=sin(X[k])/X[k];

end;

for k:=0 to 2*n do

begin

t:=k*h/2;

z:=Lagrange(n,X,Y,t);

WRITELN(t:6:2,z:14:6);

End;

end.

Интерполяционный многочлен Ньютона.

Поскольку узлы интерполирования равноотстоящие, построим таблицу конечных разностей [1] и вычислим с ее помощью интерполяционный многочлен в форме Ньютона. Для удобства работы с индексами элементов двумерного массива будем использовать транспонированную таблицу разностей. В процедуре Newton предусмотрим возможность вычисления многочлена в точке не по всем, а по нескольким первым узлам, чтобы иметь возможность строить многочлены меньшей степени.

Uses CRT;

const

n=4;h=2;

type

dann=array[0..n] of real;

table=array[0..n+1] of dann;

var

X,Y:dann;

k: integer;

t,z: real;

dif:table;

pow:integer;

function Newton(n,p:integer;X,Y:dann;t:real):real;

var

q,z: real;

k,j: integer;

begin

dif[0]:=Y;

for k:=1 to n do

begin

for j:=0 to n-k do

dif[k][j]:=dif[k-1,j+1]-dif[k-1,j];

end;

z:=Y[0];

q:=1;

for k:=1 to p do

begin

q:=q*(t-X[k-1])/k/h;

z:=z+q*dif[k,0];

end;

Newton:=z;

end;

begin

clrscr;

X[0]:=0;Y[0]:=1;

for k:=1 to n do

begin

X[k]:=k*h;

Y[k]:=sin(X[k])/X[k];

end;

pow:=4;

for k:=0 to 2*n do

begin

t:=k*h/2;

z:=Newton(n,pow,X,Y,t);

WRITELN(t:6:2,z:14:6);

End;

end.

Практическая работа 6

Методы вычислений.

Реализация алгоритмов вычислительной математики на языках программирования в визуальной среде DELPHI. Метод наименьших квадратов. Гармонический анализ

Цель работы:

Изучение методов обработки экспериментальных данных

Ознакомиться с численными алгоритмами метода наименьших квадратов, с ортогональными на дискретной сетке узлов системами функций (тригонометрический базис). Реализовать алгоритмы построения тригонометрических полиномов для аппроксимации периодических на произвольном отрезке дискретных сигналов.

1. Применить учебную программу построения коэффициентов тригонометрического полинома для аппроксимации периодических сигналов, заданных на дискретных сетках периода [0..T]. Построить график полученного решения.

2. Построить графики спектральных характеристик сигнала, используя процедуры построения графиков предыдущей лабораторной работы.

Образец выполнения задания:

Пусть функция f ( t ) задана на равномерной сетке отрезка [x0,x0 + T] и продолжена периодическим образом на всю ось. Следовательно, ее можно представить в виде тригонометрического полинома (как частичной суммы ряда Фурье), приближенно представляющего функцию:

Коэффициенты полинома вычисляются по формулам:

где h = T / N , x_j = x ₀ + j h , y_j = f ( x_j ), ( j =1.. N ) – значения функции на равномерной сетке. Для учета периодичности наложим на функцию дополнительно условие y_N =( y ₀ + y_N )/2.

Установим на форму компоненты, как на рисунке

Назначим событию OnClick кнопки Button 1 операторы вычисления коэффициентов и опишем переменные и процедуры в разделе implementation как в приведенном ниже модуле (шрифт – жирный курсив). Сохраним проект в отдельной папке и отладив на конкретной функции f ( x )= x, заданной на отрезке [-p, p], применим эту программу для вычисления коэффициентов функций (по вариантам—индивидуально), затем используя предыдущую лабораторную работу, добавим к программе построение графика АЧХ, то есть величин коэффициентов в зависимости от их номеров.

unit trig;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, StdCtrls;

type

TForm1 = class(TForm)

Button1: TButton;

ListBox1: TListBox;

procedure Button1Click(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

implementation

{$R *.dfm}

const

N=50; { число узлов }

T=2*Pi; { период }

x0=-Pi;

h=T/N; { шаг сетки }

m=20;{ число коэффициентов }

Type

koeff=array[0..m] of real;

dann=array[0..N] of real;

Var

Y:dann;

a,b:koeff;

function f(t:real):real;

Begin

f:=t;

end;

procedure Trig(m,N:integer;Y:dann;var a,b:koeff);

Var

j,k:integer;

p,q:real;

x:real;

Begin

for k:=0 to m do

Begin

p:=0;q:=0;

for j:=1 to N do

Begin

x:=x0+j*h;

p:=p+Y[j]*cos(2*Pi*x*k/T);

q:=q+Y[j]*sin(2*Pi*x*k/T);

end;

a[k]:=p*2/N;

b[k]:=q*2/N;

end;

procedure TForm1.Button1Click(Sender: TObject);

Var

j:integer;

s1,s2,s3:string;

begin

for j:=0 to N do

Y[j]:=f(x0+j*h);

Y[N]:=(Y[0]+Y[N])/2;

Trig(m,N,Y,a,b);

for j:=0 to m do

Begin

str(j:2,s1);

str(a[j]:8:4,s2);

str(b[j]:8:4,s3);

listbox1.Items.Add(s1+s2+s3);

end ;

end;

end.

Практическая работа 7

Визуальное программирование

Цель работы:

Изучение технологии программирования сверху-вниз, интегрированное применение изученных методов обработки экспериментальных данных

Практическая работа выполняется самостоятельно на заключительном этапе изучения курса и ставит целью освоение и применение методов вычислительной математики и способов визуализации данных при решении учебных и профессиональных задач. Для выполнения работы требуется:

изучить основные алгоритмы вычислительной математики: решение уравнений (поиск корня уравнения), численное интегрирование, аппроксимация данных по методу наименьших квадратов, численное решение обыкновенных дифференциальных уравнений, методы гармонического анализа периодических функций;

освоить приемы работы в математических и инженерных (Maple, MathCAD) пакетах при обработке и визуализации данных и результатов вычислений.

Постановка задачи:

Рассматривается функция F ( t , t ), представляющая собой финитную функцию, определенную на конечном носителе длины t и продолженную периодически (период T > t) на всю ось. С помощью языка программирования, визуальной среды программирования и методов гармонического анализа вычислить коэффициенты Фурье аппроксимирующего тригонометрического полинома на дискретном множестве точек периода, построить графики исходного сигнала, тригонометрического полинома для различных степеней, а также график спектра амплитуд сигнала. Программные модули, реализующие самостоятельные алгоритмы, выполнить в виде процедур и функций. Написать программу на языке программирования Паскаль для решения своего варианта задачи (10 вариантов задания). Демонстрационный вариант программы подготовить в среде визуального программирования (Turbo Delphi). Построить блок-схемы задачи и вспомогательных частей алгоритма. Оформление графиков и таблиц выполнять средствами математического пакета Maple. Выполнить решение задачи средствами математических пакетов в аналитическом виде. Сравнить спектры амплитуд дискретного и аналогового сигналов.

Указания и пояснения.

Функция F ( t , t ) представляет собой периодический сигнал единичной амплитуды длительности t =1 (рис 2.1-2.10, в соответствии с номером варианта по последней цифре студенческого билета). Значение величины периода Т есть наименьший положительный корень полинома (таблица 1- по вариантам), который вычисляется любым из известных методов нахождения корня уравнения. Функция считается продолженной периодически на всю ось. На отрезке периода методами численного интегрирования (метод прямоугольников, метод трапеций) вычисляются коэффициенты тригонометрического полинома Фурье, аппроксимирующего функцию. Строятся графики исходного сигнала и приближающих его полиномов нескольких степеней. Далее строится график амплитудного спектра дискретного сигнала.

Затем задача решается средствами математического пакета Maple, позволяющего выполнить вычисления как для аналогового (в аналитическом виде), так и для дискретного сигнала (дискретное преобразование Фурье в комплексной форме). Спектры амплитуд дискретного и аналогового сигналов выводятся на совместном графике и сравниваются их свойства.

Таблица 1. Варианты полиномов

№ варианта	Полином
1	x^5-8*x-1
2	x^5-3*x-3
3	2*x^4-x^3-8
4	x^6-4*x^4-2
5	x^6-4*x^4-3
6	x^6-3*x^3-2
7	x^5-7*x-14
8	x^5-x^3-1
9	x^5-2*x^3-4
10	x^6-3*x^4-5

Порядок выполнения задания.

Построить проект в среде Turbo DELPHI, решающий поставленную задачу по технологии сверху-вниз. Отладить взаимодействие компонент на форме. На основе выполненных ранее практических работ наполнить работу командных кнопок методами, решающими поставленную задачу.

Практическая работа 8

Дата добавления: 2018-10-27; просмотров: 322; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 Следующая ⇒

Мы поможем в написании ваших работ!