ПРЯМОЙ, ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ

Представление чисел в эвм

ФОРМЫ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ В ЭВМ

Любая информация (числа, команды, алфавитно-цифровые записи и т. п.) представляется в ЭВМ в виде двоичных кодов (двоичных слов) фиксированной или переменной длины. Отдельные элементы двоично­го кода, имеющие значение 0 или 1, называют разрядами или битами. В ЭВМ слова часто разбивают на части, называемые слогами или байтами. В современных ЭВМ широко используется байт, содержащий  8 бит (разрядов).

Двоичный разряд представляется в ЭВМ некоторым техническим устройством, например триггером, двум различным состояниям кото­рого приписывают значения 0 и 1. Набор соответствующего количе­ства таких устройств служит для представления многоразрядного двоичного числа (слова).

В ЭВМ применяют две формы представления чисел: с фиксиро­ванной запятой (точкой) и с плавающей запятой (точкой). Эти формы называют также соответственно естественной и полулогарифмической.

При представлении чисел с фиксированной запятой положение за­пятой фиксируется в определенном месте относительно разрядов чис­ла. Обычно подразумевается, что запятая находится или перед старшим разрядом, или после младшего. В первом случае могут быть представлены только числа, которые по модулю меньше 1, во вто­ром — только целые числа.

 

 

Рис. 1.1. Форматы данных для представления двоичных чисел с фиксированной запятой (точкой):

На рис. 1.1 показаны примеры форматов данных для представле­ния двоичных чисел с фиксированной запятой и соответствующие раз­рядные сетки. По сложившейся в вычислительной технике традиции нумерация разрядов (бит) в разрядной сетке в машинах общего назна­чения (ЕС ЭВМ) ведется слева направо, а в малых ЭВМ, микро-ЭВМ и микропроцессорах — справа налево. На разрядной сетке указаны веса разрядов.

При представлении числа со знаком для кода знака выделяется «знаковый» разряд (обычно крайний слева). В этом разряде 0 соответ­ствует плюсу, а 1 — минусу.

На рис. 1.1, a показан формат для чисел с запятой, фиксированной перед старшим разрядом. В этом формате могут быть с точностью до 2^–(n-1) представлены числа (правильные дроби) в диапазоне

2^–(n-1) £ |x| £ 1 - 2^–(n-1)

Первые ЭВМ были машинами с фиксированной запятой, причем запятая фиксировалась перед старшим разрядом числа. В настоящее время, как правило, форму с фиксированной запятой применяют для представления целых чисел (запятая фиксирована после младшего разряда).

Используют два варианта представления целых чисел: со знаком и без знака. В последнем случае все разряды разрядной сетки служат для представления модуля числа.

Представление чисел с фиксированной запятой используется как основное и единственное лишь в сравнительно небольших по своим вычислительным возможностям машинах, применяемых в системах передачи данных, для управления технологическими процессами и обработки измерительной информации в реальном масштабе вре­мени.

В машинах, предназначенных для решения широкого круга вычис­лительных задач, основным является представление чисел с плаваю­щей запятой, не требующее масштабирования данных. Однако в таких машинах часто наряду с этой формой представления чисел используется также и представление с фиксированной запятой для целых чисел, поскольку операции с такими числами выполняются за меньшее вре­мя. В частности, к операциям с целыми числами сводятся операции над кодами адресов (операции индексной арифметики).

Представление числа с плавающей запятой в общем случае имеет вид

     x = s^pq; |q| < 1,        (2.3)

где q — мантисса числа х , s^p — характеристика числа х ; р - порядок-, s — основание характеристики (обычно целая степень числа 2).

Мантисса (правильная дробь со знаком) и порядок (целое число со знаком) представляются в системе счисления с основанием, рав­ным s (в соответствующей двоично-кодированной форме). Знак числа совпадает со знаком мантиссы.

Порядок р, который может быть положительным или отрицатель­ным целым числом, определяет положение запятой в числе х .

На рис. 1.2 показаны примеры форматов данных для чисел с пла­вающей запятой. Одна часть бит формата используется для пред­ставления порядка, а другая — для мантиссы.

Арифметические дей­ствия над числами с плавающей запятой требуют выполнения помимо операций над мантиссами определенных операций над порядками (сравнение, вычитание и др.). Для упрощения операций над поряд­ками их сводят к действиям над целыми положительными числами (целыми числами без знаков), применяя представление чисел с пла­вающей запятой со «смещенным порядком».

В случае представления числа с плавающей запятой со смещен­ным порядком к его порядку р прибавляется целое число - смеще­ние N = 2', где k — число двоичных разрядов, используемых для модуля порядка.

Смещенный порядок р_см =р+N всегда положителен. Для его представления необходимо такое же число разрядов, как и для модуля и знака порядка р.

Важная особенность смещенных порядков состоит в том, что если для порядков р ' и р ", представляющих собой целые числа со зна­ками, выполняется соотношение

p' ³ p",

 то и для положительных целых чисел соответствующих смещенных порядков р '_см и р "_см всегда

р '_см ³ р "_{см .} Это представление числа называют также полулогарифмиче­ским, так как часть числа - характеристика - выражена в логариф­мической форме.

 

Рис. 1.2. Представление в ЭВМ чисел с плавающей запятой:

 

При фиксированном числе разрядов мантиссы любая величина представляется в машине с наибольшей возможной точностью норма­лизованным числом.

Число х = s"q называется нормализованным, если мантисса q удо­влетворяет условию

1 > |q| ³ 1/s,                           (2.4)

т. е. старший разряд мантиссы в s-ричной системе отличен от нуля. В процессе вычислений может получаться ненормализованное число. В этом случае машина, если это предписано командой, авто­матически нормализует его («нормализация результата» операции).

Пусть r старших разрядов s-ричной мантиссы равны 0. Тогда нормализация заключается в сдвиге мантиссы на r разрядов влево и уменьшении порядка на r единиц, при этом в младшие r раз­рядов мантиссы записывается 0. После такой операции число не ме­няется, а условие (2.4) выполняется. При нулевой мантиссе нормали­зация невозможна.

В различных ЭВМ применяются представления чисел с плаваю­щей запятой в системах счисления с различными основаниями, но равными целой степени числа 2 (s = 2^w), при этом порядок р пред­ставляется целым числом, а мантисса q — числом, в котором группы по w двоичных разрядов изображают цифры мантиссы с основанием системы счисления s= 2^w.

Примерами применяемых форм чисел с плавающей запятой с раз­личными основаниями системы счисления являются

x=2^pq (1 > |q|³1/2);

x=8^pq (I > |q| ³ 1/8);

x = l6^pq (I > |q| ³ 1/16).

В скобках указаны соответствующие условия получения нормали­зованных чисел.

Использование для чисел с плавающей запятой недвоичного осно­вания несколько уменьшает точность вычислений (при заданном числе разрядов мантиссы), но позволяет увеличить диапазон представляемых в машине чисел и ускорить выполнение некоторых операций, в частно­сти нормализации, за счет того, что сдвиг может производиться сразу на несколько двоичных разрядов (на четыре разряда для s = 16). Кроме того, уменьшается вероятность появления ненормализованных чисел в ходе вычислений.

Диапазон представимых в машине чисел с плавающей запятой за­висит от основания системы счисления и числа разрядов, выделенных для изображения порядка. Точность вычислений при плавающей за­пятой определяется числом разрядов мантиссы. С увеличением числа разрядов мантиссы увеличивается точность вычислений, но увеличи­вается и время выполнения арифметических операций.

Задачи, решаемые на ЭВМ, предъявляют различные требования к точности вычислений. Поэтому во многих машинах используется не­сколько форматов с плавающей запятой с различным числом разря­дов мантиссы.

ПРЯМОЙ, ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ

В ЭВМ с целью упрощения арифметических операций применяют специальные коды для представления чисел. При помощи этих кодов упрощается определение знака результата операции, операция вычита­ния (или алгебраического сложения) чисел сводится к арифметическому сложению их кодов, облегчается выработка признаков переполне­ния разрядной сетки. В результате упрощаются устройства ЭВМ, выполняющие арифметические операции.

Для представления отрицательных чисел в ЭВМ применяют пря­мой, обратный и дополнительный коды. Положительные числа пред­ставляются в прямом коде. Во всех этих кодах выделяются цифровые разряды и знаковый (крайний слева), представляющий знак числа, при­чем знак плюс кодируется цифрой 0, а знак минус цифрой 1.

Прямой код двоичного числа G с (n-1) цифровыми разрядами определяется как

G_пр = 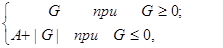(1.5)

где А — величина, равная весу знакового разряда. Для дробных чисел А = 1, а для целых А = 2^n-1.

Сложение в прямом коде чисел, имеющих одинаковые знаки, вы­полняется достаточно просто. Числа складываются, и сумме присваи­вается код знака слагаемых. Значительно более сложной является опе­рация алгебраического сложения в прямом коде чисел с различными знаками. В этом случае приходится определять большое по модулю число, производить вычитание чисел и присваивать разности знак большего по модулю числа.

Операция вычитания (алгебраического сложения) сводится к опе­рации простого арифметического сложения при помощи обратного и дополнительного кодов, используемых для представления отрица­тельных чисел в машине.

Чтобы представить двоичное отрицательное число в обратном ко­де, нужно поставить в знаковый разряд 1, а во всех других разрядах заменить 1 нулями, а нули единицами.

Обратный код, если рассматривать его как число, является допол­нением модуля исходного числа до наибольшего числа без знака, по­мещающегося в разрядную сетку. Для n-разрядной сетки имеем

Go6p=2-2 ^–(n-1) – lG^-l,             (1.6)

если G^- — двоичная дробь, и

G^-_обр = 2ⁿ – 1 - |G^-|                   (1.6a)

если G^- — целое двоичное число.

При представлении отрицательного двоичного числа в дополни­тельном коде ставят 1 в разряд знака, а цифровую часть числа заме­няют дополнением модуля числа до 1 или 2^n-1 соответственно для дробей и целых чисел. Дополнительный код отрицательного числа G определяется выражением

G^- _доп=2-|G^-| (1.7)

если G^- — двоичная дробь, и

 G^- _доп=2ⁿ-|G^-| (1.7a)

 

если G^- — целое двоичное число.

Обратный и дополнительный коды числа можно рассматривать как двоичные числа без знаков, при этом для двоичных дробей G^-_доп = G^-_обр + 2^-(n-1), а для двоичных целых чисел С^-_доп=С^-_обр+1.

Таким образом, дополнительный код числа может быть получен из обратного путем прибавления 1 к младшему разряду обратного кода.

При выполнении расчетов на машине могут возникнуть как «по­ложительный», так и «отрицательный» 0. Положительный 0 в прямом коде имеет вид

(+0)_пр= 000... 0.

Отрицательный 0 изображается в прямом коде

( - 0)_пр= 100. ..О,

в обратном

(-0)_обр= 111...1;

в дополнительном коде отрицательный 0 отсутствует.

При представлении положительных чисел прямым кодом, а отри­цательных дополнительным нуль имеет единственное изображение. При применении обратного кода «положительный» и «отрица­тельный» 0 имеют разные изображения.

Изменению знака отрицательного числа соответствует инвертиро­вание его кода, если число представлено в обратном коде, и инверти­рование и добавление 1 младшего разряда, если отрицательное число представлено в дополнительном коде. В результате получается прямой код соответствующего положительного числа. Сказанное следует из соотношений:

для дробей

-G^-_пр = |G^-| = 2 – 2^-(n-1) – G^-_обр                (1.8)

-G^-_пр = |G^-| = 2 – G^-_доп                      (1.9)

 

для целых чисел

. -G^-_пр = |G^-| = 2ⁿ – 1 – G^-_обр                         (1.8a)

 -G^-_пр = |G^-| = 2ⁿ – G^-_доп                (1.9a)

Рассмотрим применение обратного и дополнительного кодов при алгебраическом сложении n-разрядных двоичных чисел G и Q, когда одно из них или оба числа отрицательны. Могут быть сформулиро­ваны следующие правила (предполагаем, что модуль алгебраической суммы меньше 1 для дробей и меньше 2^n-1 для целых чисел, и, следо­вательно, код суммы представим в n-разрядной сетке).

При алгебраическом сложении двух двоичных чисел с использова­нием обратного (или дополнительного) кода положительные сла­гаемые представляются в прямом коде, а отрицательные - в обратном (дополнительном) и производится арифметическое суммирование этих кодов, включая разряды знаков, .которые при этом рассматриваются как старшие разряды. При возникновении переноса из разряда знака единица переноса прибавляется к младшему разряду суммы кодов  при использовании обратного кода и отбрасывается при использова­нии дополнительного кода. В результате получается алгебраическая сумма в прямом коде, если эта сумма положительна, и в обратном (дополнительном), если она отрицательна.

Признак переполнения разрядной сетки. При алгебраическом сло­жении двух чисел, помещающихся в разрядную сетку, может возник­нуть переполнение, т. е. образоваться сумма, требующая для своего представления на один цифровой разряд больше по сравнению с раз­рядной сеткой слагаемых. Можно сформулировать следующее правило (признак) для обнаружения переполнения разрядной сетки.

При алгебраическом сложении двух двоичных чисел с использова­нием прямого кода для представления положительных и дополнитель­ного (обратного) кода для представления отрицательных чисел призна­ком переполнения является наличие переноса в знаковый разряд суммы при отсутствии переноса из ее знакового разряда (положитель­ное переполнение) или наличие переноса из знакового разряда суммы при отсутствии переноса в ее знаковый разряд (отрицательное пере­полнение). Если и в знаковый, и из знакового разряда суммы есть переносы или нет этих переносов, то переполнение отсутствует. При положительном переполнении результат операции положительный, а при отрицательном отрицательный.

 

---

Дата добавления: 2018-10-27; просмотров: 267; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!