Неинерциальные системы отсчета.
Лекция 4.
3. Закон сохранения импульса. Неинерциальные системы отсчета. 32
Закон сохранения импульса.
3.1.1. Основные понятия. ________________________ 32
3.1.2. Вывод и формулировка закона сохранения импульса. 32
3.1.3. Закон движения центра масс. _______________ 34
3.1.4. Уравнение движения тела переменной массы. Реактивное движение. 35
3.2. Неинерциальные системы отсчета. _________________ 36
3.2.1. Второй закон Ньютона в неинерциальных системах отсчета. 37
3.2.2. Переносная сила инерции.__________________ 38
3.2.3. Сила инерции Кориолиса.__________________ 39
3.2.3.1. Кориолисово ускорение.__________________ 39
3.2.3.2. Примеры проявления сил Кориолиса._______ 41
3.2.4. Центробежная сила инерции.________________ 43
Вопросы для самоконтроля._____________________ 44
Задачи для самостоятельного решения____________ 44
Литература____________________________________ 44
3.1. Закон сохранения импульса.
3.1.1. Основные понятия.
Механической системой называется совокупность материальных точек (тел), рассматриваемых как единое целое.
Внутренними силами называются силы взаимодействия между материальными точками (телами) механической системы.
Внешними силами называются силы, с которыми на материальные точки (тела) системы действуют внешние тела.
Замкнутой системой называется механическая система, на которую не действуют внешние силы.
3.1.2. Вывод и формулировка закона сохранения импульса.
Рассмотрим механическую систему из N тел, массы и скорости которых соответственно равны m 1 , m 2 , m 3 ,…, mn; и 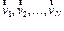 .
.
|
|
|
Запишем второй закон Ньютона для каждого из N тел механической системы:
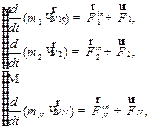
| (3.1) |
где: 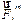 - равнодействующая внутренних сил, приложенных к i-тому телу системы;
- равнодействующая внутренних сил, приложенных к i-тому телу системы; 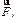 - равнодействующая внешних сил, приложенных к i-тому телу системы.
- равнодействующая внешних сил, приложенных к i-тому телу системы.
Проведем сложение уравнений (3.1):
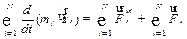
| (3.2) |
В левой части полученного выражения имеем:
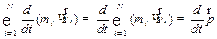
| (3.3) |
где: 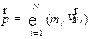 представляет собой суммарный импульс всех тел системы, т.е. импульс системы.
представляет собой суммарный импульс всех тел системы, т.е. импульс системы.
Первый член в правой части выражения (3.2) представляет собой геометрическую сумму всех внутренних сил, приложенных ко всем телам системы. По третьему закону Ньютона каждой внутренней силе 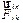 соответствует равная ей по модулю и противоположная по направлению сил
соответствует равная ей по модулю и противоположная по направлению сил 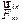 , поэтому:
, поэтому:
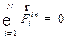
| (3.4) |
Выражение (3.2) преобразуется к виду:
| ЗАКОН | 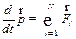
| (3.5) |
| “ Производная от импульса системы по времени равна сумме внешних сил, действующих на систему ”.- Закон изменения импульса системы тел.
| ||
Если векторная сумма внешних сил равна нулю, или внешние силы отсутствуют, то:
| ЗАКОН! | 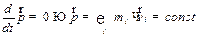
| (3.6) | |
|
импульс системы тел сохраняется! “ Импульс замкнутой системы есть постоянная величина” .
Закон сохранения импульса (количества движения) - фундаментальный, универсальный закон природы.
| |||
Закон сохранения импульса носит уникальный характер, т.к. он справедлив и выполняется для замкнутых систем микрочастиц, т.е. он является фундаментальным (основополагающим) законом природы.
Закон сохранения импульса является следствием определенного свойства симметрии пространства – его однородности.
Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы тел как целого, её физические свойства и законы движения не изменяются, иными словами, не зависят от выбора положения начала координат инерциальной системы отсчета.
3.1.3. Закон движения центра масс.
Центром масс системы (тела) называется воображаемая точка C, расположение определяется радиус-вектором:
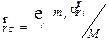 , , 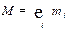
| (3.7) |
где: mi и 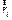 - соответственно масса и радиус-вектор i-той материальной точки;
- соответственно масса и радиус-вектор i-той материальной точки; 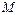 - масса системы.
- масса системы.
Для скорости центра масс получаем:
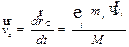 или или 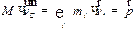
| (3.8) |
Импульс системы материальных точек равен произведению суммарной массы системы на скорость ее центра масс.
Откуда получаем закон движения центра масс системы материальных точек (тела, тел):
|
|
|
| ЗАКОН! | 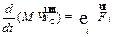
| (3.9) |
| “ Центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная векторной сумме всех внешних сил, приложенной системе”. | ||
Из закона сохранения импульса вытекает, что центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным.
3.1.4. Уравнение движения тела переменной массы. Реактивное движение.
Движение некоторых тел сопровождается изменением их массы. Выведем уравнение движения тела переменной массы на примере движения ракеты. Если в момент времени t масса ракеты m, а ее скорость 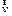 , то по истечении времени dt ее масса уменьшится на dm и станет равной m –dm, а скорость станет равной
, то по истечении времени dt ее масса уменьшится на dm и станет равной m –dm, а скорость станет равной 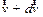 . Тогда изменение импульса системы за отрезов времени dt будет равным:
. Тогда изменение импульса системы за отрезов времени dt будет равным:
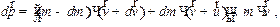
| (3.10) |
где 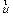 – скорость истечения газов относительно ракеты. Тогда импульс
– скорость истечения газов относительно ракеты. Тогда импульс
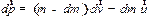
| (3.11) |
Если учесть, что 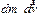 бесконечно малая величина относительно других, то согласно закону (3.5) изменения импульса системы тел получим:
бесконечно малая величина относительно других, то согласно закону (3.5) изменения импульса системы тел получим:
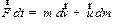
| (3.12) |
или
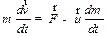
| (3.13) |
Величину 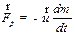 называют реактивной силой.
называют реактивной силой.
Если 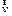 и
и 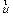 противоположны по направлению, то ракета ускоряется, если
противоположны по направлению, то ракета ускоряется, если 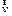 и
и 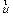 совпадают по направлению, то ракета тормозится.
совпадают по направлению, то ракета тормозится.
|
|
|
Таким образом:
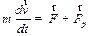
| (3.14) |
Это уравнение движения тела переменной массы. Его вывел И.В. Мещерский (1859 – 1935).
Идея применения реактивной силы для создания летательных аппаратов высказывалась ещё в 1881 году Н.И. Кибальчичем (1857 – 1905). В 1903 году он опубликовал статьи по теории жидкой основы реактивного двигателя.
Если на ракету не действуют никакие внешние силы и, считая, что скорость выбрасываемых газов относительно ракеты постоянна, ракета движется прямолинейно, получим следующее:
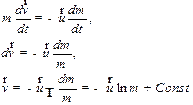
| (3.15) |
Значение постоянной интегрирования c определим из начальных условий.
Если в начальный момент времени v0 =0, а её стартовая масса равна m0, то Const = u×ln m0, следовательно,
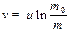
| (3.16) |
Последнее соотношение – формула Циалковского. Она показывает, что:
1) чем больше конечная масса ракеты m, тем больше должна быть стартовая масса ракеты m0;
2) чем больше u (скорость истечения газов), тем больше может быть конечная масса при данной стартовой массе ракеты.
Уравнение движущегося тела переменной массы и формула Циалковского получены для нерелятевистских движений, т.е. когда 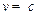 скорость ракеты много меньше скорости света в вакууме.
скорость ракеты много меньше скорости света в вакууме.
Неинерциальные системы отсчета.
Первый закон Ньютона утверждает, что состояния покоя и равномерного прямолинейного движения принципиально неразличимы. Другими словами, - это значит, что законы динамики имеют один и тот же вид в различных инерциальных системах отсчета, т.е. скорость движения системы отсчета не влияет на форму записи законов динамики. Физические утверждения или величины, вид или значения которых не зависят от перехода от одной инерциальной системы отсчета к другой называются инвариантами. В этом смысле можно говорить, что законы Ньютона инвариантны при переходе от одной инерциальной системы отсчета к другой.
Однако ньютоновская механика в неявном виде содержит более сильное утверждение. По определению силы ее мерой может служить деформация тел. Согласно аксиомам о независимости от выбора системы отсчета пространственных и временных промежутков это фактически предполагает, что силы остаются инвариантными даже в системах, движущихся с ускорением, т.е. в неинерциальных системах. То же самое можно сказать о массе.
Если силы и масса являются инвариантами в механике Ньютона, то величина ускорения может быть различной в разных неинерциальных системах (см. п. 1.4). Пусть имеются две системы отсчета 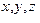 и
и 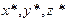 , одна из которых (см. рис. 11 и 12)
, одна из которых (см. рис. 11 и 12) 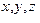 - покоится, а другая -
- покоится, а другая - 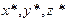 -движется с некоторым ускорением, т.е. является неинерциальной. В силу установленной инвариантности массы и сил в этих системах имеем:
-движется с некоторым ускорением, т.е. является неинерциальной. В силу установленной инвариантности массы и сил в этих системах имеем:
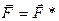 и и 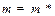
| (3.17) |
Если ускорение тела в системе отсчета 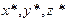 -
- 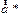 , а сама система движется относительно неподвижной системы с ускорением
, а сама система движется относительно неподвижной системы с ускорением 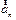 , которое называют переносным ускорением, то общее ускорение тела относительно системы
, которое называют переносным ускорением, то общее ускорение тела относительно системы 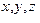 складывается из этих ускорений и еще двух составляющих. Ранее в разделе 1.4.1 было получено (1.37):
складывается из этих ускорений и еще двух составляющих. Ранее в разделе 1.4.1 было получено (1.37):
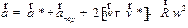 , ,
|
Следовательно, второй закон Ньютона, записанный в таком же виде как и для инерциальных систем отсчета, т.е. в виде
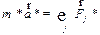 не выполняется. не выполняется.
|
3. 2. 1. Второй закон Ньютона в неинерциальных системах отсчета.
Для решения основной задачи динамики в неинерциальных системах отсчета необходимо получить основное уравнение динамики (Второй закон Ньютона в неинерциальных системах отсчета).
Основное уравнение динамики в неподвижной системе отсчета записывается следующим образом:
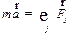 , ,
| (3.18) |
или
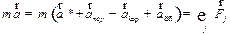 , ,
| (3.19) |
где 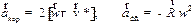 .
.
Как уже установлено, величина сил и масс являются инвариантами в механике Ньютона. Согласно (3.17) имеем 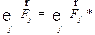 и
и 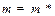 . Тогда (3.19) запишем так
. Тогда (3.19) запишем так
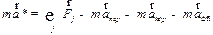
| (3.20) |
или
| ЗАКОН! | 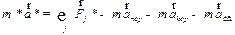
| (3.21) |
| Сравнивая уравнения (3.18) и (3.21), можно заметить, что второй закон Ньютона сохранит свой смысл в неинерциальных системах отсчета, если члены ( | ||
Такие «силы» (отметим, что для них всегда невыполним третий закон Ньютона, т.к. эти «силы» вызваны не взаимодействиями между телами, а ускорением системы отсчета) получили название сил инерции ( 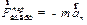 ,
, 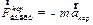 и
и 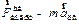 ). Первая из сил, стоящих в скобках представляет собой так называемую переносную силу инерции, вторая - силу инерции Кориолиса, а третья – центробежную силу инерции.
). Первая из сил, стоящих в скобках представляет собой так называемую переносную силу инерции, вторая - силу инерции Кориолиса, а третья – центробежную силу инерции.
Далее на примерах выясним проявление этих «сил».
3. 2. 2. Переносная сила инерции.
Переносные силы инерции есть силы инерции при ускоренном поступательном движении системы отсчета.
| |||
| Рисунок 3.1 |
Пусть на тележке (см. рис. 3.1) к штативу подвешен шарик массой m. Пока тележка покоится или движется равномерно и прямолинейно, нить занимает вертикальное положение, и сила тяжести уравновешена силой натяжения нити. Если тележке придать ускорение 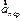 , то нить начнет отклоняться от вертикального положения на угол a пока результирующая сила
, то нить начнет отклоняться от вертикального положения на угол a пока результирующая сила
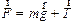
| (3.22) |
не обеспечит ускорение шарика равное 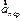 . Таким образом,
. Таким образом,
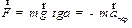
| (3.23) |
и
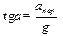
| (3.24) |
т.е. угол отклонения тем больше, чем больше ускорение тележки.
Относительно системы отсчета, связанной с ускоренно движущейся тележкой, шарик покоится, что возможно, если сила F уравновешена силой инерции, т.е.
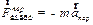
| (3.25) |
Примером проявления переносной силы инерции может служить поведение пассажиров в переполненном автобусе при его резком торможении, когда какая-то «непонятная сила» заставляет всех их дружно «валится» вперед по ходу движения.
3. 2. 3. Сила инерции Кориолиса.
Сила Кориолиса действует на тела, движущиеся относительно вращающейся системы отсчета.
3. 2. 3. 1. Кориолисово ускорение.
Для пояснения происхождения слагаемого 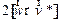 в формуле (1.37) рассмотрим так называемый «движущийся тротуар» - систему параллельных движущихся с различной скоростью дорожек (Такой тротуар был построен в Мельбурне во время подготовки к Олимпиаде). Если тело движется перпендикулярно дорожкам (см рис. 3.2)., то при переходе с одной дорожки на другую его скорость будет изменяться. Быстрота изменения скорости определяется двумя факторами: величиной различия скоростей двух соседних дорожек и быстротой перехода тела с одной дорожки на другую, т.е.
в формуле (1.37) рассмотрим так называемый «движущийся тротуар» - систему параллельных движущихся с различной скоростью дорожек (Такой тротуар был построен в Мельбурне во время подготовки к Олимпиаде). Если тело движется перпендикулярно дорожкам (см рис. 3.2)., то при переходе с одной дорожки на другую его скорость будет изменяться. Быстрота изменения скорости определяется двумя факторами: величиной различия скоростей двух соседних дорожек и быстротой перехода тела с одной дорожки на другую, т.е.
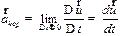 . .
| (3.26) |
Очевидно, что это ускорение должно зависеть как от разности скоростей
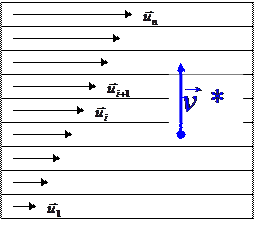
| и ширины соседних дорожек, так и скорости пересекающего их тела. Это ускорение называется кориолисовым или поворотным. Направление этого ускорения определяется направлением изменения скорости дорожек
На рис.18 |
| Рисунок 3.2 |
Известно, что этот вид ускорения проявляется во вращающихся системах координат. Величину кориолисова ускорения во вращающейся системе координат можно определить из следующего рассмотрения (см. рис. 3.3). В нем тело участвует в двух движениях: вращательном с угловой скоростью 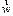 и равномерном прямолинейном со скоростью
и равномерном прямолинейном со скоростью 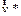 , направленной по радиусу вращения. Пусть за малый промежуток времени Dt тело сместится вдоль радиуса на расстояние DR = Ri +1 - Ri и при этом повернется на угол Dj = wDt. Общее изменение скорости состоит из двух слагаемых, одно из которых связано с увеличением тангенциальной скорости вращательного движения при переходе от меньшего радиуса Ri к большему Ri +1, т.е.
, направленной по радиусу вращения. Пусть за малый промежуток времени Dt тело сместится вдоль радиуса на расстояние DR = Ri +1 - Ri и при этом повернется на угол Dj = wDt. Общее изменение скорости состоит из двух слагаемых, одно из которых связано с увеличением тангенциальной скорости вращательного движения при переходе от меньшего радиуса Ri к большему Ri +1, т.е.
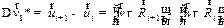 . .
| (3.27) | |
|
| ||
| Рисунок 3.3 | ||
Второе слагаемое 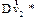 , изображенное на рис , обусловлено поворотом вектора
, изображенное на рис , обусловлено поворотом вектора 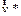 при переходе из начального(Ri) положения в конечное (Ri +1):
при переходе из начального(Ri) положения в конечное (Ri +1):
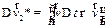 . .
| (3.28) |
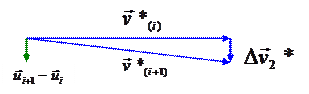
| Из рис. видно, что при стремлении Dt к нулю направления слагаемых
|
| Рисунок 3. 4 |
 Поэтому при
Поэтому при 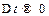 получаем формулу для поворотного ускорения:
получаем формулу для поворотного ускорения: 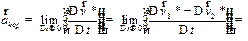
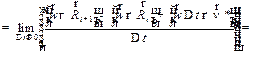
. 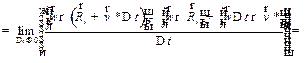
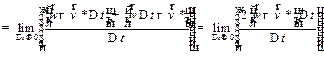
|
или окончательно приходим к результату
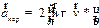 . .
| (3.29) |
3. 2. 3. 2. Примеры проявления сил Кориолиса.
Пусть шарик массой m движется с постоянной скоростью 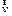 вдоль радиуса равномерно вращающегося диска, при этом
вдоль радиуса равномерно вращающегося диска, при этом 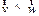 (см. рис. 3.5).
(см. рис. 3.5).
| а) | 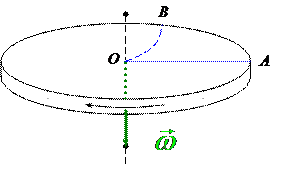
|
| б) | 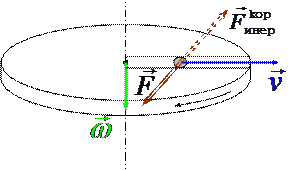
|
| Рисунок 3.5 | |
Если диск не вращается, то шарик, направленный вдоль радиуса, попадает в точку A. Если диск привести во вращение в направлении указанном стрелкой, то шарик будет катиться по кривой OB. Его скорость 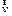 ¢ относительно диска меняет свое направление под действием некоторой силы, перпендикулярной скорости. Чтобы заставить шарик катиться по радиусу, используем жестко укрепленную на диске трубу, в которой шарик движется равномерно и прямолинейно со скоростью
¢ относительно диска меняет свое направление под действием некоторой силы, перпендикулярной скорости. Чтобы заставить шарик катиться по радиусу, используем жестко укрепленную на диске трубу, в которой шарик движется равномерно и прямолинейно со скоростью 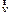 . При отклонении шарика стержень действует на него с некоторой силой
. При отклонении шарика стержень действует на него с некоторой силой 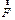 . Относительно диска шарик движется равномерно и прямолинейно, что можно объяснить тем, что сила
. Относительно диска шарик движется равномерно и прямолинейно, что можно объяснить тем, что сила 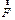 уравновешивается силой
уравновешивается силой  , - силой инерции, перпендикулярной скорости, которая и называется Кориолисовой силой.
, - силой инерции, перпендикулярной скорости, которая и называется Кориолисовой силой.
Сила инерции Кориолиса объясняет такие явления как отклонение Гольфстрима к северо-востоку, направление пассатов, дующих из области высокого давления в сторону экватора, рельеф берегов рек, текущих в меридианальном направлении, отклонение снарядов, выпущенных из огнестрельного оружия и т.п.
3. 2. 4. Центробежная сила инерции.
Центробежная сила инерции, действующая на тела во вращающихся системах отсчета в направлении радиуса от оси вращения, зависит от угловой скорости вращения системы отсчета и радиуса R, но не зависит от скорости тел относительно вращающейся системы отсчета.
Рассмотрим проявление центробежной силы инерции на следующем примере.
Пусть диск равномерно вращается с угловой скоростью w вокруг оси, проходящей через его центр. Пусть на диске на разных расстояниях друг от друга установлены маятники (см. рис.3.6).
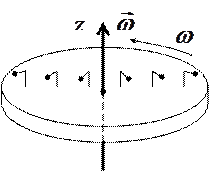
| 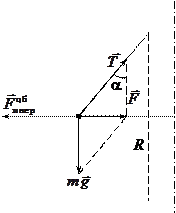
|
| Рисунок 3.6 | Рисунок 3.7 |
В инерциальной системе отсчета, связанной с комнатой, где установлен диск, выбранный шарик равномерно вращается по окружности радиусом R относительно оси проходящей через центр диска. Следовательно, на него действует главный вектор сил, вызывающий центростремительное ускорение:
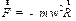
| (3.30) |
Относительно системы отсчета, связанной с диском шарик покоится (см. рис. 3.7), т.к. главный вектор сил 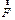 уравновешивается противоположно направленной центробежной силой
уравновешивается противоположно направленной центробежной силой 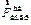 инерции, которая направлена от оси вращения диска и равна
инерции, которая направлена от оси вращения диска и равна
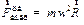
| (3.31) |
Главный вектор сил 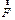 является равнодействующей силы тяжести и силы напряжения нити.
является равнодействующей силы тяжести и силы напряжения нити.
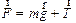
| (3.32) |
Когда движение шарика установится
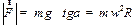
| (3.33) |
Следовательно, углы отклонения нитей маятников будут тем больше, чем больше радиус R и угловая скорость w, т.к.
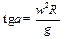
| (3.34) |
Вопросы для самоконтроля.
1. Что изучается в разделе "Динамика"?
2. Сформулируйте первый закон Ньютона.
3. Какие системы отсчета называются инерциальными?
4. Что такое инертность тел? Что такое масса? Единицы измерения массы. Как измеряется масса?
5. Что такое сила и как она измеряется? Единицы измерения силы.
6. Второй закон Ньютона. Импульс.
7. В чем заключается принцип независимости действия сил?
8. Сформулируйте третий закон Ньютона.
9. Есть ли границы применимости механики Ньютона?
Задачи для самостоятельного решения
2.9; 2.12; 2.16; 2.25; 2.30 [3] или 2.6; 2.13; 2.53; 2.52; 2.2 [4].
Литература
1. Савельев И.В. Курс общей физики, т.1.-М.:"Наука",-1977.-416с. (§5)
2. Трофимова Т.И. Курс физики.-М.:"Высш.шк.",-1985.-432с. (§4)
3. Волькенштейн В.С. Сб. задач по общему курсу физики.-М.: "Наука",-1985.-382 с.
4. Чертов А.Г., Воробьёв А.А. Задачник по физике.-М.: "Высш.шк.",-1981.-496с.
Дата добавления: 2018-10-27; просмотров: 644; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

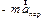 ), (
), ( 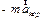 ) и (
) и ( 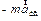 ) трактовать как некоторые дополнительные силы, возникающие в неинерциальной системе отсчета.
) трактовать как некоторые дополнительные силы, возникающие в неинерциальной системе отсчета. 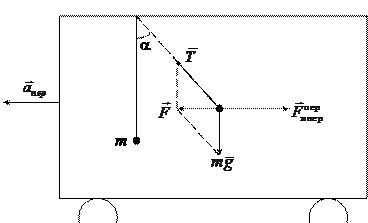
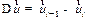 .
.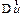 направлено вправо по отношению к вектору скорости
направлено вправо по отношению к вектору скорости 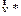 тела, т.е. перпендикулярно ему.
тела, т.е. перпендикулярно ему. 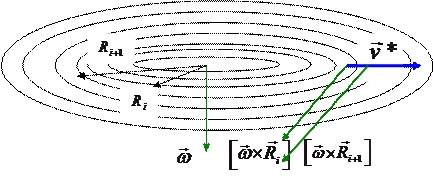
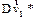 и
и