Второго порядка с постоянными коэффициентами

Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентам  называется уравнение вида:

  у ² + p y ¢ + qy = 0,

где p , q – постоянные величины.

Для линейных однородных дифференциальных уравнений второго порядка формулируется задачаКоши :

 найти решение у = у(х) уравнения, удовлетворяющее

начальным условиям у(х ₀) = у ₀, у ¢ (х₀) = у ¢ ₀ . Это значит, что при любых начальных данных х ₀ ,у ₀ ,у ¢ ₀ существует единственное решение  у = у(х) дифференциального уравнения, удовлетворяющее начальным условиям.

       Решение данного дифференциального уравнения находится в виде  линейной комбинации двух частных решений :

                                 у = С₁у ₁+ С ₂ у_{2 .}

              Эта линейная комбинация называется общимрешением.

Частное решение ищется в виде у = ℮ ^kx  ,где k = const.

Продифференцировав частное решение и подставив первую и вторую производные в дифференциальное уравнение, получим:  

                              ℮ ^kx (k ²+ pk + q) = 0

 

        Так как ℮ ^kx ≠ 0,  то

                             k ² + pk + q = 0 – характеристическое уравнение линейного однородного дифференциального уравнения.

   Решив характеристическое уравнение, найдем его корни и запишем два частных решения.

    При решении характеристического уравнения возможны три случая.

     Случай 1. Корни характеристического уравнения действительные и различные: k ₁ ≠ k ₂ . В этом случае имеем два частных решения. Общее решение уравнения имеет вид:

       

                    y = С₁ ℮  + С ₂ ℮  

 

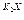
    Случай 2. Корни характеристического уравнения действительные и равные:

k ₁ = k ₂ . В этом случае находится одно частное решение. Общее решение уравнения имеет вид:

     

у =  ℮ ^kx ( С₁ + С ₂х)

    Случай 3. В третьем случае корни характеристического уравнения комплексные числа.

k ₁ = a + bi k ₂ = a - bi

Общее решение уравнения имеет вид:

 

у= ℮ ^ax ( C ₁ cos bx + C ₂ sin bx ).

 

Дифференциальное уравнение гармонических колебаний является дифференциальным уравнением второго порядка и широко встречается на практике. Решение дифференциального уравнения гармонических колебаний имеет

вид:

х = А sin ( w t + j ), где А – амплитуда колебаний, w - частота колебаний, j - начальная фаза гармонического колебания.

 

---

Дата добавления: 2018-10-27; просмотров: 117; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!