Многоканальная СМО с неограниченной очередью

⇐ ПредыдущаяСтр 4 из 4

Многоканальная СМО – это система с несколькими одинаковыми устройствами обслуживания) изображена на рис. 3.5.

Рис. 3.5. Многоканальная СМО

Рис.3.6

Найдём вероятности p_k:

Для состояния S ₀: ;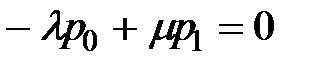

Для состояний S ₁ – S_n: ;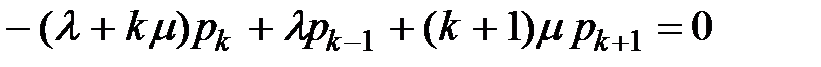

Для S_n ₊₁: ; ...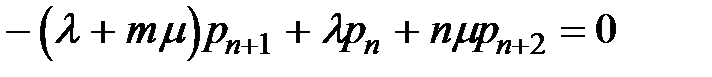

Для S_n ₊ _s _-1: ;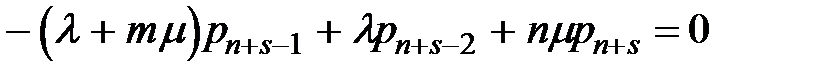

Для S_n ₊ _s: .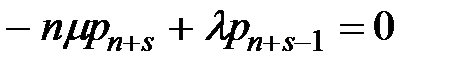

Из первых n+1 уравнений получаем: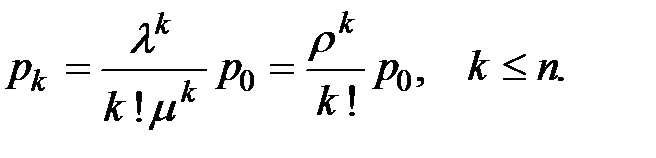

Из последнего уравнения выражаем: 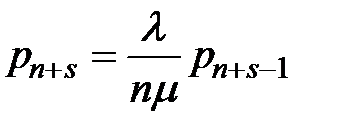и подставляем в предпоследнее: 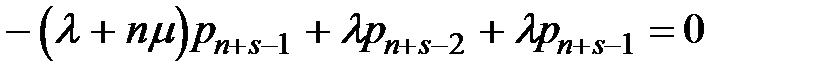, 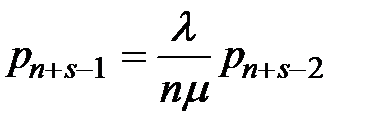. Тогда .

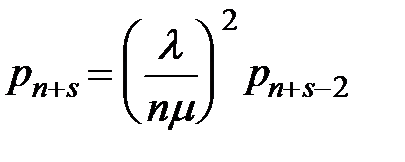Продолжая аналогию: .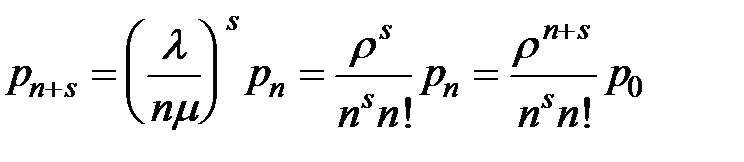

Теперь найдём p ₀, подставив полученные выражения в нормировочное условие ( 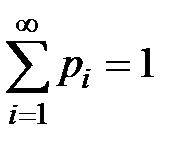): 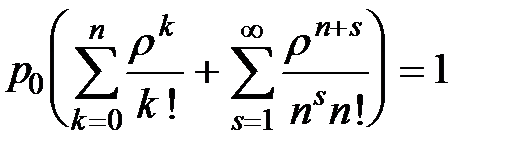. Отсюда .

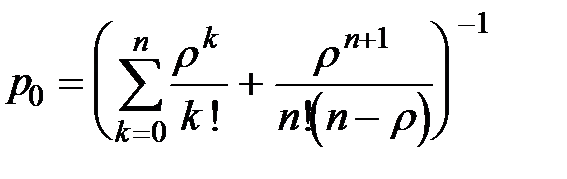Лекция 4

Показатели эффективности СМО

– Вероятность потери требования в СМО. Особенно часто ею пользуются при исследовании военных вопросов. Например, при оценке эффективности противовоздушной обороны объекта она характеризует вероятность прорыва воздушных целей к объекту. Применительно к СМО с потерями она равна вероятности занятости обслуживанием требований всех n приборов системы. Чаще всего эту вероятность обозначают p_n или p _отк.

– Вероятность того, что обслуживанием требований в системе занято k приборов, равна p_k.

– Среднее число занятых приборов: 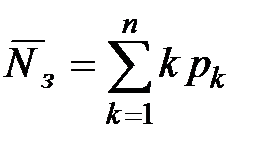характеризует степень загрузки обслуживающей системы.

– Среднее число свободных от обслуживания приборов: .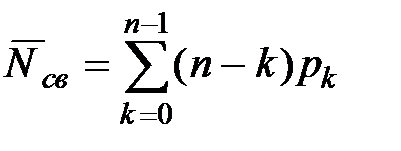

– Коэффициент простоя приборов: .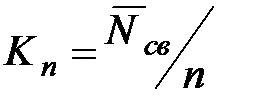

– Коэффициент занятости оборудования: .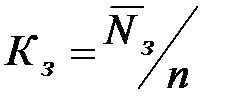

– Средняя длина очереди: 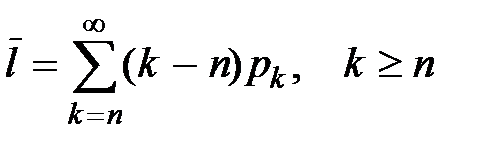, p_k - вероятность того, что в системе находится k требований.

– Среднее число заявок, находящихся в сфере обслуживания: .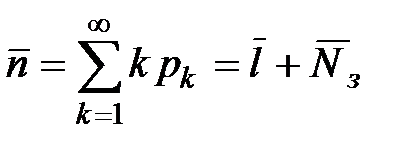

– Вероятность того, что число заявок в очереди, ожидающих начала обслуживания, больше некоторого числа m: 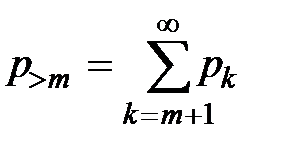. Этот показатель особенно необходим при оценке возможностей размещения требований при ограниченности времени для ожидания.

Кроме перечисленных критериев при оценке эффективности СМО могут быть использованы стоимостные показатели:

q _об – стоимость обслуживания каждого требования в системе;

q _ож – стоимость потерь, связанных с простаиванием заявок в очереди в единицу времени;

q _у – убытки, связанные с уходом из системы заявки;

q_k – стоимость эксплуатации каждого прибора в единицу времени;

q^k _пр – стоимость простоя единицы времени k-го прибора системы.

При выборе оптимальных параметров СМО по экономическим показателям можно использовать функцию стоимости потерь в системе (для СМО с ожиданием): 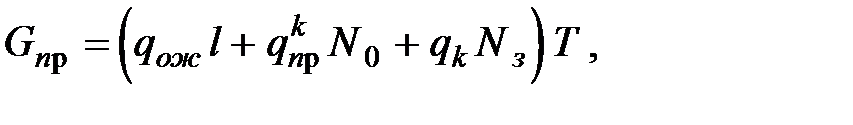T – интервал времени.

Для СМО с отказами: .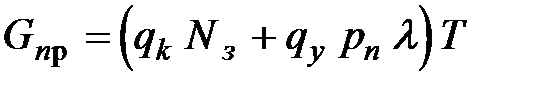

Для смешанных: .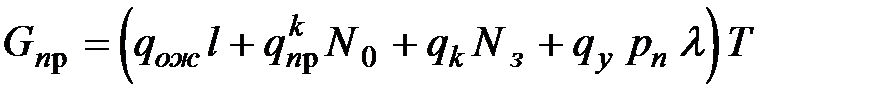

Критерий экономической эффективности СМО: 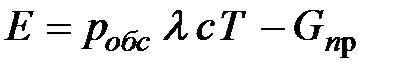, с – экономический эффект, получаемый при обслуживании каждой заявки.

СМО замкнутого типа

Пример. С1, С2, С3 – станки; НЦ – центральный накопитель; B – манипулятор. Транспортная тележка (манипулятор) транспортирует отработанную деталь от станка к накопителю и укладывает её там, забирает новую деталь (заготовку), транспортирует её к станку и устанавливает в рабочую позицию для зажима. Во время всего периода, необходимого для выгрузки–загрузки, станок простаивает. Время T _з смены заготовки и есть время обслуживания.

Интенсивность обслуживания станков определяется как 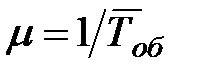, 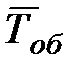– среднее время обслуживания станка, которое вычисляется как 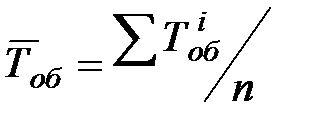, где n – число заявок. Интенсивность подачи станком заявки на обслуживание определяется как 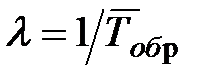(где 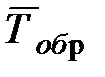– среднее время обработки детали станком).

Станочная система с однозахватным манипулятором представляет собой СМО с ожиданием с внутренней организацией FIFO: каждая заявка станка на обслуживание удовлетворяется, в случае когда манипулятор занят, заявка становится в очередь и станок ожидает когда манипулятор освободится. Данный процесс марковский, т.е. случайная выдача заявки на обслуживание в определённый момент времени t ₀ не зависит от предыдущих заявок, т.е. от течения процесса в предшествующий период. Продолжительность исполнения заявки может быть различной и является случайной величиной, не зависящей от числа поданных заявок. Весь процесс не зависит от того, что произошло ранее момента времени t ₀.

В станочной системе число заявок на обслуживание может быть равно 0, 1, 2, ... m, где m – общее число станков. Тогда возможны следующие состояния:

S ₀ – все станки работают, манипулятор стоит.

S ₁ – все станки, кроме одного, работают, манипулятор обслуживает станок, от которого поступила заявка на смену заготовок.

S ₂ – работают m -2 станка, на одном станке идет смена заготовки, другой ожидает.

S ₃ – работают m -2 станка, один станок обслуживается манипулятором, два станка ожидают в очереди.

S_m – все станки стоят, один обслуживается манипулятором, остальные ожидают очереди исполнения заказа.

Рис.4.1.

Вероятность перехода в состояние S_k из одного из возможных состояний S ₁ , S ₂ , ... S_m зависит от случайного поступления заявок на обслуживание и вычисляется как:

;

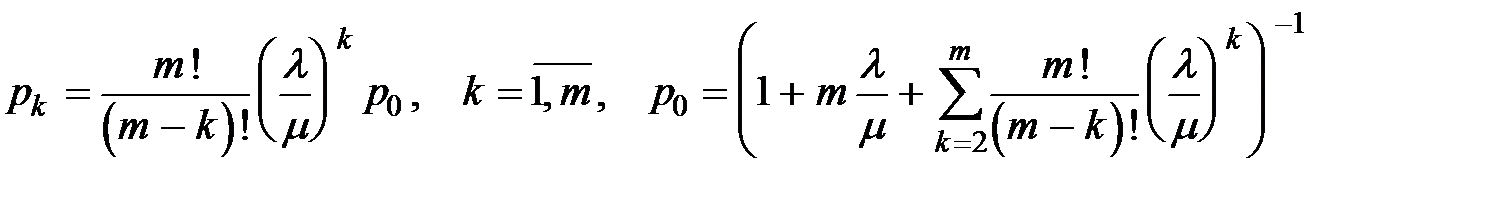p ₀ – вероятность того, что все станки работают.

Манипулятор работает при состояниях системы от S ₁ до S_m. Тогда вероятность его загрузки равна: .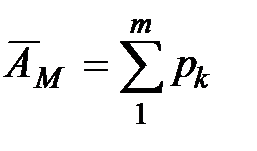

Число станков, находящихся в очереди связано с состояниями S ₂ , – S_m, при этом один станок обслуживается, а (k-1) – ожидают. Тогда, среднее число станков в очереди: .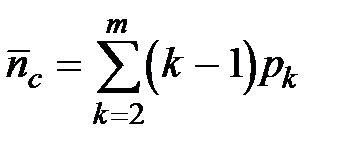

Коэффициент простоя одного станка (из-за ожидания при многостаночном обслуживании): .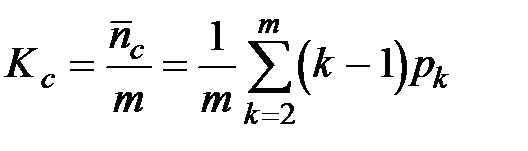

Среднее использование одного станка:

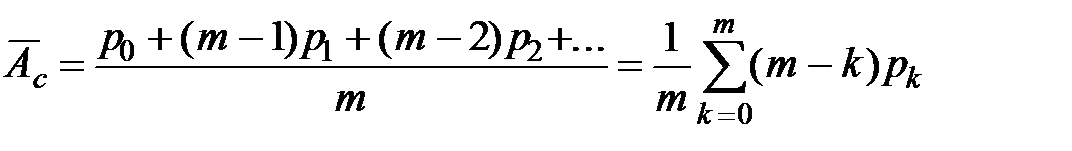Применение метода Монте-Карло для решения задач,
связанных с теорией массового обслуживания

Для того, чтобы описать поток однородных событий, достаточно знать закон распределения моментов времени t ₁ , t ₂ ,, ..., t_k, ..., в которые поступают события.

Для удобства дальнейших рассмотрений целесообразно от величин t ₁ , t ₂ ,, ..., перейти к случайным величинам z ₁ , z ₂ ,,..., z _m, ... , таким образом, что:

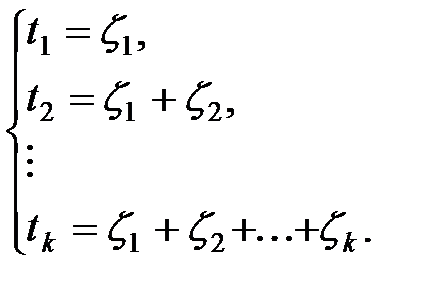
Случайные величины z _k являются длинами интервалов времени между последовательными моментами t_k.

Совокупность случайных величин z _i считается заданной, если определена совместная функция распределения:

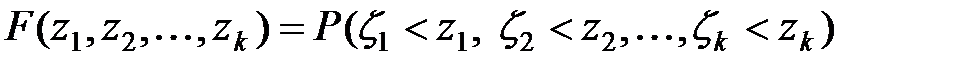Обычно рассматриваются только непрерывные случайные величины z _k, поэтому часто пользуются соответствующей функцией плотности f ( z ₁ , z ₂ ,..., z_k ).

Обычно в теории СМО рассматриваются потоки однородных событий без последействия, для которых случайные величины z _k независимы. Поэтому 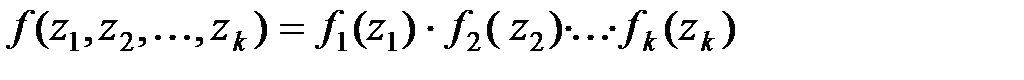. Функции f_i ( z_i ) при i >1 представляют собой условные функции плотности при условии, что в начальный момент интервала z _k ( i >1) поступила заявка. В отличие от этого функция f ₁ ( z ₁ ) является безусловной функцией плотности, т.к. относительно появления или непоявления заявки в начальный момент времени не делается никаких предположений.

Широкое применение имеют так называемые стационарные потоки, для которых вероятностный режим их во времени не изменяется (т.е. вероятность появления k заявок за промежуток времени (t ₀ , t ₀ + t) не зависит от t ₀, а зависит только от t и k). Для стационарных потоков без последействия имеют место соотношения:

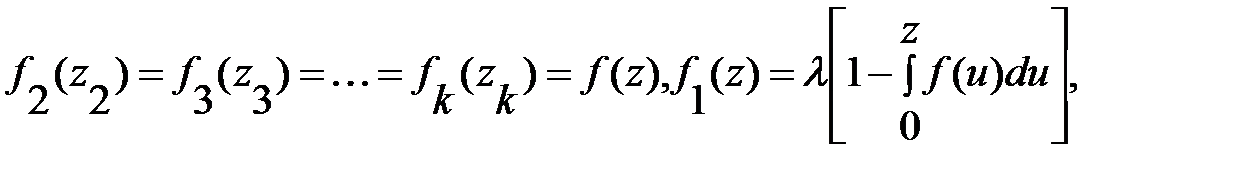
где l – плотность стационарного потока.

Поступившая в систему заявка может занимать только свободные линии. Относительно порядка занятия линий могут быть сделаны различные предположения:

а) линии занимаются в порядке их номеров. Линия с большим номером не может быть привлечена к обслуживанию заявки, если имеется свободная линии с меньшим номером;

б) линии занимаются в порядке очереди. Освободившаяся линия поступает в очередь и не начинает обслуживания заявок до израсходования всех ранее освободившихся линий;

в) линии занимаются в случайном порядке в соответствии с заданными вероятностями. Если в момент поступления очередной заявки имеется n _св свободных линий, то в простейшем случае вероятность занять некоторую определённую линию может быть принята равной 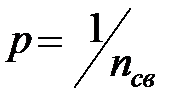. В более сложных случаях вероятности 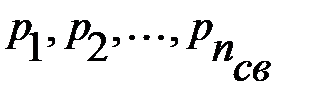считаются зависящими от номеров линий, моментов их освобождения и других параметров.

Аналогичные предположения можно сделать и относительно порядка принятия заявок к обслуживанию в том случае, когда в системе образуется очередь заявок:

а) заявки принимаются к обслуживанию в порядке очереди. Освободившаяся линия приступает к обслуживанию той заявки, которая ранее другой поступила в систему;

б) заявки принимаются к обслуживанию по минимальному времени получения отказа. Освободившаяся линия приступает к обслуживанию той заявки, которая в кратчайшее время может получить отказ;

в) заявки принимаются к обслуживанию в случайном порядке в соответствии с заданными вероятностями. Если в момент освобождения линии имеется m заявок в очереди, то в простейшем случае вероятность выбрать для обслуживания некоторую определённую заявку может быть принята равной q =1/ m. В более сложных случаях вероятности q ₁ , q ₂ ,..., q_m считаются зависящими от времени пребывания заявки в системе, времени , остающегося до получения отказа и других параметров.

Для решения ряда прикладных задач оказывается необходимым учитывать такой важный фактор, как надёжность элементов обслуживающей системы. Будем предполагать, что с точки зрения надёжности каждая линия в данный момент времени может быть либо исправной, либо неисправной. Надёжность линии определяется вероятностью безотказной работы R= R( t), задаваемой как функция времени. Будем также предполагать, что линия, вышедшая из строя по причине неполной надёжности, может быть введена в строй (отремонтирована), для чего требуется затратить время t _p. Величину t _p будем считать случайной величиной с заданным законом распределения.

Относительно судьбы заявки, при обслуживании которой линия выходит из строя, могут быть сделаны различные предположения: заявка получает отказ; заявка остаётся в системе (с общим временем пребывания в системе не более t _n) как претендент на обслуживание вне очереди; заявка поступает в очередь и обслуживается на общих основаниях и т.д.

Сущность метода статистических испытаний применительно к задачам массового обслуживания состоит в следующем. Строятся алгоритмы, при помощи которых можно вырабатывать случайные реализации заданных потоков однородных событий, а также «моделировать» процессы функционирования обслуживающих систем. Эти алгоритмы используются для многократного воспроизведения реализаций случайного процесса обслуживания при фиксированных условиях задачи. Получаемая при этом информация о состояниях процесса подвергается статистической обработке с целью оценки, являющихся показателями качества обслуживания.

Метод статистических испытаний позволяет более полно, по сравнению с асимптотическими формулами, исследовать зависимость качества обслуживания от характеристик потока заявок и параметров обслуживающей системы.

Это достигается благодаря двум обстоятельствам. Во-первых, при решении задач теории массового обслуживания методом статистических испытаний может быть использована более обширная информация о процессе, чем это обычно удаётся сделать, применяя аналитические методы.

С другой стороны, значения показателей качества обслуживания, получаемые из асимптотических формул, строго говоря, относятся к моментам времени, достаточно удалённым от начала процесса. Реально, для моментов времени, близких к началу процесса, когда ещё не наступил стационарный режим, значения показателей качества обслуживания в общем случае существенно отличаются от асимптотических значений. Метод статистических испытаний позволяет достаточно обстоятельно изучать переходные режимы.

Для многих прикладных задач предположения, при которых справедливы аналитические формулы, оказываются слишком стеснительными. При решении задач методом статистических испытаний некоторые предположения могут быть существенно ослаблены.

В первую очередь это относится к многофазному обслуживанию (т.е. рассматриваются обслуживающие системы, состоящие из нескольких последовательно действующих в общем случае неоднотипных агрегатов).

Другим важным обобщением задачи является предположение о характере потока заявок, поступающих на обслуживание. Допускается рассмотрение потоков однородных событий с практически произвольным законом распределения. Последнее обстоятельство оказывается существенным по следующим двум причинам. Во-первых, реальные потоки заявок в некоторых случаях заметно отличаются от простейшего. Для пояснения второй причины предположим, что исходный поток заявок достаточно точно аппроксимируется простейшим потоком. При этом поток заявок, обслуженных на первой фазе, уже, строго говоря не будет простейшим. Поскольку поток, являющийся выходным для первой фазы, будет входным потоком для агрегата, обслуживающего заявки на второй фазе, мы снова приходим к задаче обслуживания потоков, не являющимися простейшими.

Структура алгоритма, моделирующего
процесс обслуживания заявок

Рассмотрим однофазную СМО, имеющую n линий, на которые поступают заявки в случайные моменты времени t_i. Если в момент поступления заявки оказываются в наличии свободные линии (их число n _св), заявка занимает одну из них на время t _p. В противном случае заявка находится в системе до момента t_n , ожидая обслуживания. В течение времени ожидания некоторые линии могут освободиться (их число m), и в этом случае будет возможность обслужить заявку. Если до момента времени t_n ни одна из линий не освобождается (m =0), заявка получает отказ.

Будем считать, что в силу недостаточно высокой надёжности системы, линии обслуживающие заявку, могут выходить из строя, тогда заявка получает отказ, а линия может быть отремонтирована и через промежуток времени t_pem введена в строй.

Для исследования качества обслуживания заявок предусматривается N ^* кратное моделирование процесса функционирования системы в интервале (0, T ). В процессе моделирования число обследованных реализаций обозначим через N.

Алгоритм:

1. Определяется момент t_i поступления очередной заявки в систему.

2. Если t_i < T, то переход на шаг 3, иначе – на шаг 11.

3. Проверка возможности обслужить поступившую заявку: если n _св >0, то переход на шаг 4, иначе – на шаг 12. (Значение времени поступления заявки t_i сравнивается с t _осв для всех линий, т.о. выявляются свободные линии.)

4.Если n _св >1, то переход на шаг 5, иначе – на шаг 6.

5. Выбирается номер свободной линии по специальным правилам.

6. Назначается выбранная линия.

7. Проверка: имеет ли место срыв обслуживания по причине недостаточной надёжности? Если да, то переход на шаг 8, иначе – на шаг 10.

8. Определение времени t _рем ремонта линии, вышедшей из строя (t _рем имеет определённый закон распределения).

9. N _отк = N _отк +1. Переход на шаг 1.

10. Определение времени занятости t _з линии, которая назначена обслуживать заявку (некая случайная величина с определенным законом распределения) и времени освобождения линии: t _осв = t_i + t _з. Переход к очередной заявке (шаг 1).

11. Проверка: если N < N ^*, то N = N +1 и переход на шаг 1, иначе – обработка результатов опыта и конец.

12. Определить:

а) времени t_n пребывания заявки в системе;

б) число освободившихся каналов m за время t_n.

13. Если m >0, то переход на шаг 14, иначе – на шаг 9.

14. Если m >1, то переход на шаг 15, иначе – на шаг 6.

15. Выбирается определённая линия в соответствии с принятыми правилами и переход на шаг 6.

Дата добавления: 2018-10-26; просмотров: 684; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 34

Мы поможем в написании ваших работ!