Обобщение и специализация, абстрагирование и конкретизация
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ «ВИТЕБСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ П.М. МАШЕРОВА»
Факультет _______Математический______________
(название факультета)
Кафедра ______Алгебры и МПМ________________
(название кафедры, за которой закреплена дисциплина)
КУРСОВАЯ РАБОТА
по дисциплине _____специализация_____________________
(название дисциплины)
основные мыслительные операции в познании математки в средней школе
(название темы работы заглавными буквами)
Зайцев Андрей Юрьевич,
(фамилия, имя, отчество студента (слушателя)
4 курс группа 42_________
(курс, группа)
Руководитель:
Семёнов Ефим Евстафьевич ,
(фамилия, имя, отчество)
профессор, кандидат педагогических наук
(должность, ученая степень, звание)
Витебск, 2014
| Содержание Введение 1) Общая характеристика метод научного исследования 2) Общие методы преподавания математике 2.1. Анализ и синтез 2.2. Дедукция и индукция 2.3. Обобщение и специализация, абстрагирование и конкретизация. 2.4. Сравнение и аналогия Заключение Литература | 2 3 4 5 5 11 17 19 21 22 |
Введение
Оперируя «идеальными» объектами, отражающими свойства математических приемов и законы материального мира в сочетании с отвлечением от несущественных свойств рассматриваемых объектов, математики в своих понятиях и положениях выражает наиболее глубокие и общие свойства реальной действительности.
|
|
|
Процесс познания и процесс обучения учащихся выражает самостоятельное открытие математических фактов истин, поэтому научные методы математического исследования одновременно служат и методами учебной работы учащихся.
Проблема методов обучения выражается в вопросе «как учить?», для чего необходимо:
1) выяснить, для чего это изучается, какие знания, умения и навыки должны приобрести учащиеся в результате изучения;
2) провести логико-дидактический анализ того, что изучается (структура и особенности содержания обучения; изложение в школьном учебнике);
3) знать объект обучения (уровень мыслительной деятельности учащихся, объем знаний, умений и навыков, необходимых для обучения по данному содержанию).
Общая характеристика методов научного исследования
Различают традиционные и современные методы обучения. Традиционные методы направлены на обучение готовым знаниям и учебная деятельность учащихся носит репродуктивный характер, и не способствует эффективному развитию. Внешне традиционный метод проявляется в хорошо известной форме, когда учитель излагает учебный материал с привлечением различных средств наглядности, а ученики воспринимают учебную информацию, заучивают и воспроизводят ее по требованию учителя. Учебная деятельность ученика репродуктивна, а главный результат обучения – усвоение суммы фактов. Развивающий эффект весьма низок, т.к. нет активной деятельности учеников.
|
|
|
Современные методы, которые не противопоставляются традиционным, ориентированы на обучение деятельности по самостоятельному приобретению новых знаний, на обучение познавательной деятельности, включающей следующие компоненты:
1) общие логические приемы мышления (индукция, дедукция, анализ, синтез, аналогия, обобщение, абстрагирование, конкретизация, классификация);
2) специальные приемы мыслительной деятельности, составляющие основу математических методов познания (метод построения математических моделей процессов; способов абстрагирования, присущих математике; аксиоматический метод);
3) система знаний.
Усвоение математических знаний и уровень математического развития учащихся всегда проверяется через умение решать задачи. Методы обучения, ориентированные на развитие активной познавательной деятельности учащихся, требуют научить их отыскивать и описывать общие методы (алгоритмы) решения классов задач однотипных через анализ и обобщение способов решения частных задач, принадлежащих этим классам.
|
|
|
Общие методы преподавания математике
Анализ и синтез
Анализ – логический прием, метод исследования, состоящий в том, что изучаемый объект мысленно расчленяется на составные элементы, каждый из которых исследуется в отдельности как часть расчлененного целого. Анализ – это рассуждение от неизвестного к известному (аналитическое рассуждение). Ведущий вопрос: что надо знать, чтобы ответить на поставленный вопрос?
Синтез – логический прием, с помощью которого отдельные элементы соединяются в целое. Синтетические рассуждения – это путь от данного к искомому. Ведущий вопрос: что можно узнать по данным условиям?
Анализ и синтез выступают в самых разнообразных формах: как методы решения задач, доказательства теорем, изучение свойств математических понятий и т.д.
Первоначально анализ и синтез воспринимали как методы мышления: анализ – от целого к частям целого; синтез – от частей к целому; затем как прием мышления: анализ – от следствия приходят к причине, породившей это следствие; синтез – от причины переходят к следствию, порожденному этой причиной. Это иллюстрирует арифметическое и алгебраическое решение задачи: «Маше и Тане вместе 12 лет. Тане – 5 лет. Сколько лет Маше?»
|
|
|
анализ: 12-5=7
синтез: х+5=12, х=12-5; х=7.
С точки зрения психологии, процесс мышления – это прежде всего анализирование и синтезирование того, что выделено анализом.
Формы анализа:
а) типа «фильтр» – хаотический способ решения данной задачи. Например, требуется из 6 спичек сложить 4 равносторонних треугольника (пространственное решение).
Задача: «Поверхность пруда постепенно зарастает ряской. Площадь поверхности занимаемая ряской, с каждым днем увеличивается в два раза. Весь пруд зарастает ряской в течение 100 дней. За сколько дней зарастает ряской половина поверхности пруда?»
б) анализ через синтез – объект в процессе мышления включается во все новые связи и в силу этого выступает во все новых качествах, которые фиксируются в новых понятиях; из объекта, таким образом, как бы вычерпывается все новые содержания. Например, доказать, что периметр равностороннего треугольника, описанного около окружности, вдвое больше периметра равностороннего треугольника, вписанного в эту окружность.
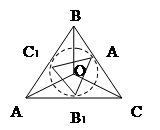
AO=R; OK=r; 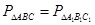 ; AB=OB
; AB=OB 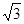 =R
=R 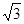 ; OB1=
; OB1= 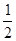 OB
OB 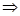 r=
r= 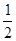 R
R 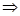 A1B1=
A1B1= 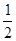 AB=
AB= 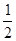 R
R 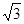

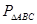 =3AB=3R
=3AB=3R 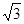 ;
; 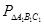 =
= 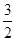 R
R 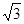 , ч.т.д.
, ч.т.д.
Рассмотрим анализ и синтез как методы изучения математики.
I а) Аналитические и синтетические методы доказательства теорем и неравенств.
Аналитический метод доказательства: исходным пунктом для обоснования требуемого утверждения является само это утверждение, которое путем логически обоснованных шагов сводится к утверждению, известному, как истинное.
Синтетический метод доказательства: отыскиваются такие истинные утверждения, которые можно было бы путем логически обоснованных шагов преобразовать в данное утверждение. Для него характерным является описание того, что делается, но не объясняется, почему берется в качестве исходного то или иное утверждение. Вот почему доказательство большинства теорем в геометрии не понятны ученика, т.к. они являются синтетическим рассуждением. Преодолеть это затруднение возможно при предварительном анализе условий и заключения теоремы, т.е. теорему следует воспринимать как обычную задачу.
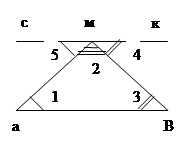 Пример: Доказать, что сумма внутренних углов в треугольнике равна 1800.
Пример: Доказать, что сумма внутренних углов в треугольнике равна 1800.
Аналитический путь: 1800–величина развернутого угла, значит, достаточно показать, что при угле любого треугольника «вложатся» в развернутый угол: строим развернутый угол при вершине M:
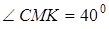 ;
;  2-есть;
2-есть;  5=
5=  1;
1;  4=
4=  3; т.к.
3; т.к.  5+
5+  2+
2+  4=1800
4=1800 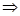
 1+
1+  2+
2+  3=1800 ч.т.д.
3=1800 ч.т.д.
Синтетический путь: проводим CK||AB;
 5=
5=  1;
1;  4=
4=  3
3 
 5+
5+  2+
2+  4=1800
4=1800 
 1+
1+  2+
2+  3=1800 ч.т.д
3=1800 ч.т.д
Пример: Доказать неравенство: 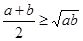 , где
, где 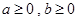 .
.
| Аналитический | Синтетический |
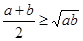
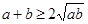
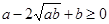
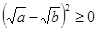 -очевидно -очевидно
| 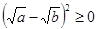
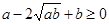
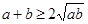
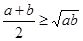 , ч.т.д. , ч.т.д.
|
Используя аналитический метод, учащийся действует сознательно и убежденно, т.к. он знает с чего начать. Но аналитический метод доказательства не всегда правомерен. Покажем это на примере простого софизма.
Пример: Доказать, что 3= -3.
Доказательство: Пусть 3=-3  32=(-3)2 – возвели почленно в квадрат
32=(-3)2 – возвели почленно в квадрат 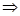 9=9 и получили истинное утверждение, значит, и исходное (требуемое) утверждение верно (!?).
9=9 и получили истинное утверждение, значит, и исходное (требуемое) утверждение верно (!?).
II. б) Восходящий анализ:
Дано: Окружность; CD, AB – хорды, AB 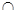 CD=M.
CD=M.
Доказать: AM∙MB=CM∙MD.
Доказательство: не известно, верно ли доказываемое равенство, но если получим пропорцию: 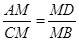 , будем иметь подобия треугольников:
, будем иметь подобия треугольников: 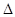 AMD~
AMD~ 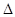 CMB. А это возможно в случае равенства соответствующих углов:
CMB. А это возможно в случае равенства соответствующих углов:
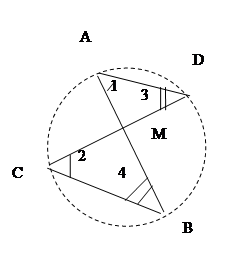
 1=
1=  2, т.е.
2, т.е.  BCD=
BCD=  BAD – как вписанные;
BAD – как вписанные;
 3=
3=  4, т.е.
4, т.е.  ADC=
ADC=  ABC – как вписанные.
ABC – как вписанные.
Восходящий анализ проиллюстрировал процесс сведения задачи к подзадачам.
Идея этого метода: для того чтобы А было верно, достаточно, чтобы было верно В и так далее.
Преимущество этого метода в процессе изучения математики: а) восходящий анализ обеспечивает сознательное и самостоятельное отыскание метода доказательства теоремы самими учащимися; б) Способствует развитию логического мышления; в) обеспечивает осознанность, целенаправленность действий на каждом этапе доказательства; г) схема метода проста: что требуется доказать? Что для этого достаточно доказать?
III. в) Нисходящий анализ.
Задача. Доказать, что квадрат медианы, проведенной к катеты прямоугольного треугольника, сложенный с утроенным квадратом половины этого катета, равен квадрату гипотенузы.
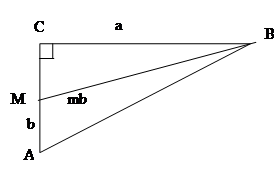
Дано: 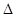 ABC,
ABC,  C=900, BM – медиана: AM=MC
C=900, BM – медиана: AM=MC
Доказать:
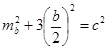 (1)
(1)
Доказательство: рассмотрим 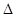 BCM. Он прямоугольный, тогда:
BCM. Он прямоугольный, тогда: 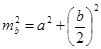 (2) в уравнение (1):
(2) в уравнение (1):
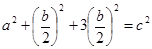 (3)
(3) 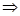
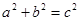 (4).
(4).
Получили второе неравенство. Но сказать, что этим самым задача решена, неверно. Нисходящий анализ приводит к синтетическому рассуждению. Для получения логического доказательства необходимо провести все рассуждения в обратном порядке.
IV. г) Анализ и синтез при решении геометрических задач на построение.
Пример: Построить прямоугольный треугольник по гипотенузе С и радиусу r вписанной в него окружности.
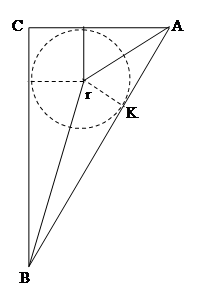
Анализ. Пусть задача решена сделаем эскиз.
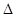 ABC построим, если построим
ABC построим, если построим 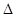 AOB;
AOB;
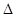 AOB построим, зная AB=C, OK=h и
AOB построим, зная AB=C, OK=h и  AOB.
AOB.
 AOB=1800-(
AOB=1800-(  A+
A+  B)/2=1800-450=1350.
B)/2=1800-450=1350.
Треугольник по данным С,  AOB, h построить можем.
AOB, h построить можем.
Синтез: Строим 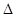 ABC, начиная с построения
ABC, начиная с построения 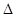 AOB по данным С,
AOB по данным С,  AOB, h.
AOB, h.
Задача. Построить четырехугольник, если даны все его четыре стороны и известно, что одна из диагоналей делит один из углов пополам.
Анализ. Пусть задача решена, сделаем эскиз.
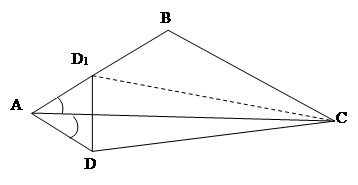
Поиск проведем через синтез, т.е. исходя из того, что нам известно:  BAC=
BAC=  CAD
CAD 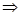 строим
строим 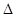 D1, симметричную D относительно AC, тогда СD1=СD
D1, симметричную D относительно AC, тогда СD1=СD 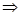
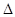 D1BC можно построить по трем сторонам, если AB=a; BC=b; CD=c; AD=d
D1BC можно построить по трем сторонам, если AB=a; BC=b; CD=c; AD=d 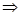 BC=b; D1C=c; D1B=a-d.
BC=b; D1C=c; D1B=a-d.
V. д) Анализ и синтез при решении текстовых задач.
Задача. Длина прямоугольного параллелепипеда 8м, ширина 6м, а высота 12 м. найдите сумму площадей его наибольшей и наименьшей граней.
Данная задача – арифметическая. Проанализируем ее. Что надо знать для того, чтобы найти требуемую сумму? – ТК она является прямоугольником, то достаточно знать его ширину и длину. Можем ли мы найти искомые площади?– Наименьшая грань – 6м и 8м, наибольшая грань – 8м и 12 м. Синтез в задаче – ее решение: 6∙8+8∙12=8∙18=144
Ответ: 144 м2.
Дедукция и индукция
Переход от частного к общему, от единичных фактов, установленных с помощью наблюдения и опыта, к обобщениям является закономерностью познания. Неотъемлемой логической формой такого перехода является индукция, представляющая собой метод рассуждений от частного к общему, вывод заключения из частных посылок (с латинского: induction – наведение).
Использование этого метода рассуждений для получения новых знаний в процессе обучения называют индуктивным методом обучения.
Индукция имеет три значения:
Вид умозаключения: 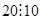 ,
, 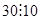 , 20 и 30 оканчиваются цифрой ноль
, 20 и 30 оканчиваются цифрой ноль 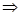 число, оканчивающиеся нулем, делятся на 10 (истинно);
число, оканчивающиеся нулем, делятся на 10 (истинно);
Метод исследования: поиск формулы простого числа: 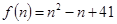
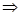
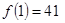 ,
, 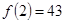 ,
, 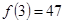 и т.д.,
и т.д., 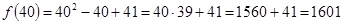 – простые числа, однако
– простые числа, однако 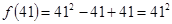 – число составное;
– число составное;
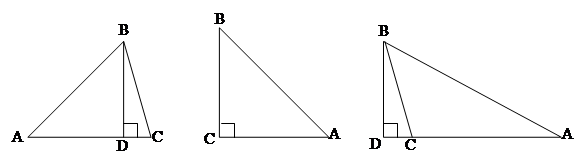
Метод обучения: знакомя учащихся с понятием о высоте треугольника, учитель чертит на доске остроугольный прямоугольный, тупоугольный треугольники и в каждом из них проводит высоту. Из рассмотрения этих чертежей учащиеся приходят к выводу, что если углы прилежащие к основанию треугольника, острые то высота пересекается с основанием, а если один из двух углов, прилежащих к основанию треугольника, тупой, то высота пересекается с продолжением этого основания.
Различают два основных вида индуктивных умозаключений: неполную и полную индукции.
Полной индукцией называется умозаключение, основанное на рассмотрении всех единичных и частных суждений (случаев), относящихся к рассматриваемой ситуации.
Единичные суждения:
· окружность может пересекаться с прямой не более чем в двух точках;
· эллипс может пересекаться с прямой не более чем в двух точках;
· парабола может пересекаться с прямой не более чем в двух точках.
Частные суждения:
Эллипс (в частности, окружность), парабола представляют собой виды конических сечений, образуя множество кривых второго порядка.
На основании этих суждений получаем новое: кривые второго порядка могут пересекаться с прямой не более чем в двух точках (истинное).
Если число случаев конечно и все они рассмотрены, то вывод, сделанный посредством полной индукции можно считать обоснованным.
Например:
от 1 до 10 четыре простых числа;
описать все возможные решения уравнения х2=а: а<0, a=0, a>0.
Таким образом, заключение, основанное на полной индукции, является достоверным и она может использоваться как метод строгого научного доказательства (теорема о величине вычисленного угла; «доказать, что запись квадрата числа натурального не может оканчиваться цифрой 7»).
Неполная индукция (как метод исследования) – индукция, при которой не исчерпываются все частные случаи, относящиеся к данной ситуации.
С точки зрения логики неполной индукцией называется умозаключение, основанное на рассмотрении одного или нескольких (но не всех) единичных или частных суждений, относящихся к рассматриваемому понятию (или системе понятий).
В процессе обучения неполная индукция проявляется, например, при изучении переместительного закона сложения, который ведется по схеме: 5+2=2+5, значит: a+b=b+a.
В процессе обучения методом неполной индукции не следует пренебрегать, т.к.
1) реализуется принцип обучения «от простого к сложному»;
2) изучение новых абстрактных понятий и суждений проходит естественным путем через опыт и наблюдение, через восприятие и представления; 3) обучает математической деятельности.
Дедукция (от латинского deductio – выведение) в широком смысле представляет собой форму мышления, состоящую в том, что новое предложение (а точнее, выраженная в нем мысль) выводится чисто логическим путем, т.е. по определенным правилам логического вывода (следования) из некоторых известных предложений (мыслей).
Дедукция есть форма умозаключения, при которой от одного общего суждения и одного частного суждения получают новое, менее общее или частное суждение. Сущность дедукции состоит в том, что данный частный (индивидуальный) случай подводится под общее положение.
Дедукция имеет три значения:
вид умозаключения:
1) умозаключение от более общего положения к менее общему (или единичному) положению (общее суждение: НОД(a, b)=1, если a и b взаимно простые числа; частное суждение: НОД(14, 15)=1 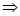 новая частное суждение: числа 14 и 15 – взаимно простые);
новая частное суждение: числа 14 и 15 – взаимно простые);
2) умозаключение от общего положения к общему положению (все частные числа кратны 2; все нечетные не кратные 2 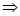 ни одно четное число не является одновременно нечетным числом);
ни одно четное число не является одновременно нечетным числом);
3) умозаключение от единичного к частному: (число 3 – простое число; число 3 натуральное число 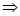 некоторые натуральные числа являются простыми).
некоторые натуральные числа являются простыми).
Метод исследования: для получения нового знания о некотором объекте (понятии, свойстве) находят ближайший к данному объекту (понятию) класс объектов (ближайшее родовое понятие), и применяют к этому объекту (понятию) существенные свойства этого класса объектов (признак рода). Например, изучая свойства квадрата, мы можем сначала установить то, что квадрат является ромбом. Следовательно, все свойства, имеющие место для ромба, имеют место и для квадрата (в частности, диагонали квадрата взаимно перпендикулярны).
Метод обучения. Включает:
1) обучение дедуктивным доказательствам и
2) обучение расширению дедуктивной системы включением в нее новых предложений, т.е. преобразованию совокупности предложений, полученных опытным путем, или с помощью индукции, аналогии или других эвристических приемов (методов), в систему предложений, упорядоченных отношением следования, расширяющую уже изученный фрагмент теории.
1) под обучением доказательству понимается обучение мыслительным процессам поиска и построения доказательства, а не воспроизведение и заучиванию готовых доказательств, т.е. учим рассуждать. Обучение поиску и построению доказательств направляется тремя основными вопросами: «Что?», «Откуда?», «Как?».
а) «Что?» – что доказывается?, каково доказываемое предложение, для которого мы ищем доказательство?, как оно формулируется?, все ли понятно в этой формулировке? Нельзя ли иначе сформулировать доказываемое предложение? Что «дано»?, что «требуется» доказать? Эти вопросы связаны с изучением доказываемого предложения, с возможным приведением его к более удобному для выяснения условий и заключения виду («вертикальные углы равны» или: если углы вертикальные, то они равны).
б) «Откуда?» – откуда, из каких посылок следует (может следовать) доказываемое предложение? Из каких же известных истинных предложений данной области (аксиом, определений, ранее доказанных теорем) можно было бы «вывести» это предложение?
в) «Как?» – как доказываемое предложение получается (выводится), из ранее известных предложений (аксиом, определений, теорем)?
В обучении доказательству выделяются два уровня:
– (V–VIII классы) – используемые в доказательствах (неявно) логические средства вывода не выявляются, не разъясняются, основное внимание уделяется выяснению того, «что доказывается» и «из чего это следует», но, не «как это следует», т.е. доказательство является рассуждением с помощью которого истинность одного предложения устанавливается на основе истинности других предложений.
– (в старших классах) – разъясняются простейшие правила вывода и на этой основе уточнено понятие доказательства.
2) в процессе обучения (опытным путем или с помощью эвристических методов) открывали, что при условии А имеет место некоторое свойство В. в таком случае придется доказать теорему: А→В. Наиболее эффективным является следующее: пусть получено некоторое множество свойств Bi . Возникает проблема выяснения логических связей между предложениями Bi и предложением А с использованием уже известных значений. Выдвигаемый в методической литературе тезис обучения «укрепленными блоками» применительно к дедуктивно построенному фрагменту учебного материала по существу означает продвижение в теорию не единичными предложениями, а маленькими теориями, описывающими определенные ситуации, фигуры и т.п.
Иллюстрацией может служить свойство точек, равноудаленных от концов отрезка.
В процессе обучения математике индукция и дедукция не выступают изолированно; они тесно переплетаются между собой.
Например: изучение переместительного закона сложения натуральных чисел учащиеся на частных примерах 2+7=7+2=9 убеждаются в справедливости свойства a+b=b 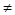 Q, используя индукцию; применяя этот закон для облегчения вычисления (1+42=42+1=43) учащиеся уже действуют дедуктивным путем.
Q, используя индукцию; применяя этот закон для облегчения вычисления (1+42=42+1=43) учащиеся уже действуют дедуктивным путем.
Метод совершенной индукции выражает взаимосвязь индукции и дедукции и используется тогда когда возникает необходимость дать логическое обоснование выводу, полученному индуктивным путем. Он осуществляется с помощью последовательно проводимых этапов:
1) наблюдение и опыт;
2) гипотеза;
3) обоснование (доказательство) гипотезы.
Например, требуется установить, сколькими способами можно совершить перестановку n элементов некоторого конечного множества.
Обобщение и специализация, абстрагирование и конкретизация
Обобщение – мысленное выделение, фиксирование каких-нибудь общих существенных свойств, принадлежащих только данному классу предметов или отношений.
Абстрагирование – это мысленное отвлечение, отделение общих, существенных свойств, выделенных в результате обобщения, от прочих несущественных (с математической точки зрения) или не общих свойств рассматриваемых предметов или отношений и отбрасывание.
Абстрагирование не может осуществляться без обобщения, без выделения того общего, существенного, что подлежит абстрагированию. Абстрагирование и обобщение неизменно применяются в процессе формирования понятий, при переходе от представлений к понятиям и, вместе с индукцией, как эвристический метод.
Под обобщением понимают также переход от единичного к общему, от менее общего к более общему.
Примеры обобщения:
1) Изучение формулы n-го члена арифметической прогрессии начинается с рассмотрения конкретных примеров на вычисление различных членов арифметической прогрессии по заданному первому ее члену и разности. При проведении этих вычислений учащиеся используют равенства: 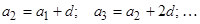 Естественно возникает полезное обобщение этих равенств в одной форму
Естественно возникает полезное обобщение этих равенств в одной форму
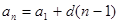 .
.
NÌZÌQÌRÌC.
При обобщении а)замене постоянной на переменную; б)снятие ограничений:
1) 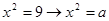
2) 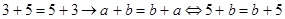
3) 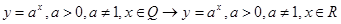
Абстрагирование:
1) параллельные прямые (линии электрических передач; линии тротуара; кромка проезжей части);
число 3 (в чувственном познании и в реальном познании).
Под конкретизацией понимают обратный переход – от более общего к менее общему, от общего к единичному. Если обобщение используется при формировании понятий, то конкретизация используется при описании конкретных ситуаций с помощью сформированных ранее понятий.
Пример:
а) наглядная иллюстрация;
б) подтверждение абстрактных понятий;
в) применение к конкретным теоремам = характеристика конкретизации.
б)1) 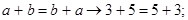
в)2) 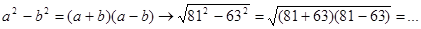
скрещивающиеся прямые (определение и отыскание их в окружающей нас действительности).
Процесс специализации – мысленное выделение некоторого свойства из множества свойств изучаемого объекта.
Например: выделяя их множества ромбов ромбы с равными диагоналями, мы получаем квадрат.
Специализация выступает как переход от данного множества к рассмотрению множества, содержащегося в данном. Специализация достигается при: а) замене переменной на постоянную 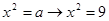
б) при введении ограничения: параллелограмм ® параллелограмм с прямым углом.
Приведу пример совместного применения наблюдения, опыта, сравнения, обобщения, абстрагирования и специализации – вывод признака делимости на 3. по схеме: число – сумма цифр – делимость суммы на 3 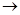 делимость числа на 3.
делимость числа на 3.
Сравнение и аналогия
Сравнение – выявление сходства и различия сравниваемых предметов.
Например,
1) треугольник и четырехугольник общим имеют соответствие числа сторон числу углов; отличие в их количестве;
2) алгебраические и обыкновенные дроби: общее – не имеют смысла при нулевом знаменателе; наличие числителя и знаменателя; различие – в природе числителей и знаменателей.
Сравнение приводит к правильному выводу, если выполняются следующие условия:
1) сравниваемые понятия однородны;
2) сравнение осуществляется по таким признакам, которые имеют для них существенное значение. Иначе говоря, основные требования к сравнению: иметь смысл; планомерно; полно.
Сравнение – почва для аналогии (греческое – соответствие, сходство), которая осуществляется по схеме:
А обладает свойствами a, b, c, d
В обладает свойствами a, b, c
Вероятно В обладает и свойством d.
Заключение по аналогии правдоподобно, но не достоверно, поэтому аналогия не является доказательным рассуждением.
Часто та или иная последовательность в изучении учебного материала обосновывается возможностью использования аналогии в обучении:
1) натуральные числа и десятичные дроби;
2) если a||b и a^b, то b^c – теорема на плоскости и в пространстве. Когда будет верным обратное утверждение: a^b и b^c Þ a||b
Поиск сходства – путь к плодотворным рассуждениям по аналогии. Например, треугольник и тетраэдр имеют сходство минимальности линий на плоскости и плоскостей в пространстве; биссектрисы треугольника пересекаются в центре вписанной в него окружности и биссекторные плоскости двугранных углов тетраэдра пересекаются в центре вписанного в него шара.
Следует различать полезную и вредную аналогии.
Полезная аналогия: прямоугольник – прямоугольный параллелепипед;
окружность – сфера;
прямая на плоскости – плоскость в пространстве.
Вредная аналогия: 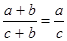 - "аналогия" с основным свойством дроби;
- "аналогия" с основным свойством дроби;
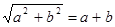 - "аналогия" с извлечением корня из произведения
- "аналогия" с извлечением корня из произведения
Заключение
Методы преподавания – упорядоченные способы взаимосвязанной деятельности учителя и учащихся, направленные на достижение целей обучения как средства образования и воспитания. Описание метода преподавания включает:
Описание обучающей деятельности учителя;
Описание учебной (познавательной) деятельности ученика;
Связь между ними или способ управления познавательной деятельности учащихся обучающей деятельностью учителя.
Система методов преподавания математике состоит из: а) общих методов обучения, разработанных дидактикой и адаптированных к обучению математике; б) частных (специальных) методов обучения математике, опережающих основные методы познания, используемые в математике. Это обусловлено тем, что:
· цели обучения включают усвоение не только определенной совокупности научных фактов, но и методов добывания этих фактов, используемых в самой науке;
· методы научных исследований – методы приобретения новых знаний в науке, методы обучения – методы приобретения новых знаний в познавательной деятельности;
· специальные методы обучения, отражающие методы самой математики, способствуют формированию и развитию математического мышления учащихся.
Литература
1. К.О. Ананченко «Общая методика преподавания математики в школе», Мн., «Унiверсiтэцкае»,1997г.
2. Н.М.Рогановский «Методика преподавания в средней школе», Мн., «Высшая школа», 1990г.
3. Г.Фройденталь «Математика как педагогическая задача»,М., «Просвещение», 1998г.
4. Н.Н. «Математическая лаборатория», М., «Просвещение», 1997г.
5. Ю.М.Колягин «Методика преподавания математики в средней школе», М., «Просвещение», 1999г.
6. А.А.Столяр «Логические проблемы преподавания математики», Мн., «Высшая школа», 2000г.
Дата добавления: 2018-10-26; просмотров: 869; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
