Почему футболисты похожи на прусских коней
Для того чтобы объяснить, как случайность и шанс позволяют нам прогнозировать, что может случиться во время матчей лиги в течение сезона, нам придется сделать одно странное отступление: заглянуть в конюшню прусской военной кавалерии конца девятнадцатого века и познакомиться с мыслями русского экономиста через теории французского математика.
Как и профессиональные футболисты, кавалерийские лошади время от времени взбрыкивают. Когда они это делают, последствия могут быть более серьезными, чем травмы, полученные в стычке на футбольном поле, прусской армии удалось это выяснить за 20 лет начиная с 1875 года. В этот период 196 солдат нашли смерть под копытами своих верных коней. Должно быть, это были абсолютно случайные события: военные должны были достаточно хорошо знать лошадей, чтобы определить, когда боевые лошади пугались, нервничали или оказывались под обстрелом, и армии не было смысла признавать, что ее солдаты систематически допускали ошибки и были сами виноваты в собственных смертях. Нет, каждая смерть была случайной и бессмысленной – например, злосчастный пруссак оказывался не в том месте и не в то время. Никакой закономерности – просто случайность.
Но русский политический экономист польского происхождения Владислав Борткевич в конце девятнадцатого века собрал данные о смертях от копыт лошадей, что позволило по-другому взглянуть на кажущуюся произвольность смертельных случаев4. Он создал знаменитую таблицу данных с 280 ячейками (14 кавалерийских корпусов на 20 лет), где демонстрировалось ежегодное количество смертей в каждом корпусе. Когда он посмотрел на ячейки, то очень быстро заметил, что их большая часть (51 процент) пуста, это означало, что в данном корпусе в данном году смертей не было. В почти трети ячеек была отмечена одна смерть, в 11 процентах – две, в четырех процентах – три, в двух ячейках – четыре, и ни в одной ячейке не было пяти или более смертей.
|
|
|
После достаточно долгого изучения таблицы Борткевич пришел к выводу, что в, казалось бы, бессистемных случаях есть логика, что в хаотичности есть системность. Проницательность русского ученого подсказала ему воспользоваться формулой распределения случайных величин, выведенной французским математиком Симеоном Дени Пуассоном. В своей работе Recherches sur la probabilitй des jugements en matiиre criminelle et en matiиre civile («Исследование о вероятности приговоров в уголовных и гражданских делах») Пуассон попытался математически описать количество совпадений, которое может произойти, если пара за парой 52 раза переворачивать верхние карты в двух перетасованных колодах5.
Используя свои данные о кавалерии, Борткевич обнаружил кое-что, чего не заметил француз: распределение Пуассона могло дать начало закону малых чисел, прогнозированию того, сколько раз определенное редкое событие может случиться в заданное время или в заданном месте. Мы можем прогнозировать общую частоту и распределение случайных событий (как часто они происходят и насколько вероятно, что они произойдут), если пытаемся проанализировать событие, которое случается нечасто, но регулярно и достаточно независимо для того, чтобы разработать основной коэффициент6.
|
|
|
Удар лошадиным копытом является одним из таких событий. По данным Борткевича, смерть под копытами прусских военных коней происходила с коэффициентом около 0,70 на каждый корпус в год. Сочетая эти данные с распределением Пуассона, Борткевич обнаружил примечательное совпадение между действительным распределением смертей и прогнозируемым распределением. Другими словами, формула Борткевича становится для нас способом предсказывать редкие и случайные события.
Что это значит? Это значит, что то, что кажется бессмысленным, случайным, на самом деле обладает предсказуемым характером. Борткевич ничего не знал о качестве сена и травы, о количестве упражнений и тренировок, о параметрах коней или разведении, о любых других параметрах, которые, по вашему мнению, могли бы оказать то или иное влияние. Все, что у него было, – основной коэффициент, информация о том, сколько смертей от ударов копыт происходило каждый год. Хотя мы не можем точно спрогнозировать, когда именно произойдет удар копытом, мы можем с большой вероятностью предположить их общее количество . Редкое и случайное абсолютно прогнозируемо; мы точно знаем, сколько этих случаев произойдет. Случайность логична, как и говорил Кройф.
|
|
|
Статистики применяют распределение Пуассона ко многим редким событиям: попадания «Фау-2» в Лондон во время Второй мировой войны, частота дорожно-транспортных происшествий, радиоактивный распад и т. д.
А имеет ли это какое-нибудь значение для футбола? Да, в точности так же, как удары лошадиных копыт, немецкие бомбы и коэффициент радиоактивного распада, голы редки (насколько редки, мы обсудим позже), но постоянны и независимы. На первый взгляд каждый из них случаен. Если рассматривать каждый в отдельности, они непредсказуемы. И именно это делает их столь восхитительными.
Но если взять среднее число голов за матч – 2,66 для матчей высших дивизионов в Англии, Германии, Испании, Италии и Франции между 1993 и 2011 годами – и применить распределение Пуассона, мы можем рассчитать, сколько игр за последние семнадцать лет были без голов, сколько – с одним голом, сколько – с двумя и так далее. Нам не требуется знать хоть что-нибудь о тактических построениях, тактике, составах команд, травмах, тренере или болельщиках, ни о чем из этого, чтобы обнаружить, что голевые моменты обладают структурой. Возможно, футбол вероятностный, но все же прогнозируемый.
|
|
|
Эта прогнозируемость означает, что, если говорить о следующем сезоне Премьер-лиги, мы знаем, что около тридцати матчей закончатся без гола, в семидесяти будет забит всего один гол, в девяноста пяти будет в целом два гола, в восьмидесяти – три, в пятидесяти пяти – четыре, а в пятидесяти по-настоящему замечательных матчей будет забито пять или более голов.
Как мы это узнали? Итак, в сезоне 380 матчей и команды забивают около 1000 голов. Благодаря тем самым лягающимся лошадям, французскому математику и русскому экономисту у нас есть все, что необходимо знать, чтобы извлечь логику из случайности.
Распределение Пуассона также может применяться к отдельным результатам матчей.
ДИАГРАММА 5
РАСПРЕДЕЛЕНИЕ СМЕРТЕЛЬНЫХ УДАРОВ КОПЫТАМИ ПРУССКИХ ВОЕННЫХ КОНЕЙ

ДИАГРАММА 6
РАСПРЕДЕЛЕНИЕ ГОЛОВ В ЕВРОПЕЙСКОМ ФУТБОЛЕ, 1993–2011 ГГ.

Возьмем среднестатистическую субботу Премьер-лиги. 7 ноября 2010 года результаты матчей были следующими: 2:2, 2:1, 2:2, 4:2, 1:1, 2:1, 2:0. Ничего экстраординарного, но насколько обычными окажутся эти результаты, если мы сравним их со многими субботами во многих сезонах нескольких лиг? Являются ли победы «Манчестер юнайтед» и «Блэкберна» со счетом 2:1, зарегистрированные в этот день, более вероятными, чем победа «Сандерленда» над «Стоком» со счетом 2:0?
Данные, предоставленные Infostrada, спортивной медиагруппой из Нидерландов, позволяют нам рассчитать частоту (в процентах) различных исходов матчей, чтобы обнаружить самый распространенный и самый редкий результаты матчей десяти сезонов Премьер-лиги, сыгранных между 2001 и 2011 годами.
Таблица 1. Результаты матчей в процентах, Премьер-лига, 2001/02–2010/11


Примечание. *Строки и столбцы могут не суммироваться точно из-за округления.
Самый распространенный результат матча – ничья со счетом 1:1, это происходит в 11,63 процента случаев, следом с небольшим отрывом идут победы со счетом 1:0, 2:1 и 2:0 на своем поле, нулевая ничья и победа со счетом 1:0 на чужом поле.
Голы действительно являются редкими и ценными событиями: более 30 процентов матчей заканчиваются с одним голом или без голов. Немного менее половины всех матчей заканчиваются тем, что хозяева поля забивают один или два гола и выигрывают, затем идет группа смешанных побед на своем и чужом поле и ничьих с достаточно результативным счетом (1:2, 3:1, 2:2), каждая из которых случается примерно в 5 процентах матчей. Наконец, существуют любые другие варианты. В выбранный нами уикенд только один результат был по-настоящему необычным: победа «Болтона» над «Спуром» со счетом 4:2.
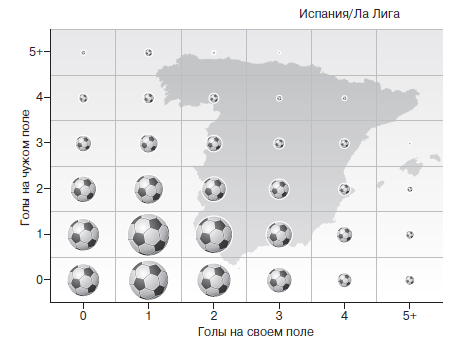
Это распределение результатов в английской Премьер-лиге, как показано на диаграммах 7–10 (размер футбольного мяча пропорционален количеству матчей), не имеет принципиальных отличий от наблюдаемых в высших континентальных лигах в течение последнего десятилетия. Это может показаться странным. Разве тот футбол, в который играют в Испании, не отличается от того, в который играют в Англии? Разве передвижения испанцев и южноамериканцев, играющих в командах Южной Европы, не принципиально отличны от бега более неуклюжих саксонцев, кельтов и скандинавов, играющих на севере? И все же, если вы сравните результаты четырех крупнейших европейских лиг в любой произвольный уикенд, они покажут, что значительной разницы нет.
ДИАГРАММА 7
САМЫЕ РАСПРОСТРАНЕННЫЕ РЕЗУЛЬТАТЫ МАТЧЕЙ В ПРЕМЬЕР-ЛИГЕ
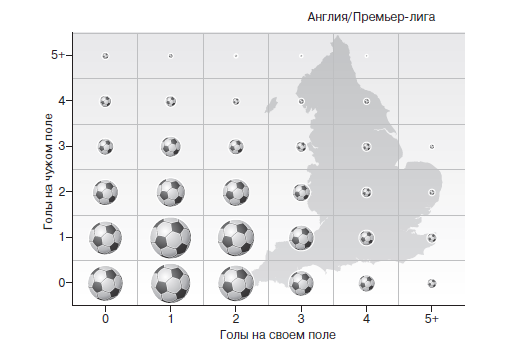
ДИАГРАММА 8
САМЫЕ РАСПРОСТРАНЕННЫЕ РЕЗУЛЬТАТЫ МАТЧЕЙ В БУНДЕСЛИГЕ

Это может удивить любителей футбола, но не ученых, занимающихся игрой. Все эти результаты очень точно отражают распределение Пуассона. Возможно множество исходов матчей, но не все результаты одинаково вероятны. На самом деле, если верить формуле, 7,7 процента матчей должны заканчиваться нулевой ничьей, а не 8,34 процента, как в Премьер-лиге, и 19,7, а не 18,5 процента должны заканчиваться всего одним голом. Но эти результаты очень близки.
Таким образом, формула больше подходит для ударов лошадиных копыт, чем человеческих ног, но это может объясняться важностью матчей, сыгранных вничью, в футболе. Количество нулевых ничьих и ничьих с результатом 1:1 больше, чем мог бы ожидать Пуассон. Степень случайности во время игры на «Вестфаленштадион» дортмундской «Боруссии» немного сложнее по сравнению с той, что существовала в давно забытых прусских конюшнях. Мяч отскакивает более беспорядочно, чем взбрыкивающий конь.
Не подлежит сомнению, что на уровне сезонов и лиг в случайности голов есть математическая логика. Это факт футбольной жизни. Это может утешить тренеров и подбодрить игроков, но то, что действительно волнует фанатов, находится на другой стороне медали: насколько значительную роль шанс будет играть в том матче, который вы собираетесь смотреть в эти выходные? Ваша команда выиграет или проиграет из-за своих способностей (или их отсутствия) или будет просто заложницей судьбы?
Что знают букмекеры?
Финальный матч Лиги чемпионов 2005 года против «Милана» был всего лишь одним из более 5000 матчей, сыгранных «Ливерпулем». Но все же впервые за 112 лет своего существования клуб смог оправиться после трех забитых ему голов. Неудивительно, что фанаты считают «стамбульское чудо» священным.
ДИАГРАММА 10
САМЫЕ РАСПРОСТРАНЕННЫЕ РЕЗУЛЬТАТЫ МАТЧЕЙ В ЛА ЛИГЕ
Такие результаты редки, но их вряд ли можно назвать беспрецедентными, и, разумеется, они не являются чудесными. В 1954 году Австрия выступила еще лучше «Ливерпуля», придя в себя после трех забитых за три минуты голов и победив Швейцарию со счетом 7:5 в матче чемпионата мира; «Чарльтон» однажды победил «Хаддерсфилд» (тренером которого в те времена был Билл Шенкли) со счетом 7:6 после того, как ему забили четыре гола. Эйсебио лично организовал волевую победу португальцев в матче против Северной Кореи на чемпионате мира 1966 года, забив три гола после того, как Португалия проигрывала со счетом 0:3. Примеры можно приводить бесконечно: «Тоттенхэм», к перерыву забивший три гола в матче с «Манчестер юнайтед» в 2000 году, но проигравший со счетом 3:5, Кевин-Принс Боатенг, забивший три мяча подряд «Лечче», играя за «Милан» в 2011 году в южной Италии, после того как его команда пропустила три гола.
Наша информация о матчах на всей территории Европы показывает, насколько редки такие случаи, но то, что они вообще происходят, обуславливается законом больших (а не малых) чисел, который вывел Якоб Бернулли, швейцарский статистик. Основное правило Бернулли было следующим: если вы делаете что-то достаточно долго, это может привести к любому возможному результату.
Бросим монеты: если вы кинете восемь монет одну за другой, шансы, что все восемь раз выпадет решка, кажутся очень маленькими. Конечно, вероятность выпадения решки после выбрасывания – 50/50, то есть шанс равен 1/1. А шанс выбросить восемь решек подряд? 255/1.
Но что, если вы бросали восемь монет четыре раза в неделю в течение сорока лет, за исключением пары недель в год, выпадающих на праздники? Получается, что вы кинули восемь монет 8000 раз. Это 64 000 выбрасываний. Шансы, что вы увидите восемь решек подряд, уже не столь призрачны. На самом деле, они весьма хорошие. Очень, очень хорошие. Настолько хорошие, что, если бы вы пошли к букмекеру и заключили пари, что за последние сорок лет вы как минимум один раз увидите восемь решек подряд, вам пришлось бы поставить весь ВВП США, чтобы выиграть шесть центов. Вы почти наверняка выбросите восемь решек подряд.
Почему? Потому что чем больше вы что-либо делаете, тем больше вероятность того, что вы как минимум один раз увидите самый невероятный результат. Следовательно, если вы достаточно долго играете в футбол (как «Ливерпуль»), рано или поздно вы победите после трех забитых вам голов. Или после четырех, как сделал «Ньюкасл» в матче против «Арсенала» в 2011 году или сам «Арсенал» в матче с «Редингом» в 2012-м. Здесь нет другого закона, кроме того, что есть шанс увидеть, как команда продержится непобежденной весь сезон или проиграет первые двенадцать матчей, или даже пляжный мяч станет постоянным участником матчей. В течение долгого периода времени все, что угодно, может произойти хотя бы один раз.
Мы знаем, что эти события – исключения с точки зрения статистики. Но насколько они необычны? Насколько редко вмешательство случайности становится заметным, когда она оказывает достаточное влияние, чтобы изменить ход матча, как случилось в тот вечер в Стамбуле?
Случайность – центральный элемент любого футбольного матча, и есть люди, само существование которых это доказывает. Это не тренеры, не нападающие или вратари, которые всегда присутствуют на поле, а букмекеры и профессиональные игроки, те мужчины и женщины, чьи доходы зависят от понимания того, кто выиграет и проиграет.
Карьера букмекера строится на случайности. Если бы матчи были предсказуемы, никто бы не делал ставки. Но хотя они не являются абсолютно прогнозируемыми, определенные факторы (физическая форма, травмы и тому подобное) известны заранее. Эта информация становится основой для высчитывания шансов и чаще всего делает одну команду фаворитом. Такие шансы рассказывают нам кое-что о случайности и предсказуемости в спорте.
Чем ниже шансы, тем более невероятна возможность проигрыша фаворита любого матча, и тем больше его противнику придется полагаться на удачу, чтобы победить. Когда две команды обладают аналогичными характеристиками, соревнование определяется удачей и текущей физической формой, и шансы на победу у обеих команд с точки зрения букмекера будут одинаковы7.
Учитывая это, мы взялись за изучение шансов в футболе и других видах спорта, чтобы установить, действительно ли букмекеры думают, что разные виды спорта по-разному зависят от удачи. У нас было подозрение, что букмекеры могут считать футбол уникальным. Исход футбольного матча труднее предугадать, чем результат бейсбольной игры, правда? Для того чтобы это выяснить, мы собрали информацию примерно двадцати бирж ставок, а также результаты финалов сезона 2010/11 НБА, НФЛ, Главной лиги бейсбола и гандбольной Бундеслиги Германии вместе с высшими футбольными лигами Англии, Франции, Испании, Италии и Германии, туда же мы добавили Лигу чемпионов8. Наш первый вопрос: насколько часто фавориты в разных странах и разных видах спорта заканчивают тот или иной матч победой?
В футболе это случается лишь в незначительном большинстве случаев – чуть больше половины. В гандболе, баскетболе и американском футболе фавориты выигрывают примерно две трети матчей, а в бейсболе – около 60 процентов. Другими словами, букмекеры с меньшим успехом могут выбрать фаворитов в футболе, чем в любом другом виде спорта.
Это ведет к нашему второму вопросу: почему это так? Действительно ли футбол больше зависит от удачи или просто букмекеры не могут правильно рассчитать шансы именно в этом виде спорта? Для этого нам надо установить не только вероятность того, что победит команда-фаворит, нам необходимо знать, являются ли шансы в футболе систематически различными. Может ли быть так, что фавориты реже побеждают в футболе из-за того, что они обладают лишь незначительными преимуществами, особенно по сравнению с другими видами спорта?
Не все фавориты одинаковы; некоторые пользуются перед матчем значительным предпочтением, другие – совсем незначительным. Если бы бросание монеты было видом спорта, ни в одном матче не было бы фаворита, а шансы каждой стороны победить всегда равнялись бы 1/1 или, если использовать выражение шансов, применяемое некоторыми биржами ставок, 2,09. Для сравнения: в спорте, если более умелая команда всегда выигрывает, ее шансы будут считаться как 1,0. Таким образом, при борьбе равных соперников шансы будут ближе к 2,0, если есть явный фаворит, шансы будут ближе к 1,0. То же самое относится к лиге или виду спорта: те соревнования, фавориты которых более очевидны, должны обладать оценкой около 1,0, те, где проигрыш во многом зависит от шансов на победу в борьбе, должны быть дальше от этого значения.
На диаграмме 12 показано среднее значение шансов для фаворитов в течение сезона для каждого из пяти видов спорта, описанных в диаграмме 11. Вертикальные линии показывают разброс шансов: нижняя часть линии – самый маленький шанс для крупнейшего фаворита сезона, верхняя часть линии – самый вероятный фаворит игры сезона.
Футбол очевидно очень отличается от других упомянутых видов спорта. В гандболе намного больше откровенных «неудачников», чем в футболе, а фавориты почти всегда выигрывают, среднее значение шансов – 1,28; среднее значение шансов в НБА и НФЛ – соответственно 1,42 и 1,49. В бейсболе разброс шансов более ограничен: здесь нет очевидных фаворитов, самые маленькие шансы составляют 1,24. Но в футболе средние шансы на победу для клуба-фаворита – 1,95.
ДИАГРАММА 11
КОЭФФИЦИЕНТЫ УСПЕШНОСТИ ПРЕДМАТЧЕВЫХ ФАВОРИТОВ В РАЗНЫХ ВИДАХ СПОРТА, СЕЗОН 2010/11

ДИАГРАММА 12
СРЕДНЕЕ ЗНАЧЕНИЕ И РАЗБРОС ШАНСОВ В КОМАНДНЫХ ВИДАХ СПОРТА

Что это означает в реальном выражении? В футболе почти в половине случаев фаворит на самом деле не является явным фаворитом. Почему дело обстоит так, можно объяснить двумя факторами: в футболе голы редки, а ничьи обычны. Это сочетание делает высчитывание шансов в футболе намного более сложным, вероятность победы для фаворита меньше.
Та мысль, что футбольные команды-фавориты побеждают только примерно в 50 процентах случаев, противоречит всему, что, как мы считаем, мы знаем об этой игре. Ведь матч «Манчестер юнайтед» с «Уиганом», конечно, не похож на бросание монеты? Кроме того, здесь вряд ли можно сделать однозначные выводы из информации: разве не естественно, что букмекеры ошибаются намного чаще просто потому, что футбол, в отличие от других видов спорта, обладает бóльшим количеством неочевидных фаворитов, команд, которые желают победить, но вряд ли достигнут этого в реальности?
Чтобы выяснить, действительно ли дело обстоит так, нам надо установить, побеждают ли сильные и слабые фавориты в разных пропорциях в различных видах спорта. Чтобы определить, насколько велико превосходство фаворита над его соперниками, мы вычислили разрыв между шансами на победу фаворита и шансами на победу аутсайдера.
В матчах, где соперники определяются жеребьевкой, разрыв близок к нулю, а в неудачных сочетаниях с явными фаворитами разрыв может достигать 50 или более процентных пунктов10.
Подобно рейтинговым агентствам на финансовых рынках, мы вернулись к данным и разделили игры на шесть групп на основании аналогичного уровня риска, варьирующихся от «голубых фишек» до «бросовых облигаций». «Голубыми фишками» стали игры, в которых ставка на победу фаворита даст вам гарантированный и очень небольшой выигрыш, в то время как ставка на аутсайдера, за которой последует практически невозможная победа, принесет сумму, достаточную для того, чтобы месяц содержать семью сделавшего ставку. Для каждого из этих шести срезов спортивного сезона мы определили, насколько часто побеждают пользующиеся различными преимуществами аутсайдеры. Другими словами, мы хотели обнаружить связь, как в случае ценных бумаг, между риском и отдачей. Результаты показаны на диаграмме 13.
Что нам показывает эта схема? Да, линия тренда футбола, демонстрирующая взаимосвязь между риском и отдачей для клубов в сезоне 2010/11, расположена значительно ниже линий других видов спорта, это происходит вне зависимости от того, насколько предпочитаемой может быть команда.
Возьмем фаворитов, мнение о которых на 50 процентов выше по сравнению с их противниками: в футболе они выигрывают в 65 процентах случаев, но в баскетболе они побеждают более чем в 80 процентах игр. Это же верно и для всех других аспектов риска: фаворит в футболе с меньшей вероятностью на самом деле победит в матче, чем фавориты в других видах спорта, это особенно заметно в баскетболе, бейсболе и американском футболе, где вероятность обратного составляет от десяти до пятнадцати процентов. Букмекеры явно думают, что футбол более зависит от удачи вне зависимости от того, насколько неравной может казаться борьба, а эти бизнесмены хорошо знают свой рынок11.
ДИАГРАММА 13
КАК ЧАСТО ПОБЕЖДАЮТ ФАВОРИТЫ?

Наши результаты принимают во внимание только один сезон, но даже более комплексное исследование, выполненное Эли Бен-Наимом, физиком-теоретиком Лос-Аламосской национальной лаборатории, вместе с Сидни Реднером и Федериком Васкесом из Бостонского университета, в котором использовались все исторические данные в нескольких видах спорта, привело к очень похожему выводу12.
Бен-Наим, Реднер и Васкес интересовались тем, насколько прогнозируемыми являются соревнования лиг, таким образом, их целью был подсчет вероятности неожиданных поражений. Как настоящие ученые, они выхватили расчет шансов из рук букмекеров и создали в памяти компьютера придуманные компьютерные игры, виртуальные таблицы, заполняемые управляющими уравнениями.

Множество виртуальных сезонов этих лиг позволило им вычислить нечто подобное нашему разрыву между шансами, что было основано на фиксации того, как фавориты и аутсайдеры входят в игру. Они углубились в историю, изучая матчи Высшей лиги английского футбола с 1888 года, Главной лиги бейсбола с 1901 года, Национальной хоккейной лиги с 1917-го и Национальной футбольной лиги с 1922-го. В целом они взяли 300 000 игр.
Как и мы, они обнаружили, что футбол – самый непредсказуемый вид спорта. В футболе больше «пляжных мячей» и ударов в перекладину, чем в любой другой игре. Здесь меньше беспроигрышных ситуаций и меньше аутсайдеров. Они рассмотрели более 43 000 футбольных матчей, и вероятность победы аутсайдера в них составила 45,2 процента. Это полностью отражает наши выводы.
Так что почти в половине случаев команда, которая не так уж хорошо подготовлена (или состоит из плохих игроков, или в ней много травмированных, или она просто не очень хороша), может закончить матч победой.
В поисках футбольных ученых
Незаметная для многих группа ученых, интересующихся футболом, зашла еще дальше в своих попытках точно определить, насколько большую роль играет удача в том или ином матче.
Возьмем Андреаса Хюера, химика-теоретика из Университета Мюнстера в Германии, и его помощников. Они заметили некоторое несоответствие между тем, как распределение Пуассона применяется к ударам лошадиных копыт, и тем, как оно применяется к ударам по мячу, и поставили перед собой задачу определить, почему это так13.
Одно из объяснений заключается в следующем: данные о футболе показывают, что команды, уже забившие один-два гола, с большей вероятностью забьют третий, четвертый или пятый, то есть во время матча происходит нечто, что не подпадает под уравнение Пуассона14. Возьмем матч между командами Манчестера в 2011 году, которую фанаты «Манчестер Сити» никогда не забудут, а фанаты «Манчестер юнайтед» хотели бы забыть навсегда. Являются ли четвертый, пятый и шестой голы, которые «Юнайтед» пропустил перед лицом шокированных зрителей на стадионе «Олд Траффорд», следствием того, что «Сити» обладал «импульсом», как это называют многие, говоря о футболе, или беспристрастным доказательством лучшей физической формы и мастерства соперников?
Команда Хюера применила математические и статистические методы к матчам немецкой Бундеслиги за двадцатилетний период и попыталась выяснить, что является более важным для понимания схем забивания гола: мастерство и тренированность, «динамика матча» (красные карточки, травмы, импульс) или то, что ученые называют «помехой», необъяснимые и очевидно непредсказуемые случайные действия. Эта немецкая команда пришла к выводу, что с математической точки зрения футбольный матч очень похож на то, как если бы каждая из двух команд кидала по три монеты, где три решки подряд означали гол, а «количество попыток обеих команд было установлено еще в самом начале матча, отражая их соответствующую подготовку в этом сезоне».
Другими словами, квалификация вашей команды во многом определяет количество ударов по воротам, а выполненный удар – шанс один к восьми попасть в ворота, число, которое показалось бы знакомым Чарльзу Рипу, нашему «футбольному счетоводу».
Окончательные результаты Хюера и его команды были однозначными. Они обнаружили, что победит ли команда и с каким количеством голов определяется в первую очередь удачей, вторые по важности аспекты – мастерство и подготовленность, а затем идет импульс. Та трепка, которую команда Роберто Манчини устроила своим старым соперникам, не была выражением их большего мастерства или примером того, как ход матча может пойти в пользу одной из сторон. Прежде всего «Манчестер Сити» был более везучим.
Это открытие удивляет фанатов, которые верят, что мастерство помогает команде полностью контролировать то, что происходит на поле, но его подтверждает немало других научных доказательств.
Несколько лет назад два астрофизика, Джеральд Скиннер из Университета Мэриленда в США и Гай Фриман из Уорикского университета, также заинтересовались результатами матчей15.
Используя некоторые алгебраические и комплексные методы, называемые байесовской статистикой, они поставили перед собой цель определить, как часто команда, обладающая бóльшим мастерством, действительно побеждает в футбольном матче. Или скажем по-другому: как часто «неправильная» команда покидает поле, набрав максимум очков. Рассмотрев матчи чемпионата мира с 1938 по 2006 год, они обнаружили, что, если только матч не кончается победой в три или четыре гола, нельзя быть полностью уверенным в том, что победит лучшая команда.
Затем Скиннер и Фриман пошли дальше. Они задали вопрос: какова вероятность того, что результат матча достоверно говорит о мастерстве обеих сторон? Если результаты идут бок о бок с мастерством, то мы бы навряд ли услышали о том, что мы называем «непереходным триплетом». То есть если бы в трех последовательных матчах «Ювентус», например, играл с «Ромой» и победил, затем «Рома» играла с «Удинезе» и победила, то затем «Удинезе» не должна была в свою очередь победить «Ювентус», так как мы уже выяснили, что «Ювентус» лучше «Ромы», а «Рома» лучше «Удинезе».
Но Скиннер и Фриман выяснили, что эти непереходные триплеты совсем не так редки, как должны были бы быть. Они отчасти приписывали это сравнительно небольшой разнице в мастерстве: «Ювентус», «Рому» и «Удинезе» разделяет лишь небольшой отрыв. Все было бы по-другому, если бы «Ювентус» играл с детской командой клуба «Удинезе» или местной деревенской командой. Про́пасть в уровнях мастерства сделала бы футбольные «ошибки», когда слабая команда побеждает сильную, намного менее вероятными.
Когда Скиннер и Фриман рассмотрели игры чемпионата мира, они обнаружили 355 триплетов из команд, играющих друг с другом, в 147 из которых не было ни одного матча, окончившегося вничью. Из этих 147 триплетов 17 были непереходными. Это 12 процентов, кажется, не так уж и много, если не учитывать того, что можно было бы ожидать, что 25 процентов триплетов будут непереходными при условии, что результаты всех матчей зависели бы исключительно от удачи.
Проще говоря, данные Скиннера и Фримана предполагают, что исход половины всех матчей чемпионата мира зависит от удачи, а не от мастерства. Лучшая команда побеждает только в половине случаев. Результаты футбола напоминают бросание монеты.
Другие ученые поддержали этот вывод. Дэвид Шпигельхалтер, профессор общественного понимания рисков Кембриджского университета, решил разобраться, действительно ли итоговое место команд в Премьер-лиге сезона-2006/07 отражало их «настоящую» силу16. Он хотел узнать, является ли чемпион сезона «Манчестер юнайтед» действительно лучшей командой и на самом ли деле клубы, вылетевшие из лиги («Уотфорд», «Чарльтон Атлетик» и «Шеффилд юнайтед»), обладали тремя худшими командами в лиге.
Чтобы найти ответ, Шпигельхалтеру надо было выяснить, какое количество разниц в набранных очках в турнирной таблице на финише сезона в лиге можно объяснить только удачей. Данные за прошлые годы показывают, что 48 процентов матчей являются победами на своем поле, 26 процентов оканчиваются ничьей и 26 процентов – победами на чужом поле. Шпигельхалтер назвал это законом 48/26/26. Если мы признаем, что команды не различаются уровнем мастерства, то можем вычислить результаты всех матчей сезона в соответствии с законом 48/26/26.
В этой воображаемой турнирной таблице лиги состязания на выход в Лигу чемпионов и на переход в низшую лигу располагались более плотно, чем в настоящей таблице, это доказывает, что команды действительно отличаются мастерством. Но все же есть определенное количество разниц в финальном счете, которое можно объяснить только удачей. На самом деле, вычисления Шпигельхалтера позволяют предположить, что около половины набранных очков можно приписать улыбке судьбы17.
Он обнаружил, что среди всех двадцати команд Премьер-лиги того сезона только «Манчестер юнайтед» и «Челси» могли уверенно занимать места в верхней половине таблицы, их шансы являться лучшей командой равнялись, соответственно, 53 и 31 процентам. Если говорить о нижней части таблицы, он мог быть на 77 процентов уверен в том, что «Уотфорд» был худшей командой, но для «Шеффилд юнайтед» эта уверенность составляла всего 30 процентов. Это почти не отличало ее от «Уигана» или «Фулхэма», а обе команды в тот год сохранили место в высшей лиге. Они были ничуть не лучше «Шеффилда», просто им больше повезло.
Дата добавления: 2018-10-26; просмотров: 260; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
