Марковские случайные процессы с непрерывным временем

⇐ ПредыдущаяСтр 2 из 2

Итак, снова модель Марковского процесса представим в виде графа, в котором состояния (вершины) связаны между собой связями (переходами из i-го состояния в j-е состояние), см. рис. 3.1..

Рис. 3.1. Пример графа Марковского процесса с непрерывным временем

Теперь каждый переход характеризуется плотностью вероятности перехода λ_ij. По определению:

При этом плотность понимают как распределение вероятности во времени.

Переход из i-го состояния в j-е происходит в случайные моменты времени, которые определяются интенсивностью перехода λ_ij.

К интенсивности переходов (здесь это понятие совпадает по смыслу с распределением плотности вероятности по времени t) переходят, когда процесс непрерывный, то есть, распределен во времени.

Зная интенсивность λ_ij появления событий, порождаемых потоком, можно сымитировать случайный интервал между двумя событиями в этом потоке.

где τ_ij — интервал времени между нахождением системы в i-ом и j-ом состоянии.

Далее, очевидно, система из любого i-го состояния может перейти в одно из нескольких состояний j, j + 1, j + 2, …, связанных с ним переходами λ_ij, λ_ij_{+ 1}, λ_ij_{+ 2}, ….

В j-е состояние она перейдет через τ_ij; в (j + 1)-е состояние она перейдет через τ_ij_{+ 1}; в (j + 2)-е состояние она перейдет через τ_ij_{+ 2} и т. д.

Ясно, что система может перейти из i-го состояния только в одно из этих состояний, причем в то, переход в которое наступит раньше.

Поэтому из последовательности времен: τ_ij, τ_ij_{+ 1}, τ_ij_{+ 2} и т. д. надо выбрать минимальное и определить индекс j, указывающий, в какое именно состояние произойдет переход.

Рассмотрим пример. Моделирование работы станка. Промоделируем работу станка (см. рис. 3.2.), который может находиться в следующих состояниях: S₀ — станок исправен, свободен (простой); S₁ — станок исправен, занят (обработка); S₂ — станок исправен, замена инструмента (переналадка) λ₀₂ < λ₂₁; S₃ — станок неисправен, идет ремонт λ₁₃ < λ₃₀.

Зададим значения параметров λ, используя экспериментальные данные, получаемые в производственных условиях: λ₀₁ — поток на обработку (без переналадки); λ₁₀ — поток обслуживания; λ₁₃ — поток отказов оборудования; λ₃₀ — поток восстановлений.

Реализация будет иметь следующий вид (рис. 3.2.).

Рис. 3.2. Пример моделирования непрерывного марковского процесса с визуализацией на временной диаграмме (желтым цветом указаны запрещенные, синим — реализовавшиеся состояния)

В частности, из рис. 3.2. видно, что реализовавшаяся цепь выглядит так: S₀—S₁—S₀—… Переходы произошли в следующие моменты времени: T₀—T₁—T₂—T₃—…, где T₀ = 0, T₁ = τ₀₁, T₂ = τ₀₁ + τ₁₀.

Очень часто аппарат Марковских процессов используется при моделировании компьютерных игр

1.4. Цепь Маркова

случайный процесс марковский вероятность

Представим, что производится последовательность испытаний.

Определение. Цепью Маркова называют последовательность испытаний, в каждом из которых появляется одно и только одно из несовместных событий полной группы, причем условная вероятность того, что в 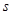-м испытании наступит событие , при условии, что в -м испытании наступило событие , не зависит от результатов предшествующих испытаний.

Например, если последовательность испытаний образует цепь Маркова и полная группа состоит из четырех несовместных событий , причем известно, что в шестом испытании появилось событие , то условная вероятность того, что в седьмом испытании наступит событие , не зависит от того, какие события появились в первом, втором, …, пятом испытаниях.

Заметим, что независимые испытания являются частным случаем цепи Маркова. Действительно, если испытания независимы, то появление некоторого определенного события в любом испытании не зависит от результатов ранее произведенных испытаний. Отсюда следует, что понятие цепи Маркова является обобщением понятия независимых испытаний.

Часто при изложении теории цепей Маркова придерживаются иной терминология и говорят о некоторой физической системе , которая в каждый момент времени находится в одном из состояний: , и меняет свое состояние только в отдельные моменты времени то есть система переходит из одного состояния в другое ( например из в ). Для цепей Маркова вероятность перейти в какое-либо состояние в момент 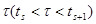зависит только от того, в каком состоянии система находилась в момент , и не изменяется от того, что становятся известными ее состояния в более ранние моменты. Так же в частности, после испытания система может остаться в том же состоянии («перейти» из состояния в состояние ).

Для иллюстрации рассмотрим пример.

Пример 1. Представим, что частица, находящаяся на прямой, движется по этой прямой под влиянием случайных толчков, происходящих в моменты . Частица может находиться в точках с целочисленными координатами: ; в точках и находятся отражающие стенки. Каждый толчок перемещает частицу вправо с вероятностью и влево с вероятностью 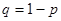, если только частица не находится у стенки. Если же частица находится у стенки, то любой толчок переводит ее на единицу внутрь промежутка между стенками. Здесь мы видим, что этот пример блуждания частицы представляет собой типичную цепь Маркова.

Таким образом, события называют состояниями системы, а испытания – изменениями ее состояний.

Дадим теперь определение цепи Маркова, используя новую терминологию.

Цепью Маркова с дискретным временем называют цепь, изменение состояний которой происходит в определенные фиксированные моменты времени.

Цепью Маркова с непрерывным временем называют цепь, изменение состояний которой происходит в любые случайные возможные моменты времени.

1.5 Однородная цепь Маркова. Переходные вероятности. Матрица перехода

Определение. Однородной называют цепь Маркова, если условная вероятность (переход из состояния в состоянии ) не зависит от номера испытания. Поэтому вместо пишут просто .

Пример 1. Случайное блуждание. Пусть на прямой в точке с целочисленной координатой находится материальная частица. В определенные моменты времени частица испытывает толчки. Под действием толчка частица с вероятностью смещается на единицу вправо и с вероятностью – на единицу влево. Ясно, что положение (координата) частицы после толчка зависит от того, где находилась частица после непосредственно предшествующего толчка, и не зависит от того, как она двигалась под действием остальных предшествующих толчков.

Таким образом, случайное блуждание − пример однородной цепи Маркова с дискретным временем.

Далее ограничимся элементами теории конечных однородных цепей Маркова.

Переходной вероятностью называют условную вероятность того, что из состояния (в котором система оказалась в результате некоторого испытания, безразлично какого номера) в итоге следующего испытания система перейдет в состояние .

Таким образом, в обозначении первый индекс указывает номер предшествующего, а второй − номер последующего состояния. Например, – вероятность перехода из второго состояния в третье.

Пусть число состояний конечно и равно .

Матрицей перехода системы называют матрицу, которая содержит все переходные вероятности этой системы:

Так как в каждой строке матрицы помещены вероятности событий (перехода из одного и того же состояния в любое возможное состояние ), которые образуют полную группу, то сумма вероятностей этих событий равна единице. Другими словами, сумма переходных вероятностей каждой строки матрицы перехода равна единице:

Приведем пример матрицы перехода системы, которая может находиться в трех состояниях 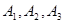; переход из состояния в состояние происходит по схеме однородной цепи Маркова; вероятности перехода задаются матрицей:

Здесь видим, что если система находилось в состоянии , то после изменения состояния за один шаг она с вероятностью 0,5 останется в этом же состоянии, с вероятностью 0,5 останется в этом же состоянии, с вероятностью 0,2 перейдет в состояние , то после перехода она может оказаться в состояниях ; перейти же из состояния в она не может. Последняя строка матрицы показывает нам, что из состояния перейти в любое из возможных состояний с одной и той же вероятностью 0,1.

На основе матрицы перехода системы можно построить так называемый граф состояний системы, его еще называют размеченный граф состояний. Это удобно для наглядного представления цепи. Порядок построения граф рассмотрим на примере.

Пример 2. По заданной матрице перехода построить граф состояний.

Т.к. матрица четвертого порядка, то, соответственно, система имеет 4 возможных состояния.

0,2 0,7

S2 0,4 S4

0,6 0,5

0,1 0,5

На графе не отмечаются вероятности перехода системы из одного состояния в то же самое. При рассмотрении конкретных систем удобно сначала построить граф состояний, затем определить вероятность переходов системы из одного состояния в то же самое (исходя из требования равенства единице суммы элементов строк матрицы), а потом составить матрицу переходов системы.

1.6 Равенство Маркова

Определение. Обозначим через вероятность того, что в результате шагов (испытаний) система перейдет из состояния в состояние . Например, – вероятность перехода за 10 шагов из второго состояния в пятое.

Подчеркнем, что при получим переходные вероятности

Поставим перед собой задачу: зная переходные вероятности найти вероятности перехода системы из состояния в состояние за шагов.

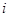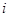С этой целью введем в рассмотрение промежуточное (между и ) состояние . Другими словами, будeм считать, что из первоначального состояния за шагов система перейдет в промежуточное состояние с вероятностью 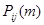, после чего за оставшиеся 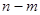шагов из промежуточного состояния она перейдет в конечное состояние с вероятностью .

По формуле полной вероятности, получим

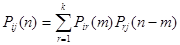. (1)

Эту формулу называют равенством Маркова.

Пояснение. Введем обозначения:

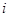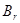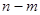– интересующее нас событие (за шагов система перейдет из начального состояния в конечное ), следовательно, ; − гипотезы( за шагов система перейдет из первоначального состояния в промежуточное состояние ), следовательно, − условная вероятность наступления при условии, что имела место гипотеза (за шагов система перейдет из промежуточного состояния в конечное ), следовательно,

По формуле полной вероятности,

( )

Или в принятых нами обозначениях

что совпадает с формулой Маркова (1).

Зная все переходные вероятности т.е зная матрицу перехода из состояния в состояние за один шаг, можно найти вероятности перехода из состояния в состояние за два шага, следовательно, и саму матрицу перехода 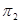; по известной матрице можно найти матрицу перехода из состояния в состояние за три шага, и т.д.

Действительно, положив в равенстве Маркова

Получим

Или

(2)

Таким образом, по формуле (2) можно найти все вероятности следовательно, и саму матрицу . Поскольку непосредственное использование формулы (2) оказывается утомительным, а матричное исчисление ведет к цели быстрее, напишу вытекающие из (2) соотношение в матричной форме:

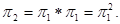
Положив в (1), аналогично получим

В общем случае

Теорема 1. При любых s, t

(3)

Доказательство. Вычислим вероятность по формуле полной вероятности ( ), положив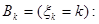

(4)

Из равенств

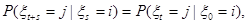
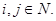
следует

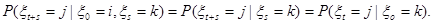
Отсюда из равенств (4) и

получим утверждение теоремы.

Определим матрицу В матричной записи (3) имеет вид

(5)

Так как то где − матрица вероятности перехода. Из (5) следует

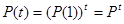(6)

Результаты, полученной в теории матриц, позволяют по формуле (6) вычислить и исследовать их поведение при

Пример 1. Задана матрица перехода Найти матрицу перехода

Решение. Воспользуемся формулой

Перемножив матрицы, окончательно получим: .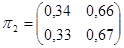

1.7 Стационарное распределение. Теорема о предельных вероятностях

Распределение вероятностей в произвольной момент времени 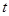можно найти, воспользовавшись формулой полной вероятности

(7)

Может оказаться, что не зависит от времени. Назовем стационарным распределением вектор 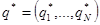, удовлетворяющий условиям

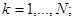
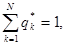
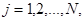(8)

где вероятности перехода.

Если в цепи Маркова то при любом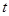

Это утверждение следует по индукции из (7) и (8).

Приведем формулировку теоремы о предельных вероятностях для одного важного класса цепей Маркова.

Теорема 1. Если при некотором >0 все элементы матрица положительны, то для любых , при

, (9)

где 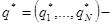стационарное распределение с а некоторая постоянная, удовлетворяющая неравенством 0<h<1.

Так как , то по условию теоремы из любого состояния можно попасть в любое за время с положительной вероятностью. Условия теоремы исключает цепи, являющиеся в некотором смысле периодическими.

Если выполнить условие теоремы 1, то вероятность того, что система находится в некотором состоянии , в пределе не зависит от начального распределение. Действительно, из (9) и (7) следует, что при любом начальном распределении ,

Рассмотрим несколько примеров цепи Маркова, которых условия теоремы 1, не выполнены. Нетрудно проверить, что такими примерами является примеры. В примере вероятности перехода имеют приделы, но эти приделы зависят от начального состояния. В частности, при 0< < ,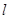

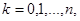
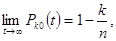
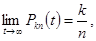
В других примеров приделы вероятностей при очевидно, не существуют.

Найдем стационарное распределение в примере 1. Нужно найти вектор удовлетворяющий условиям (8):

;

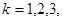
Отсюда, Таким образом, стационарное распределение существует, но не все координаты векторы положительны.

Для полиномиальной схемы были введены случайные величины, равные чесу исходов данного типа. Введем аналогичные величины для цепей Маркова. Пусть − число попадания системы в состояние за время . Тогда частота попаданий системы в состояние . Используя формулы (9), можно доказать, что при сближается с . Для этого нужно получить асимптотические формулы для и 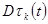и воспользоваться неравенством Чебышева. Приведем вывод формулы для . Представим в виде

(10)

где , если , и 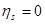в противном случае.

Так как ,то, воспользовавшись свойством математического ожидания и формулой (9), получим

Втрое слагаемое в правой части этого равенства в силу теоремы 1 является частной суммой сходящегося ряда. Положив , получим

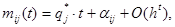
(11)

Поскольку

Из формулы (11), в частности, следует, что

при

Так же можно получить формулу для которая используется для вычисления дисперсии.

II глава. Марковские процессы

Рассмотрим систему, которую в любой момент времени можно описать одним из состояний, , для примера .

Через определенный промежуток времени система может изменить свое состояние или остаться в прежнем состоянии согласно вероятностям, указанным для данных состояний. Моменты времени, когда мы регистрируем состояние системы, обозначим как а состояние в момент времени мы обозначим . Полное описание рассмотренной выше системы должно содержать текущее состояние (в момент времени ) и последовательность всех предыдущих состояний, через которые прошла система. В отдельных случаях описание системы сводится к указанию текущего и предыдущего состояния, т.е.

(1.1)

Кроме того, мы также полагаем что процессы, протекающие в системе, не зависят от времени, о чем нам говорит правая часть формулы (1.1). Таким образом, систему можно описать матрицей вероятностей в виде

(1.2)

где - это вероятность перехода из состояния 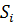в состояние в данный момент времени. Поскольку эти вероятности характеризуют случайный процесс, они имеют обычные свойства, т.е.

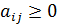
(1.3)

Описанный выше случайный процесс можно назвать открытой Марковской моделью, поскольку выходной сигнал модели - это последовательность состояний регистрируемых во времени. Каждое состояние соответствует определенному (наблюдаемому) событию.

Теперь рассмотрим простую Марковскую модель погоды, у которой будет всего три состояния. Предполагается, что мы один раз в день (например, в полдень), смотрим в окно и регистрируем в журнале текущее состояние погоды. Мы условились, что лишь одно из трех ниженазванных состояний в день мы записываем в журнал:

· Состояние №1: дождь (или снег)

· Состояние №2: пасмурно

· Состояние №3: ясно

Матрица вероятностей изменения погоды 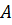имеет вид

(1.4)

Так как погода в первый день ( 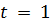) ясная (состояние 3), мы можем задать себе вопрос: какова вероятность (согласно нашей модели), что следующие 7 дней будет именно "ясно - ясно - ясно - дождь - дождь - ясно - пасмурно - ясно"? Точнее сказать, для данной последовательности состояний , где соответствует, мы хотим на основе данной модели определить вероятность наблюдения последовательности . Эта вероятность может быть выражена (и вычислена) следующим образом

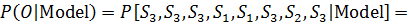
(1.5)

где - это вероятность того, что начальное состояние системы будет .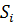

Есть и другой интересный вопрос, ответ на который нам даст эта модель: какова вероятность того, что модель сохранит свое состояние в течение ровно дней? Эта вероятность может быть вычислена как вероятность наблюдения следующей последовательности

дает модель, в которой

(1.6)

Величина - это вероятность того, что система будет находиться в состоянии ровно раз подряд. Соответственно, есть функция распределения вероятности для продолжительности пребывания системы в одном состоянии, которая является характеристикой сохранения состояния для Марковской цепи. Зная величины мы можем вычислить среднее время, в течение которого система сохранит свое состояние (используем формулу математического ожидания):

(1.7)

(1.8)

Ожидается, что солнечная погода вероятнее всего простоит дней, пасмурная - 2.5 дня, а вот дождливая погода, согласно нашей модели, вероятнее всего продержится 1.67 дня.

Размещено на Allbest.ru

Дата добавления: 2018-10-26; просмотров: 533; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!