Показатели центра распределения.
ЛАБОРАТОРНАЯ РАБОТА № 2
Обработка статистической совокупности. Определение графика распределения погрешности физической величины.
Цель работы: Построить вариационный ряд, полигон и гистограмму распределения. Провести предварительное определение закона распределения полученных результатов.
ОБЩИЕ СВЕДЕНИЯ
Для предварительного определения формы закона распределения полученных данных необходимо построить ряд распределения. Он может быть атрибутивным - при использовании качественных характеристик массива информации и вариационным – при использовании количественного массива. Для технических измерений применяется вариационный ряд, построенный в порядке уменьшения или увеличения значений (ранжированный ряд – представляет собой распределение полученного результата в определенной закономерности).
в порядке увеличения Х1 < Х2 < Х3 <… < Х n .
в порядке уменьшения Х1 > Х2 > Х3 > … > Х n .
Выделяется минимальное значение Хmin и максимальное Хmax, так же определяется число членов вариационного ряда.
Если число членов вариационного ряда велико, то для его изучения образуется интервальный ряд, который группируется по значениям интервала. Чаще всего длинна интервала выбирается постоянной и рассчитывается одним из двух способов
|
|
|
При одинаковой ширине интервалов и с заранее известным их количеством групп k (количество групп задается исходя из целей исследования).
, (1)
где Xmax, Xmin – максимальное и минимальное значение ряда распределения соответственно;
k – заранее известное количество групп.
При неизвестном числе групп расчет ширины интервала ведется в соответствии с правилом Старджесса, применяется при изменении значений, когда группировочный признак варьируется неравномерно в широких пределах.
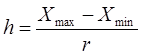, (2)
где h – ширина интервала;
r – количество групп.
r = 1 + 3.3 l о gN, (3)
где N – общее количество измерений.
Группировка с равными интервалами используется при значении коэффициента выравненности не менее кв > 0,1.
. (4)
Определяются границы интервалов.
Xmin + i (h) = Xmin+1 . (5)
Xmin+1 + i (h) = Xmin+2 и т.д.
В соответствии с которыми составляется вариационно–интервальный ряд и подсчитывается число попаданий в интервал.
Xmin ÷Xmin+1 < Xmin+1 ÷ Xmin+2 < Xmin+2 ÷ Xmin+3 <…
|
|
|
Для каждого интервала определяется число попаданий, сумма попаданий должна соответствовать общему числу измерений. Если число находится на границе интервала то оно учитывается только в один интервал.
Если число попаданий в интервал менее пяти, то соседние интервалы можно объеденить при условии, что оставшееся количество интервалов даст возможность оценить форму закона распределения. Полученный результат заносится в таблицу 2.
Таблица 2 - Вариационно-интервальный ряд распределения
| N | Интервалы | Хср | ni | рi | рнак | Fn |
| 1 | Xmin - Xmin+1 | |||||
| 2 | Xmin+1 - Xmin+2 | |||||
| 3 | Xmin+2 - Xmin+3 | |||||
| … | … | |||||
| итого | N | 1,00 |
Частость характеризует долю каждого значения в общем числе наблюдений.
, (6)
где ni – частота попадания в заданный интервал.
Накопленная частота – число вариант со значением менее Xi , так же называется накопленной частостью.
р нак = 
. (7)
|
|
|
Произведенные расчеты позволяют построить графические характеристики ряда распределения. Следуя из теоремы Бернулли при больших объемах выборки и с увеличением количества значений фактическое распределение приближается к теоретическому.
Гистограмма распределения (рис 1).
Гистограммой называется график, на котором ряд распределения выполняется в виде смежных столбцов. По оси абсцисс откладываются интервалы по оси ординат частоты. Площадь, заключенная под графиком пропорциональна числу измерений. Для гистограммы рекомендуется построение нечетного количества столбцов.
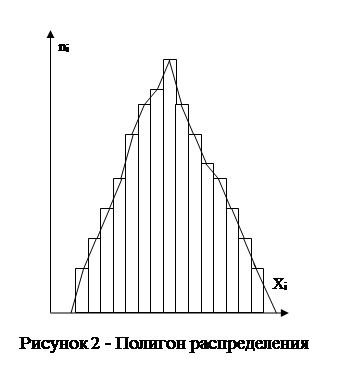Полигон распределения (рис 2).
Представляет собой ломанную кривую, соединяющую середины верхних оснований столбцов гистограммы. Более наглядно отражает график распределения. Площадь, заключенная под ломаной кривой должна быть равна единице.
Кумулятивная кривая (рис 3).
Представляет собой график статистической функции распределения. Представляет собой интегральную функцию распределения. Строится в соответствии кумулятивной частостью.
. (8)
По виду построенных зависимостей может быть оценен закон распределения. Кумулятивная частость суммируется с частостью предыдущего результата таким образом, что бы суммарная функция распределения равнялась 1,00.
|
|
|
Для более полной характеристики рассматриваемого массива информации необходимо определить ряд обобщающих факторов.
Показатели центра распределения.
Среднеарифметическая - для вариационно-интервального ряда применяется, если каждое значение варьируемого признака встречается в совокупности несколько раз. Для характеристики используют вес или частоту появления признака. Значение среднеарифметической взвешенной
. (9)
Мода (Мо) – величина, которая чаще всего встречается в статистическом распределении (наиболее вероятное значение). Если полученная функция имеет несколько максимумов, то мода будет иметь несколько значений, (функция называется полимодальной). Для определения моды и медианы необходимо выбрать модальный интервал. Модальным считается интервал, в который попало больше всего значений исследуемой величины.
, (10)
где Хо – нижняя граница модального интервала;
i - длинна интервала;
f1, f2, f3 – частоты предмодального, модального и послемодального интервала.
Графически мода определяется по гистограмме (рис.1).
Медиана (Ме) – среднее значение показателя в ранжированном ряду. Появление значения неизвестной величины одинаково вероятно как справа, так и слева от значения медианы, его значение должно быть серединой статистической совокупности.
(11)
где Хо – нижняя граница медианного интервала;
i - длинна медианного интервала;
- сумма частот ряда;
- сумма накопления частот до медианного интервала;
- частота медианного интервала.
Графически определяется по кумулятивной кривой (рис.3). Ось ординат для максимального значения делят пополам и опускают перпендикуляр на ось абсцисс.
Пример 1
В ходе измерения толщины листов электротехнической стали сердечника трансформатора при помощи микрометра получены следующие результаты: 0.25, 0.19, 0.26, 0.27, 0.25, 0.25, 0.24, 0.23, 0.27, 0.26, 0.24, 0.25, 0.23, 0.26, 0.,27, 0.24, 0.23, 0.25, 0.23, 0.26, 0.26, 0.25, 0.28, 0.24, 0.23, 0.25, 0.26, 0.24, 0.22, 0.22 мм. Выполнить первичный анализ статистической совокупности.
Решение
Определим повторяющиеся величины и частоту их повторения.
Таблица 3 - Повторяющиеся величины
| Xi | 0,19 | 0,22 | 0,23 | 0,24 | 0,25 | 0,26 | 0,27 | 0,28 |
| n | 1 | 2 | 5 | 5 | 7 | 6 | 3 | 1 |
Составим вариационный ряд в порядке возрастания
0,19 < 0,22< 0,23<0,24<0,25<0,26<0,27<0,28
В соответствии с расчетом коэффициента выравненности
длинна интервалов будет выбрана одинаковая.
Определим ширину интервала в соответствии с правилом Старджеса.
|
r = 1 + 3.3 lоg 30 = 5,85 
Определим границы интервалов.
Xmin + i (h) = 0,19+0,02 = 0,21 мм
X1 = 0,21+0,02 = 0,23 мм
X2 = 0,23+0,02 = 0,25 мм
X3 = 0,25+0,02 = 0,27 мм
X4 = 0,27+0,02 = 0,29 мм
Составляется вариационно–интервальный ряд и подсчитывается число попаданий в интервал.
0,19 - 0,21 < 0,21-0,23 < 0,23-0,25<0,25-0,27<0,27-0,29
Полученный результат заносится в таблицу 4 столбец 2.
Таблица 4 - Вариационно-интервальный ряд распределения
| N | Интервалы | Хср | ni | рi | рнак | Fn |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0,19 - 0,21 | 0,20 | 1 | 0,03 | 0,03 | 0,03 |
| 2 | 0,21-0,23 | 0,22 | 5 | 0,17 | 0,20 | 0,20 |
| 3 | 0,23-0,25 | 0,24 | 12 | 0,40 | 0,60 | 0,60 |
| 4 | 0,25-0,27 | 0,26 | 10 | 0,33 | 0,93 | 0,93 |
| 5 | 0,27-0,29 | 0,28 | 2 | 0,06 | 0,99 | 0,99 |
| итого | 30 | ≈ 1,00 | ≈ 1,00 |
Для полученного массива информации объединение первого и последнего интервала нецелесообразно, так как при недостаточном числе интервалов невозможно определить закон распределения.
Определим частость для каждого интервала.
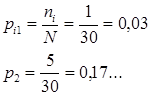
Накопление частоты заносим в таблицу.
рнак1 =0,03
рнак2 =0,03+0,17=0,2
рнак3=0,03+0,17+0,4=0,6…
Произведенные расчеты позволяют построить графические характеристики ряда распределения – полигон и гистограмму распределения (рис.4).
Для более полной характеристики построим кумулятивную кривую. Строится в соответствии кумулятивной частостью (рис.5).
В соответствии с формой полигона и гистограммы распределения предполагаемый закон распределения полученных результатов является нормальным.
Среднеарифметическое значение вариационно-интервального ряда
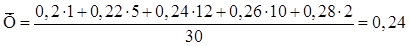мм
Расчетное значение представляет, среднюю толщину листа электротехнической стали сердечника трансформатора.
Мода
Мо = 
мм
Медиана
мм
Значение медианы соответствует среднему значению.
Вывод: в соответствии с полученными расчетными значениями наиболее близким к расчетному является нормальный закон распределения. Основные характеристики полученного распределения – среднеарифметическое значение 0,24 мм, мода – 0,25 мм, медиана - 0,24 мм.
ХОД РАБОТЫ
1. На основе полученных в лабораторной работе № 1 результатов измерений составьте вариационный ряд в порядке возрастания.
2. По полученному вариационному ряду разбейте результаты опытов на интервалы, для которых рассчитайте середину интервала, частость и накопление частоты.
3. Постройте гистограмму, полигон распределения и кумулятивную кривую. Сделайте вывод о законе распределения полученных результатов при помощи приложения 1.
4. Рассчитайте среднеарифметическое значение, моду и медиану распределения. Сделайте вывод по полученным результатам.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Охарактеризуйте свойства атрибутивного и вариационного ряда распределения.
2. При каких условиях применяется группировка с равными интервалами.
3. Какое понятие характеризует площадь, заключенная под кривой полигона распределения.
4. Какое понятие характеризует наиболее вероятное значение распределения.
5. В каких случаях допустимо объединять интервалы.
ПРИЛОЖЕНИЕ 1
| Законы распределения случайных погрешностей
| ||||||||||||||
| Гаусса | Равномерный | Симпсона | Экспоненциальный односторонний | Лапласа | ||||||||||
| 1 | 2 | 3 | 4 | 5 | ||||||||||
|
График плотности вероятности
| ||||||||||||||
| ||||||||||||||
|
Дифференциальная функция | ||||||||||||||
|
|
|
|
| ||||||||||
| 1 | 2 | 3 | 4 | 5 | ||||||||||
|
Интегральная функция
| ||||||||||||||
|
|
|
|
| ||||||||||
|
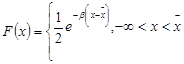
Энтропия
| ||||||||||||||
|
|
|
|
| ||||||||||
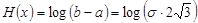
Дата добавления: 2018-10-26; просмотров: 522; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!