Электростатика. Постоянный ток. Электромагнетизм
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ДОНЕЦКОЙ НАРОДНОЙ РЕСПУБЛИКИ
ГОСУДАРСТВЕННОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ХАРЦЫЗСКИЙ ТЕХНОЛОГИЧЕСКИЙ ТЕХНИКУМ»
ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Утверждаю
зам. директора по УР
_______________ Г.В. Фаустова
«____» ___________ 2017 года
МЕТОДИЧЕСКОЕ ПОСОБИЕ
ДОМАШНЯЯ КОНТРОЛЬНАЯ РАБОТА
для специальности22.02.06 «Сварочное производство»
2017 г.
Методическое пособие ДКР по курсу Физика для специальности
22.02.06 «Сварочное производство» для студентов дневного отделения
Разработчик:
А.А. Розуванова – преподаватель, специалист высшей квалификационной категории Харцызского технологического техникума ГПОУ «ХТТ ДонНТУ»
Одобрена и рекомендована
с целью практического применения цикловой комиссией информационных технологий и физико-математических дисциплин
протокол № от « » 2017 г.
Председатель ЦК__________ Л.А. Полякова
Правила оформления контрольной работы
1. За время изучения курса общей физики студент должен выполнить одну контрольную работу в соответствии со своим вариантом.
2. Номер варианта соответствует порядковому номеру студента в учебном журнале группы.
3. Контрольная работа выполняется в отдельной школьной тетради и подписывается по следующему образцу:
|
|
|
Домашняя контрольная работа
по физике
Студента(ки) группы …….
заочного отделения ГПОУ ХТТ «ДонНТУ»
Фамилия И.О.
Номер варианта
4. Решение задач оформляется в соответствии с методическими указаниями к решению задач. Каждое задание оформляется с нового листа, условие задачи переписывается полностью.
6. Если контрольная работа не зачтена, то студент должен выполнить исправления в той же тетради и представить её на повторную проверку.
7. Срок сдачи контрольных работ определяется учебно-методическим планом специальности.
8. Зачтенная контрольная работа хранятся у преподавателя и студентам не возвращаются.
Методические указания к решению задач
Прежде чем приступить к решению задач какого-либо раздела, необходимо проработать теорию по этому разделу. Без знания теории нельзя рассчитывать на успешное решение даже простых задач. В решении большинства физических задач расчетного характера можно выделить четыре основных этапа:
1) анализ условия задачи, в котором необходимо дать схему или чертеж, поясняющий ее содержание (в тех случаях, когда это возможно);
2) составление уравнений, связывающих физические величины, характеризующие рассматриваемое явление с количественной стороны;
|
|
|
3) решение полученных уравнений относительно той или иной величины, считающейся в данной задаче неизвестной;
4) численный расчет и анализ полученного результата.
Рекомендуюю Вам при решении задач придерживаться следующей последовательности действий:
1. Полностью запишите условие задачи.
2. Сделайте краткую запись условия, выразите все данные в единицах СИ.
3. Выполните схематический чертёж (где это возможно), отражающий условия задачи и идею ее решения.
4. Запишите формулы, выражающие физические законы, применение которых необходимо для решения задачи выбранным способом. Сопровождайте решение задачи краткими, но исчерпывающими пояснениями. В результате получится одно или несколько уравнений, включающих в себя как заданные, так и неизвестные величины.
5. Прежде чем решать составленную систему уравнений, убедитесь в том, что число неизвестных равно числу уравнений, иначе система не будет иметь определенного решения.
Как правило, решать задачу следует в общем виде, т.е. надо выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи и взятых из таблиц. Получив ответ в виде алгебраической формулы или уравнения, проверьте, дает ли полученная формула единицу измерения искомой величины. Если при проверке единица измерения искомой величины не получается, то это означает, что в решении допущена ошибка. Убедившись в правильности наименования искомой величины нужно подставить в окончательную формулу числовые данные, выраженные в единицах одной системы.
|
|
|
Вычисления по расчетной формуле надо проводить с соблюдением правил приближенных вычислений. Как правило, окончательный ответ следует записывать как произведение десятичной дроби с одной значащей цифрой перед запятой на соответствующую степень десяти. Например, вместо 3520 надо записать 3,52·103, а вместо 0,0000129 записать 1,29·10−5 и т.п.
Основные формулы
Кинематика
Скорость и ускорение тела при прямолинейном движении в общем случае определяются формулами


В случае прямолинейного равномерного движения
υ =  = const, S = υ t , a = 0.
= const, S = υ t , a = 0.
В случае прямолинейного равнопеременного движения
υ = υ0 + at ,
S = υ0 t + 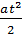 , a = const .
, a = const .
При криволинейном движении полное ускорение
|
|
|
a = aτ + an , 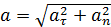
где aτ – тангенциальное (касательное ускорение), an – нормальное (центростростреительно) ускорение.


где υ – скорость движения, R – радиус кривизны траектории в данной точке,
ω – угловая скорость.
При вращательном движении в общем случае угловая скорость и угловое ускорение находятся по формулам
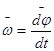
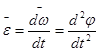
где dφ – угловое перемещение.
В случае равномерного вращательного движения угловая скорость
ω =  ,
,
где T – период вращения, v – частота вращения.
Угловая скорость ω и линейная скорость υ связаны соотношением
υ = ωR.
Тангенциальное и нормальное ускорения при вращательном движении
могут быть выражены в виде
aτ = εR, an =ω2R
Динамика
Импульс (количество движения) материальной точки массой m, движу-
щейся со скоростью υ,
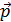 =
=  m .
m .
Второй закон Ньютона
 =
= 
где  – результирующая сил, действующих на материальную точку.
– результирующая сил, действующих на материальную точку.
Если масса тела m постоянна, то
 =
= 
где 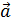 – ускорение, которое приобретает тело массой m под действием силы
– ускорение, которое приобретает тело массой m под действием силы  .
.
Закон сохранения импульса
 , если
, если 
Работа, совершаемая переменной силой
A = L∫ F(r)cos dr ,
где интегрирование ведется вдоль траектории, обозначаемой L.
Работа, совершаемая постоянной силой
A = FS cosα,
где α – угол между направлениями силы и перемещения.
Мгновенная мощность
N = 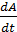 , N =
, N =  , N = F υ cosα .
, N = F υ cosα .
Кинетическая энергия тела, движущегося поступательно
Wк =  , или Wк =
, или Wк =  2
2
Потенциальная энергия:
а) упруго деформированной пружины
Wп =  ,
,
где k – жесткость пружины, x – абсолютная деформация.
б) тела, находящегося в однородном поле силы тяжести,
Wп = mgh,
где g – ускорение свободного падения, h – высота тела над уровнем, при-
нятым за нулевой (формула справедлива при условии h<< R, где R – радиус
Земли).
Закон сохранения механической энергии
W =Wк +Wп = const ,
если система замкнута и в ней действуют только консервативные силы.
Момент M силы F относительно произвольной оси вращения
M = F l ,
где l – плечо силы, т.е. кратчайшее расстояние от прямой, вдоль которой дейст-
вует сила, до оси вращения.
Момент инерции материальной точки относительно произвольной оси
вращения
J = mr 2,
где m – масса материальной точки, r – расстояние от оси вращения до точки.
Момент инерции некоторых тел массой m относительно оси z, проходя-
щей через центр масс:
а) стержня длиной l относительно оси, перпендикулярной стержню,
J =  ;
;
б) обруча (тонкостенного цилиндра) относительно оси, перпендикуляр-
ной плоскости обруча (совпадающей с осью цилиндра),
J = mR2,
где R – радиус обруча (цилиндра);
в) диска (однородного сплошного цилиндра) радиусом R относительно
оси, перпендикулярной плоскости диска,
J =  ;
;
Основной закон динамики вращательного движения
Mz =  =
= 
где Lz – проекция момента импульса на ось z, Mz – проекция момента сил,
приложенных к телу, на ось z.
Если момент инерции J = const, то
Mz =Jz  =Jzε
=Jzε
где ε – угловое ускорение, приобретенное телом под действием момента сил M.
Работа постоянного момента силы М, действующего на вращающееся тело
A = M φ,
где φ угол поворота тела.
Мгновенная мощность, развиваемая при вращении тела
N = Mω.
Кинетическая энергия вращающегося тела
Wк = 
где J момент инерции тела; ω – его угловая скорость.
Электростатика. Постоянный ток. Электромагнетизм
Основные формулы
Электростатика
Закон Кулона

где F – сила взаимодействия точечных зарядов q1 и q2; r – расстояние между зарядами; ε – диэлектрическая проницаемость; ε0 – электрическая постоянная.
 = 8,85*10-12
= 8,85*10-12 
Напряженность электрического поля E: 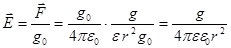
потенциал ϕ:  ,
,
где Wр – потенциальная энергия точечного положительного заряда q, находящегося в данной точке поля (при условии, что потенциальная энергия заряда, удаленного в бесконечность, равна нулю).
Линейная плотность заряда
τ = q/ l .
Поверхностная плотность заряда
σ = q/ s.
Напряженность электростатического поля, создаваемого бесконечной
прямой равномерно заряженной нитью или бесконечно длинным цилиндром:

где r – расстояние от нити или от цилиндра до точки, в которой определяется
напряженность.
Напряженность поля, создаваемого бесконечной равномерно заряженной
плоскостью:

Связь напряженности с потенциалом: а)  в случае однородного поля;
в случае однородного поля;
б) E = -  в случае поля, обладающего центральной или осевой симметрией.
в случае поля, обладающего центральной или осевой симметрией.
Работа сил поля по перемещению заряда q из точки с потенциалом φ1 в
точку с потенциалом φ2
A1−2 = q(φ1 − φ2).
Электроемкость

где ϕ – потенциал проводника (при условии, что в бесконечности потенциал
проводника принимается равным нулю); U – разность потенциалов пластин
конденсатора.
Электроемкость плоского конденсатора

где S – площадь пластины (одной) конденсатора, d – расстояние между пласти-
нами.
Электроемкость батареи конденсаторов:
а)  при последовательном соединении;
при последовательном соединении;
б) 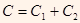 +…
+…  + С
+ С  при параллельном соединении,
при параллельном соединении,
где n– число конденсаторов в батарее.
Энергия электрического поля заряженного конденсатора:
 ;
; 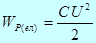 ;
; 
Объёмная плотность энергии электрического поля:
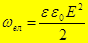
Постоянный электрический ток
Сила постоянного тока

где q – заряд (количество электричества), прошедший через поперечное сечение
проводника за время t.
Плотность электрического тока

где I – сила тока, S – площадь поперечного сечения проводника.
Сопротивление однородного проводника

где ρ – удельное электрическое сопротивление вещества проводника, l – его
длина, S – площадь поперечного сечения проводника.
Электрическая проводимость G проводника и удельная электрическая
проводимость вещества σ :


Зависимость удельного электрического сопротивления проводников от
температуры:
ρ = ρ0 (1+ αt) ,
где ρ и ρ0 – удельные сопротивления соответственно при t и 0°С; t – температу-
ра по шкале Цельсия; α – температурный коэффициент сопротивления.
Закон Ома для участка цепи:

Закон Ома для полной цепи:

ε– эдс источников тока, входящих в участок; U – напряжение на участке цепи; R – сопротивление внешней цепи , r - внутреннее сопротивление цепи.
Правила Кирхгофа.
Первое правило: алгебраическая сумма сил токов, сходящихся в узле, равна нулю.
Второе правило: в замкнутом контуре алгебраическая сумма напряжений на всех участках контура равна алгебраической сумме электродвижущих сил.
Работа, совершаемая электростатическим полем и сторонними силами в
участке цепи постоянного тока за время t,
А= І U 
Мощность тока

Закон Джоуля – Ленца
Q = I 2Rt ,
где Q – количество тепла, выделяющееся в цепи за время t. Закон Джоуля –
Ленца справедлив при условии, что участок цепи неподвижен и нем не совершаются химические превращения.
Дата добавления: 2018-09-23; просмотров: 167; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
