Деление без восстановления остатка

Прямой код

Сформулируем правила выполнения операций сложения и вычитания чисел со знаками (такие операции принято называть алгебраическими). Во-первых, алгебраическое вычитание всегда можно свести к алгебраическому сложению, изменив знак второго операнда. Далее следует сравнить знаки слагаемых. При одинаковых знаках складывают модули слагаемых и результату присваивают знак любого слагаемого (они одинаковые). Если знаки слагаемых разные, то из большего модуля слагаемого вычитают меньший модуль и присваивают результату знак слагаемого, имеющего больший модуль.

Рассмотрим случай сложения чисел с разными знаками. Он сводится к вычитанию модулей слагаемых, причем уменьшаемым должен стать больший модуль. Чтобы избежать дополнительной модульной операции сравнения, можно произвести "наугад" вычитание А-В . Признаком того, что |А| >|B|будет отсутствие заема из нулевого в первый разряд. Поскольку рассматривается случай разных знаков слагаемых, то при отсутствии заема значение знакового разряда разности определится как 0-1 = 1-0 = 1, а при наличии заема 0-1-1 = 1-0-1 = 0. Таким образом, если при вычитании а-в получим с₀=1, это будет означать, что |A|>|B|, и результату следует присвоить знак числа а (с₀ :=а₀). Если окажется с₀ =0, то |A|<|B|, и следует осуществить вычитание в-а, присвоив результату знак числа в (с₀ :=ь₀).

Почему обратный и дополнительный код:

При выполнении алгебраического сложения в прямом коде приходится, во-первых, не только складывать, но и вычитать двоичные коды; во-вторых, код знака результата формируется искусственно, т. е. знаковые разряды обрабатываются по правилам, отличным от правил обработки разрядов числа. Для устранения отмеченных недостатков в ЭВМ широко используются специальные представления двоичных чисел — т. н. обратный и дополнительный коды.

Сложение в обратном коде

1. а>0, в>0, а + в<1

2. а>0, в<0, а + в>0 (коррекция)

3. а>0, в<0, а + в<0

4. а<0, в<0, |а + в|<1 (коррекция)

Для выполнения алгебраического сложения двоичных чисел, представленных в обратном коде, достаточно, не анализируя соотношение знаков и модулей, произвести сложение чисел, включая знаковые разряды, по правилам двоичной арифметики, причем возникающий в знаковом разряде перенос должен быть добавлен к младшему разряду результата, осуществляя тем самым коррекцию предварительной суммы. Полученный код является алгебраической суммой слагаемых, представленной в обратном коде.

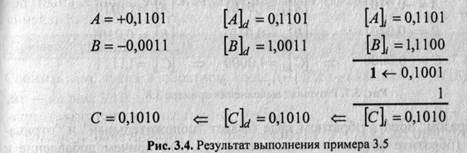
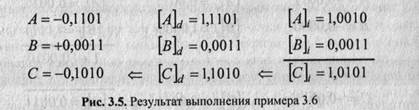
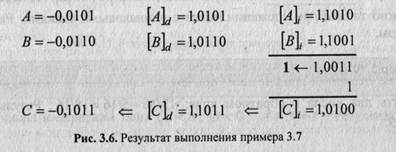
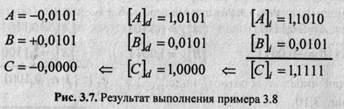
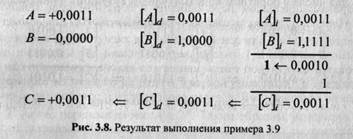
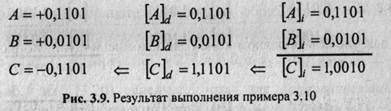
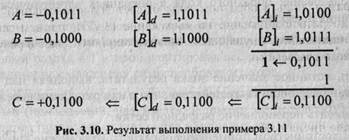
Таким образом, признаком переполнения в обратном коде можно считать знак результата, противоположный одинаковым знакам слагаемых:

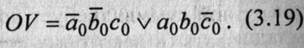
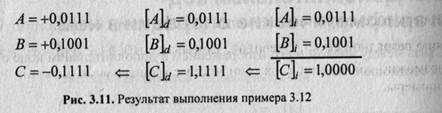
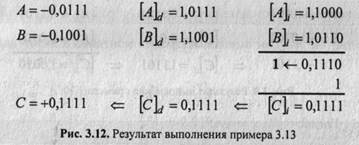
Итак, использование обратного кода в операциях алгебраического сложения/вычитания позволяет:

□ использовать только действие арифметического сложения двоичных кодов;

□ получать истинное значение знака результата, выполняя над знаковыми разрядами операндов те же действия, что и над разрядами чисел;

□ обнаруживать переполнение разрядной сетки.

Еще одним достоинством применения обратного кода можно считать простоту взаимного преобразования прямого и обратного кода.

Однако использование обратного кода имеет один существенный недостаток — коррекция предварительной суммы требует добавления единицы к ее младшему разряду и может вызвать (в некоторых случаях) распространение переноса по всему числу, что, в свою очередь, приводит к увеличению вдвое времени суммирования. Для преодоления этого недостатка можно использовать вместо обратного дополнительный код.

Дополнительный код

1. а>0, в>0, а + в<1

2. а>0, в<0, а + в>0 (коррекция)

3. а>0, в<0, а + в<0 (коррекция)

4. а<0, в<0, |а + в|<1 (коррекция)

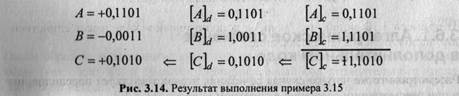
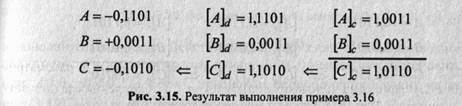
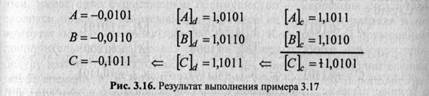
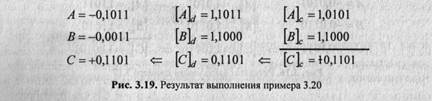
Сложить два числа в дополнительном коде: (-11/16) + (-5/16) = (-16/16). Результат — на рис. 3.20.

Переполнение по признакам выражения (3.19) не обнаружено! Однако результат операции — "отрицательный ноль", который не может использоваться

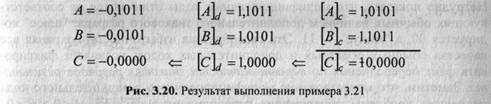
в дополнительном коде. Действительно, сложение в дополнительном коде любого числа с "отрицательным нулем" 1.00...0 меняет знак этого числа. Итак, при а<0, в<0, |а + в|=1 признаком переполнения служит не выражение (3.19), а код результата 1, 00...0.

Таким образом, значение признака переполнения в дополнительном коде можно получить в соответствии со следующим выражением:

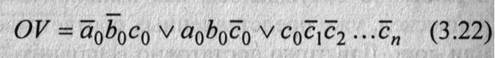
Подведем итоги. Применение дополнительного кода, по сравнению с обратным, имеет одно существенное преимущество — коррекция результата сводится просто к отбрасыванию переноса из знакового разряда и не требует дополнительных затрат времени. К недостаткам применения дополнительного кода можно отнести, во-первых, более сложную процедуру взаимного преобразования ПК <-» ДК, требующую дополнительных затрат времени, и, во-вторых, проблемы с обнаружением переполнения. Для того чтобы минимизировать влияние первого недостатка, данные в памяти часто хранят в дополнительном коде. В этом случае преобразования ПК <-> ДК выполняются относительно редко — только при вводе и выводе.

Алгебраическое сложение/вычитание

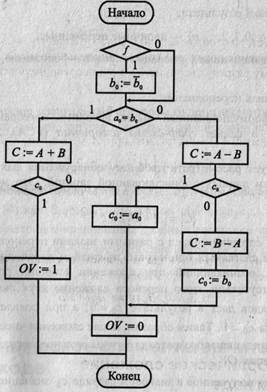
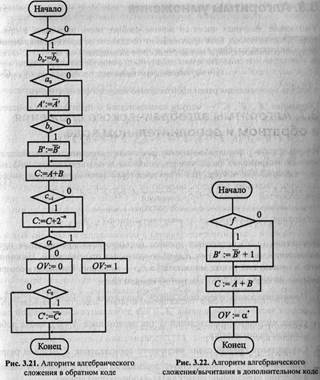
Где:

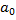□ , b ₀ — знаковые разряды слагаемых;

□ с₀ — код знака результата;

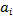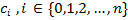□ , bj, — двоичные переменные;

□ f — тип выполняемой операции: f = 0 — сложение, f = 1 — вычитание;

□ OV — признак переполнения,

□ А' = 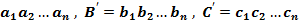—модули чисел;

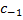□ — перенос из знакового разряда;

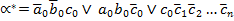□ — ситуации переполнения в дополнительном коде.

Умножение в прямом коде

Умножение двоичных чисел со знаком удобнее всего проводить в прямом коде. Действительно, знак произведения не зависит от соотношения величин модулей сомножителей, а зависит только от их знаков:

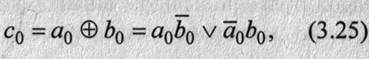
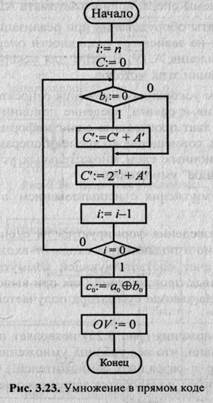
В изображенном на рис. 3.23 алгоритме, в отличие от алгоритмов сложения/вычитания, значение OV — 0 устанавливается безусловно. Действительно, А и В — дробные числа; очевидно при |A|<1 и |B|<1 всегда |А∙B|<1.

Алгоритмы деления

Знак частного, как и знак произведения, не зависит от соотношения модулей операндов и определяется в зависимости от знаков операндов по выражению (3.25). Поэтому рассмотрим сначала процесс деления модулей двоичных чисел.

Пусть А — делимое, В — делитель, С — частное, W — остаток.

Очевидно, при представлении чисел с фиксированной запятой как дробных, должно соблюдаться условие

|A|<|B| (3.29)

Сформулируем словесный алгоритм деления следующим образом:

1. Вычетают из делимого делитель. Если знак разности 0, то деление невозможно в силу нарушения условия (3.29), и следует, установив OV= 1, завершить операцию; иначе в разряд целой части частного записывают О (в конце операции в этот разряд помещается знак частного).

2. Так как остаток (разность А-В) оказался отрицательным, восстанавливают остаток путем добавления делителя к остатку.

3. Сдвигают восстановленный остаток влево на один разряд.

4. Вычитают из сдвинутого остатка делитель; если полученная разность положительна, то очередной цифрой частного становится 1, и следует перейти к п. 3; иначе очередная цифра частного — 0 и переходят к п. 2.

Пункты 2—4 повторяют столько раз, сколько цифр требуется получить в частном.

Деление дробных положительных чисел + (3/16):+(12/16) = +(1/4) = +(4/16) приведено на рис. 3.29.

Деление без восстановления остатка

Приведенный выше метод деления называется методом деления с восстановлением остатка. При получении отрицательного остатка на очередном шаге деления необходимо перед левым сдвигом восстановить остаток путем добавления к нему делителя. При этом для получения п -разрядного частного требуется в среднем 1,5и циклов сложения/вычитания.

Существует алгоритм деления без восстановления остатка, позволяющий корректировать отрицательные остатки без дополнительного цикла сложения. Рассмотрим действия, производимые с остатками в цикле деления в зависимости от полученного знака остатка (табл. 3.4).

Видно, что если на очередном шаге остаток получился отрицательный, его можно не восстанавливать, но на следующем шаге в этом случае нужно

вместо вычитания делителя из сдвинутого остатка добавить делитель к сдвинутому остатку.

Действительно, если W - В < 0, то следует восстановление остатка и сдвиг восстановленного остатка влево (его удвоение) 2-( W - B + В). На следующем шаге вычитаем делитель и получаем 2 W - B . Тот же результат может быть получен, если сдвинуть невосстановленный остаток, но на следующем шаге вместо вычитания произвести добавление делителя: 2{ W - B ) + B = 2 W -2 B + B = 2 W + B .

Дата добавления: 2018-09-22; просмотров: 1752; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!